
Решение.
Найдем
![]() .
Следовательно,
.
Следовательно,
![]() (ед.
работы).
(ед.
работы).
Угол
![]() между
между
![]() и
и
![]() находим
по формуле
находим
по формуле
![]() т.
е.
т.
е.
![]()
4. Евклидово пространство.
Скалярное произведение имеет следующие свойства:
1°. ху=ух – коммутативное свойство.
2°. х(у+z)=xy+xz – дистрибутивное свойство.
3°. (αх)у=α(ху) – для любого действительного числа α.
4°. хх>0, если х – ненулевой вектор, хх=0, если х – нулевой вектор.
Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным четырем свойствам (рассматриваемым как аксиомы), называется евклидовым пространством.
5.
Векторным
произведением
двух векторов
![]() и
и
![]() называется вектор
называется вектор
![]() ,
длина которого равна произведению длин
векторов
,
длина которого равна произведению длин
векторов
![]() и
и
![]() на
синус угла между ними и который направлен
перпендикулярно векторам
на
синус угла между ними и который направлен
перпендикулярно векторам
![]() и
и
![]() так, что векторы
так, что векторы
![]() ,
,![]() и
и
![]() образуют правую тройку векторов (рис.
3):
образуют правую тройку векторов (рис.
3):
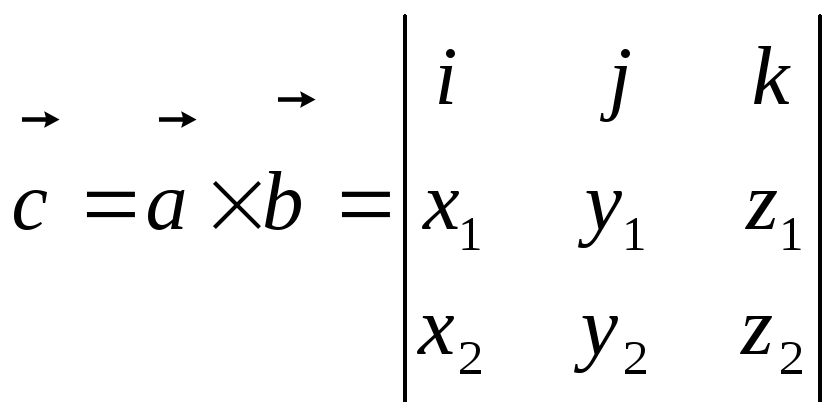 (4)
(4)
![]()
Геометрически
![]() равен площади S
параллелограмма, построенного на
векторах
равен площади S
параллелограмма, построенного на
векторах
![]() и
и
![]() :
:
![]()
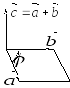
Рис. 3
Условие коллинеарности векторов:
Если
![]() ,
то
,
то
![]() (и наоборот), т. е.
(и наоборот), т. е.
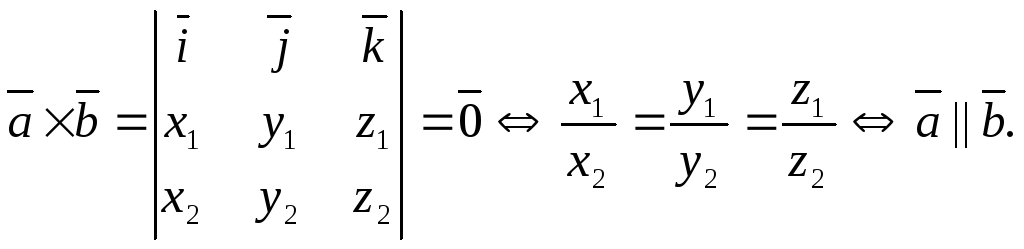
Некоторые приложения векторного произведения.
1.Определение момента силы относительно точки.
Пусть
в точке
![]() приложена
сила
приложена
сила
![]() и
пусть
и
пусть
![]() - некоторая точка пространства (рис.
4).
- некоторая точка пространства (рис.
4).
Из
курса физики известно, что моментом
силы
![]() относительно
точки
относительно
точки
![]() называется вектор
называется вектор
![]() ,
который
проходит через точку
,
который
проходит через точку
![]() и:
и:
1)
перпендикулярен плоскости, проходящей
через точки
![]()
2) численно равен произведению силы на плечо
![]()
3)
образует правую тройку с векторами
![]() и
и
![]() .
.
Значит,
![]() .
.
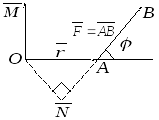
Рис.4
2.Нахождение линейной скорости вращения.
Скорость
![]() точки
точки
![]() твердого
тела, вращающегося с угловой скоростью
твердого
тела, вращающегося с угловой скоростью
![]() вокруг
неподвижной оси, определяется формулой
Эйлера
вокруг
неподвижной оси, определяется формулой
Эйлера
![]() ,
где
,
где
![]() ,
где
,
где
![]() —
некоторая неподвижная точка оси (рис.
5).
—
некоторая неподвижная точка оси (рис.
5).
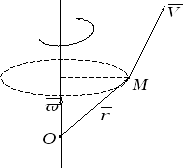
Рис.5
6.
Смешанным
произведением
трех векторов
![]() ,
,
![]() и
и
![]() называется число, равное
называется число, равное
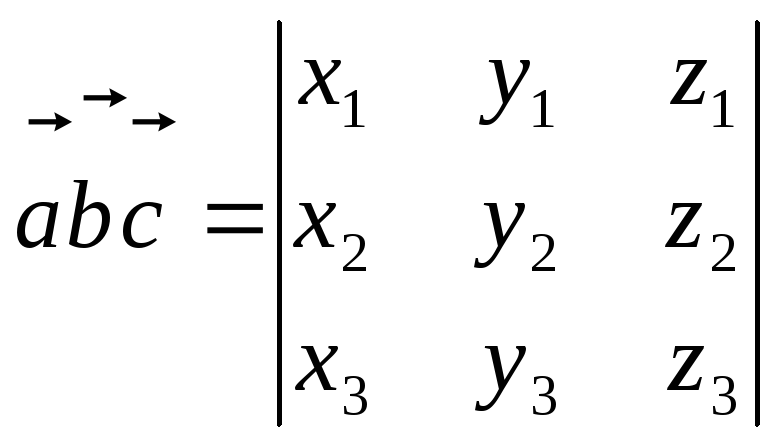 (5)
(5)
Модуль смешанного
произведения равен объему параллелепипеда,
построенного на векторах
![]() ,
,![]() и
и
![]() .
.
Условие компланарности векторов.
Векторы
![]() и
и
![]() компланарны тогда и только тогда, когда
их смешанное произведение равно нулю
при условии, что
компланарны тогда и только тогда, когда
их смешанное произведение равно нулю
при условии, что
![]() :
:
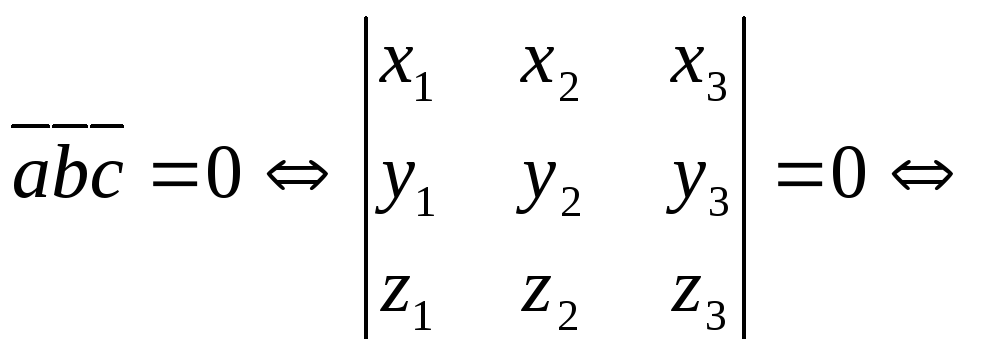 векторы
векторы
![]() компланарны.
компланарны.
Пример 4.
По координатам вершин пирамиды
![]() найти: 1) длины ребер
найти: 1) длины ребер
![]() и
и
![]() ;
2) угол между ребрами
;
2) угол между ребрами
![]() и
и
![]() ;
3) площадь грани
;
3) площадь грани
![]() ;
4) объем пирамиды.
;
4) объем пирамиды.
Решение.
1) Найдем векторы
![]() и
и
![]() :
:
![]()
![]() .
.
Найдем длины этих
векторов, т.е. длины ребер
![]() и
и
![]() :
:
![]()
![]() .
.
2) Скалярное
произведение векторов
![]() и
и
![]() найдем
по формуле (3):
найдем
по формуле (3):
![]() ,
,
косинус угла между этими векторами – по формуле:
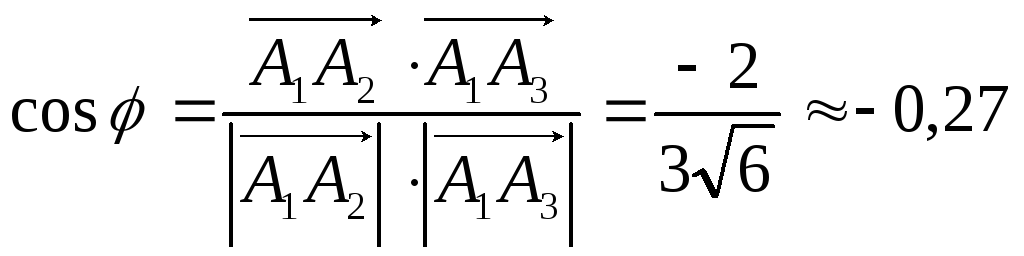 .
.
Следовательно, φ
– тупой угол, равный
![]() рад с точностью до 0,01. Это есть искомый
угол между ребрами
рад с точностью до 0,01. Это есть искомый
угол между ребрами
![]() и
и
![]() .
.
7. Вектор-столбец
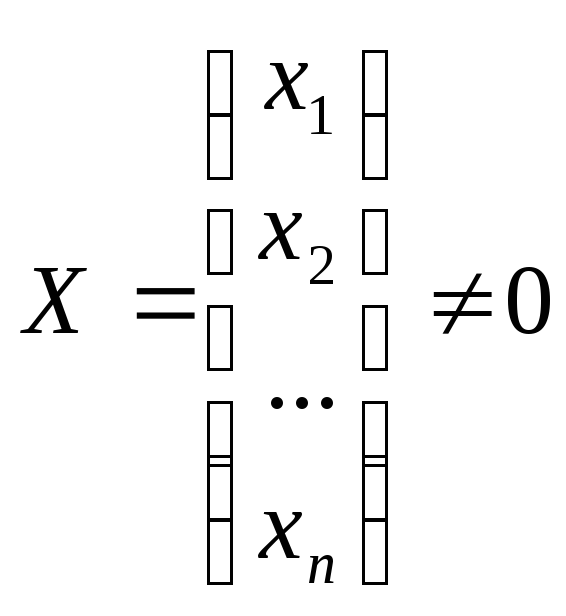
называется
собственным
вектором
квадратной матрицы А
n-го
порядка, соответствующим собственному
значению λ, если он удовлетворяет
матричному уравнению
![]() или
или
![]() .
.
Здесь Е
– единичная матрица n-го
порядка, 0 – нулевой вектор-столбец. При
условии, что вектор
![]() ,
получаем характеристическое
уравнение
для определения собственных значений
λ:
,
получаем характеристическое
уравнение
для определения собственных значений
λ:
![]() (6)
(6)
Координаты
собственного вектора
![]() ,
соответствующего собственному значению
,
соответствующего собственному значению
![]() ,
являются решением системы уравнений:
,
являются решением системы уравнений:
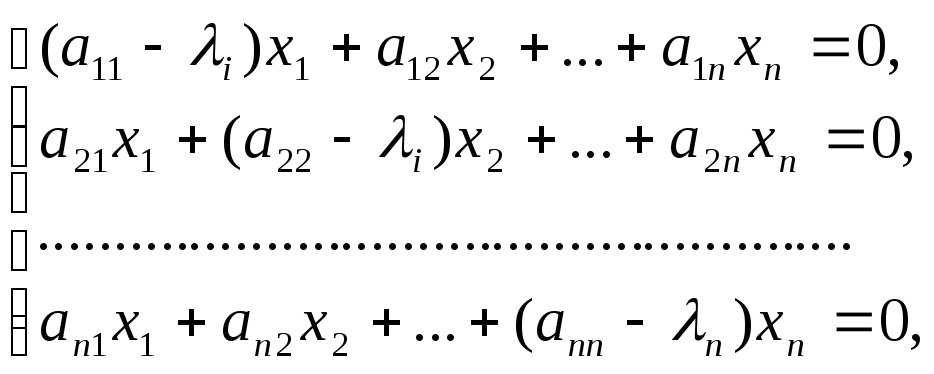 (7)
(7)
Собственный вектор определяется до постоянного множителя.
Пример 5. Определить собственные значения и собственные векторы матрицы
![]() .
.
