КРАТКИЙ КОНСПЕКТ ЛЕКЦИЙ

ПО ВЕКТОРНОЙ АЛГЕБРЕ

Краткий конспект лекций по векторной алгебре предназначен для самостоятельной работы студентов очной, очно-заочной и заочной форм обучения по дисциплине «Алгебра и геометрия». Содержит теоретический материал, примеры решения и контрольные вопросы по данному разделу высшей математики.

ОГЛАВЛЕНИЕ

Введение	4
Лекция 1. Векторы и их свойства	5
Лекция 2. Линейное пространство. Векторное пространство	7
Контрольные вопросы	13

ВВЕДЕНИЕ

Краткий конспект лекций по векторной алгебре предназначен для самостоятельной работы студентов очной, очно-заочной и заочной форм обучения по дисциплине «Алгебра и геометрия». Содержит теоретический материал, примеры решения и контрольные вопросы по данному разделу высшей математики.

Лекция 1

Векторы и их свойства

Контрольные вопросы:

1. Определение вектора.

2. Разложение вектора по базису.

3. Длина вектора. Направляющие косинусы.

4. Проекция вектора на заданное направление.

1. Вектором называется направленный отрезок.

Расстояние между началом и концом вектора называется его длиной (или модулем) и обозначается или .

Вектор, длина которого равна нулю, называется нулевым вектором и обозначается .

Вектор, длина которого равна единице, называется единичным вектором.

Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора .

Два ненулевых вектора называются противоположными, если они имеют одинаковую длину и противоположно направлены.

Два вектора называются коллинеарными, если они лежат на одной или параллельных прямых.

Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Два коллинеарных вектора и называются равными, если они сонаправлены и имеют равные длины.

2. Разложение вектора по базису. Если - орты координатных осей прямоугольной системы координат Oxyz, то любой вектор единственным образом можно представить в виде их суммы (линейной комбинации) с коэффициентами x, y, z, т.е. .

Коэффициенты x, y, z линейной комбинации называются координатами вектора в базисе .

Пусть система векторов , , является базисом, вектор – их линейная комбинация. Разложение любого вектора в базисе, если оно существует, является единственным. Значит,

.

Пример 1. Найти координаты вектора в базисе , ,, если , , .

Решение. Используя формулу , составим систему уравнений для нахождения координат вектора в базисе , ,.

или

Пример 2. Показать, что векторы , , образуют базис.

Решение. Составим определитель третьего порядка из координат данных векторов и найдем его.

,

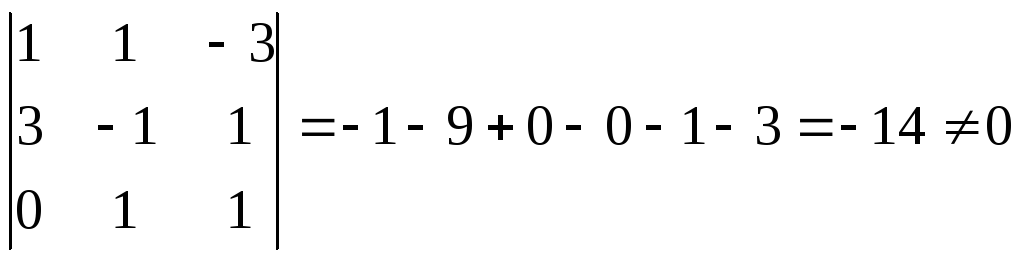следовательно, векторы линейно независимы, значит, они образуют базис.

3. Длина вектора определяется по формуле:

.

Пусть вектор образует с координатными осями Ox, Oy, Oz углы α, β, γ соответственно. Направление вектора определяется с помощью направляющих косинусов:

, , .

Направляющие косинусы связаны соотношением .

Пусть даны два вектора и . Тогда:

1) векторы и равны тогда и только тогда, когда равны их соответствующие координаты;

2) векторы и коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.

.

При сложении векторов их соответствующие координаты складываются, при вычитании – вычитаются, при умножении вектора на число – соответственно умножаются на это число:

,

.

4. Проекция вектора на заданное направление.

Проекцией вектора на ось и называется число, равное длине вектора(рис.1), взятой со знаком «плюс», если направление вектора совпадает с направлением оси и со знаком «минус» в противном случае.

Рис.1

Точки А₁, В₁ – это точки пересечения оси и с перпендикулярными ей плоскостями, проходящими через точки А и В.

Нахождение проекции вектора на направление, заданное вектором , может осуществляться по формуле, если и :

т.е. .

Лекция 2