Тема 6: Тепловые свойства тт. Электронный газ Ферми.

В кристаллах ионы образуют периодическую решётку, в которой свободно распространяются электронные волны.

Газ свободных, не взаимодействующих электронов, подчиняющихся принципу Паули, называют свободным электронным газом Ферми.

Последний заполненный уровень при температуре 0°К называется уровнем Ферми, а соответствующая ему энергия – энергией Ферми. Обозначается .

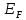В случае, если заполнены уровни вплоть до уровня Ферми, то говорят, что электронный газ полностью вырожден. Схематически это представляется.

Повышение температуры выше 0°К оказывает влияние прежде всего на электроны, находящиеся вблизи уровня Ферми. Они возбуждаются и переходят на соседние более высокие не занятые уровни. Говорят, что вырождение постепенно снимается. При повышении температуры распределение в виде ступеньки (при 0°К) вблизи Е = Е_F размывается, и возникает вероятность заселения электронами состояний, находящихся выше Е_F.

В 1926 году Ферми и независимо от него Дирак математически определили вид функции распределения электронов о энергиям, которая хорошо описывает поведение электронов как при низких температурах, так и при высоких:

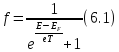
- распределение Ферми-Дирака.

Свойство функции f:

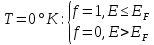
Поведение электронного газа в сильной степени зависит от соотношения между температурой кристалла и энергией Ферми. Различают 2 предельных случая:

1. Если 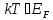, то газ является вырожденным.

2. Если (очень высокие температуры), то распределение Ферми-Дирака (6.1) переходит в классическое распределение, т.е. электроны ведут себя как классические частицы идеального газа. Вырождение электронного газа полностью снимается. ……..

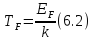
- температура Ферми, //////

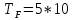Так как температура плавления металлов примерно ……, то ясно, что электронный газ остаётся вырожденным вплоть до температуры плавления, и его распределение очень мало отличается от распределения Ферми-Дирака при 0°К.

Лекция № от 25.11.2011

Тема 7: Полупроводники

Энергетические уровни примесных атомов в кристалле

Мы решали уравнение Шредингера для электронов, находящихся в кристалле с идеальной периодичностью, однако все реальные кристаллы имеют дефекты, в том числе примеси. Рассмотрим как изменяется энергетический спектр кристалла при наличии примесных атомов или дефектов. Присутствуют примеси, приводящие к тому, что на периодический потенциал решётки накладывается сильное возмущение . Это возмущение локализовано в малой области с центром, где располагается примесный атом. Таком образом, представим решение уравнения Шредингера в виде:

Решение этого уравнения осуществляется методом теории возмущений. Пи этом получается, что наложение возмущений на потенциал 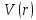приводит к отщеплению уровней от разрешённой зоны. При условии, что , где – среднее значение энергии возмущений в объёме , уровень поднимается выше «потолка валентной зоны», а при опускается ниже уровня, соответствующего дну зоны проводимости.

На рисунке: – локальный уровень.

Рассчитать положение локального уровня из общего уравнения Шредингера практически невозможно, даже если известен конкретный вид возмущений. Это происходит из-за того, что не известен точный вид периодического потенциала решётки . Однако, если воспользоваться понятием эффективной массы, которая учитывает период потенциала, то получим второе уравнение:

Где 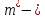эффективная масса.

Здесь отсутствует периодический потенциал, а эффективная масса может быть определена экспериментально. Данный метод решения уравнения Шредингера называется метод эффективной массы.