
- •1. Векторы, сложение и вычитание.
- •3.Скалярное произведение векторов, его свойства.
- •4.Правые и левые тройки и Векторное произведение
- •5.Смешанное произведение, его свойства.
- •6. Коллинеарные и компланарные векторы.
- •7. Прямая на плоскости.
- •8. Плоскость в пространстве.
- •9. Прямая в пространстве.
- •10. Эллипс, гипербола и парабола.
- •1. Эллипс
- •12. Подстановки.
- •13. Определить произвольного порядка.
- •14.Решение матричных ур-й
- •15. Теорема Кронекера-Капелли о разрешимости системы линейных уравнений.
- •16.Формулы Крамера
- •17.Ранг матрицы.Теорема о ранге матрицы и базисном миноре:
1. Векторы, сложение и вычитание.
Вектором-направленный
отрезокю.Вектор характеризуется 2
свойствами: длина и направление. Вектор
из начала координат в точку называется
радиус-вектор.Вектор
длина котор=1 наз-ся единич или ортом,
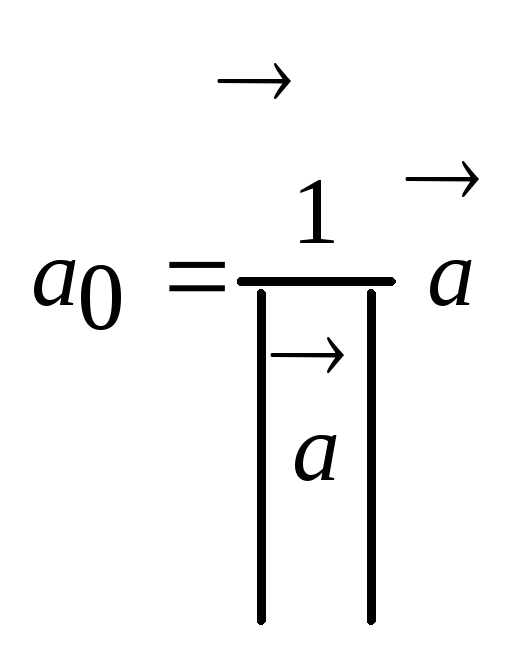
Свойства сложения: 1) (а+b)+c = a+ (b+c); 2) a + 0 = a; 3) a+(-a) =0; 4) a+b=b+a
Вычитание:а и b приложены к одной т., то р-ть этих векторов–вектор,с-й конец 2го с концом 1го. Пр-ние в-ра на число: α*а – вектор b=α*a :1)IbI=|α|*|a|,a и b сонапр, если α>0, или противополож., если α<0. b=0,если α=0 Св-во лин-ых оперц.:1)a+b=b+a 2(a+b)+c=a+(b+c) 3)сущ. 0:a+0=a 4)для люб. А сущ (-а):а+(-а)=0 5)α(а+b) = αa+αb 6)(α+β)a = αa+βa; 7) α(βa) = (αβ)a 8)1*а=а
2.ЛЗ и ЛНЗ.
С-ма в-ров
![]() линейн
прост-ва V
наз-ся ЛЗ,если сущ.числа а1,а2…аn
неравн одновр 0(а1^2+a2^2+…+an^2>0)т.ч.
лин.комб.=0
линейн
прост-ва V
наз-ся ЛЗ,если сущ.числа а1,а2…аn
неравн одновр 0(а1^2+a2^2+…+an^2>0)т.ч.
лин.комб.=0
![]()
С-ма в-ров
![]() линейн
прост-ва V
наз-ся ЛНЗ,если раве-во 0 их лин.комб.
возмж тольк в случ-е одноврем рав-ва 0
всех коэф.,а1,а2…аn.
линейн
прост-ва V
наз-ся ЛНЗ,если раве-во 0 их лин.комб.
возмж тольк в случ-е одноврем рав-ва 0
всех коэф.,а1,а2…аn.
Проекцией вектора
а на b
наз числ по ф-ле
![]()
Базисом на прямой наз-ся любо ненул вектор,на плоскости упорядочен пара неколинеар векторов,в пространстве упорядоч тройка некомпланар венкторов
3.Скалярное произведение векторов, его свойства.
Скаляр произвед
вектора а на вектор b
наз-ся число, равное (а, b)
= |a||b|*
cos(a,b).
Св-ва
скаляр
произвед:
1)
![]() ;
2) (a,b)=(b,a); 3)(αa,b) = α(a,b); 4)(a+b,c)= (a,c)+(b,c) 5)IaI=
;
2) (a,b)=(b,a); 3)(αa,b) = α(a,b); 4)(a+b,c)= (a,c)+(b,c) 5)IaI=![]()
![]()
4.Правые и левые тройки и Векторное произведение
Упорядоч тройка некомпланарн векторов наз-ся правой,если из конца 3го век-а перезод от 1го ко 2му происх-т против часовой стрелки, в др. случае тройка левая
Векторным произвед
вектора a
на вектор b
называется вектор c,
[a,b]=c,
такой что: 1)|с|=|a||b|sin(a,b);
2)![]() 3) a,
b,
c
– правая тройка. Хотя бы если один из
векторов равен 0, то векторное произведение
по определению равна 0. Св-ва
векторного
произведения:
1) [a,b]=-[b,a];
2) [αa,b]=α[a,b];
3) [a+b,c]
= [a,c]+[b,c];
4) a||b
<=>[a,b]
= 0; 5)Sпарал=|[a,b]|
3) a,
b,
c
– правая тройка. Хотя бы если один из
векторов равен 0, то векторное произведение
по определению равна 0. Св-ва
векторного
произведения:
1) [a,b]=-[b,a];
2) [αa,b]=α[a,b];
3) [a+b,c]
= [a,c]+[b,c];
4) a||b
<=>[a,b]
= 0; 5)Sпарал=|[a,b]|
Если векторы a
и b
заданы координатами (x1,
y1,
z1)
и (x2,
y2,
z2)
соответственно, то векторное произведение
находится по формуле
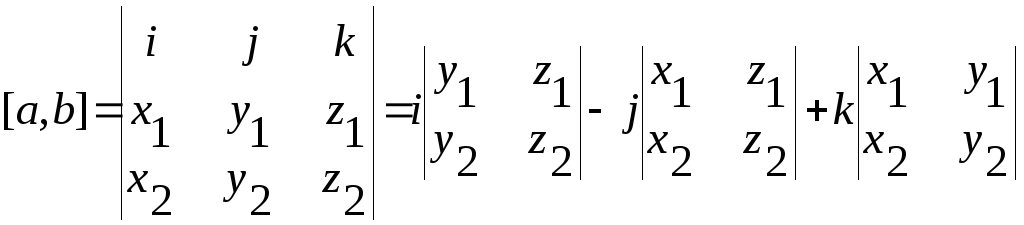
5.Смешанное произведение, его свойства.
Смешанным произвед векторов a, b, c называется число ([a,b],c), равное скаляр произвед векторного произвед векторов a и b на вектор c. смеш произв векторов = опр-лю 3его порядка в строках котор нах-ся корд перемнож векторов
Св-ва смеш произв.:
1)смеш произв линейно по каждому из своих 3ех аргументов
Геометрическое св-во см.пр:
2) если см.пр.V>0, то a, b, c – правая тройка., а если V<0, то левая; где V – объем параллелепипеда, построенного на 3 векторах. Vтетраэдра = 1/6 * V; 3) Три вектора a, b, c компланарны ([a,b],c)=0.
Основные св-ва смеш. пр:
(a,b,c)=(c,a,b)=(b,c,a)= -(b,a,c)=-(a,c,b)=-(c,b,a).
Если векторы a,
b,
c
заданы своими координатами (x1,
y1,z1),
(x2,
y2,
z2)
и (x3,
y3,z3)
соответственно, то смешанное произведение
может быть найдено по формуле:
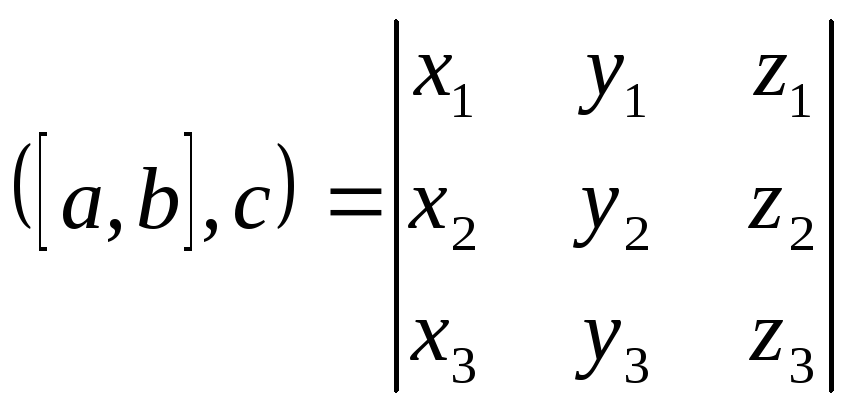
Двойное смеш произв
Выраж-е [а,[b,c]] наз-ся 2ым векторным произвед и представл собой вектор перпендик векторам [b,c] и а следов он и лежит в плос-ти вектров b и с
Утверждение
[a,[b,c]]=(a,c)b – (a,b)c
