
- •1. Понятие экстремума функции.
- •2. Формула Тейлора.
- •4. Теорема Коши.
- •5. Правило Лопиталя ( раскрытие неопределенностей).
- •10.Замена переменных в определенном интеграле
- •11. Свойства непрерывных функций, заданных на сегменте.
- •12. Определенный интеграл.
- •13. Понятие дифференцируемости.
- •14. Дифференциал.
- •15. Точки перегиба графика функции.
- •16.Вогнутость и выпуклость графика функции
- •17.Вычисление площади криволинейного сектора
- •18.Длина дуги
- •19. Теорема Ролля.
- •20. Теорема Лагранжа.
- •22. Точки разрыва функции одной переменной.
- •Классификация точек разрыва функции.
- •23. Neopredelennyi integral I pervoobraznaya
- •24. Cвойства непрерывных функций, заданных на сегменте
- •25. Интеграл Римана.
- •26. Существование первообразной непрерывной функции.
- •1) Докажем, что
- •27. Вычисление площади криволинейной трапеции.
- •28. Свойства непрерывных на отрезке функций.
- •29. Вычисление объема тела.
- •30. Вычисление площади поверхности тел вращения.
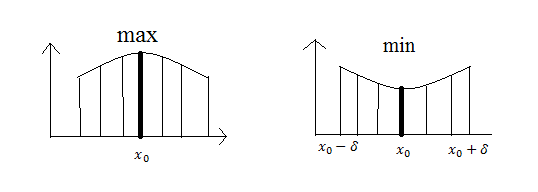
1. Понятие экстремума функции.
Экстремум
– максимальное или минимальное значение
функции на заданном множестве. Точка,
в которой достигается экстремум,
называется точкой экстремума ( – точка минимума;
– точка минимума;
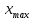 – точка максимума).
Точка
– точка максимума).
Точка
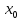 называется точкой строгого локального
max(min)
f(x),
еcли
называется точкой строгого локального
max(min)
f(x),
еcли

2. Формула Тейлора.


 многочлен
Тейлора для степени n
многочлен
Тейлора для степени n
 ,
,

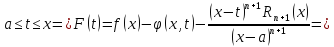
1) F(t) – дифференцируема и непрерывна [a,x]
2)
при

при
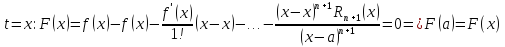
По
теореме Ролля в



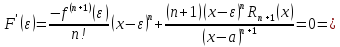
 остаточный
член в формуле Лагранжа
остаточный
член в формуле Лагранжа
3.
Формула Маклорена.
– Формула Тейлора при
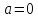

Остаточный член:
а) в форме Лагранжа
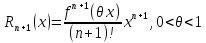
б) в форме Пеано

4. Теорема Коши.
Если
каждая из двух функций
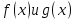 непрерывна на сегменте
непрерывна на сегменте
 и дифференцируема во всех внутренних
точках этого сегмента и если, кроме
того, производная
и дифференцируема во всех внутренних
точках этого сегмента и если, кроме
того, производная
 отлична от нуля всюду внутри сегмента
отлична от нуля всюду внутри сегмента
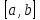 ,
то внутри этого сегмента найдется точка
,
то внутри этого сегмента найдется точка
 такая, что справедлива формула
такая, что справедлива формула
 (формула Коши)
(формула Коши)
Доказательство:
1)
докажем, что
 :
:
Предположим
что
 ,
то по теореме Ролля для
,
то по теореме Ролля для
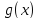 ,
внутри сегмента
,
внутри сегмента
 нашлась бы точка
нашлась бы точка
 такая, что
такая, что
 .
Это противоречит теореме
.
Это противоречит теореме .
.
2)
так как
 ,
то имеет место вспомогательная функция
,
то имеет место вспомогательная функция
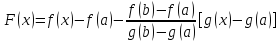
 – непрерывна
на
– непрерывна
на
 и дифференцируема
и дифференцируема

Имея
ввиду, что
 и
и


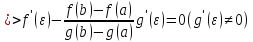
5. Правило Лопиталя ( раскрытие неопределенностей).
а)
Неопределенность вида

Т-1.
Пусть
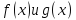 – определены и дифференцируемы в
некоторой окрестности точки
– определены и дифференцируемы в
некоторой окрестности точки
 ,
за исключением, быть может, самой точки
,
за исключением, быть может, самой точки
 ;
пусть, далее,
;
пусть, далее,
 если
существует
если
существует
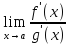 , то существует
, то существует
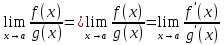
Доказательство:
пусть
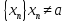
Доопределим
 в точке
в точке
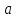

по
теореме Коши
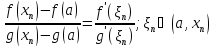
по
доопределению

так
как
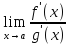 – существует
– существует

Теорема доказана. Замечание 1
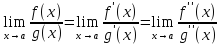
б)
Неопределенность вида

Аналогично
Т-1, но вместо
 заменяем
заменяем

в)
Неопределенности вида
 сводим к
сводим к

6.Необходимые условия локальных экстремумов
Теорема. Если f(x) имеет в точке x0 локальный экстремум и дифференцируема в этой точке, то f’(x0)=0.
Доказательство. Так как в точке x0 f(x) имеет локальный экстремум, то существует интервал (x0-ϭ,x0+ϭ) в котором f(x0) является min(max).
По теореме Ферма f(x0)=0. Ч.т.д.
7.Разрывы функции одной переменной первого рода
Точка
а называется точкой разрыва 1-го рода,
если в этой точке функция имеет конечные,
но не равные друг другу правое и левое
предельные
значения. Limx->a+0f(x) limx->a-0f(x).
limx->a-0f(x).
8.Разрывы функции одной переменной второго рода
Точка а называется точкой разрыва 2-го рода, если в этой точке функция не имеет по крайней мере одного из односторонних предельных значений или если хотя бы одно из односторонних предельных значений бесконечно.
9.Замена переменных в неопределенном интеграле
Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой.
Теорема.
Пусть функция x=ϕ(t)
имеет непрерывную производную ϕ’(t),
тогда
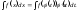
Доказательство.
Прибегнем к следующему свойству
первообразной функции: если F(x)–
первообразная для f(x),
то F(ϕ(t))
– первообразная для
 .
Следовательно, согласно определению
понятия неопределенного интеграла:
.
Следовательно, согласно определению
понятия неопределенного интеграла:
 или
или
 Но
в силу свойств неопределенного интеграла
Но
в силу свойств неопределенного интеграла
 или
или
 .
.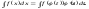 где разумеется
где разумеется
 .
.
