
- •Вариация в системе статистических показателей
- •Брянск издательство бгту
- •Предисловие
- •Введение
- •Глава 1. Измерение вариации
- •1.1. Понятие вариации. Абсолютные
- •Линейные
- •Квадратичные
- •1.2. Свойства показатеЛей вариации
- •1.3. Группировка данных и Расчет дисперсий
- •1.4. Правило сложения дисперсий
- •1.5. Взаимосвязи показателей вариации
- •1.6. Моделирование и вариационная оценка рядов распределения
- •1.7. Вариация в системе статистических показателей
- •Глава 2. Практическая реализация методов вычисления показателей вариации
- •2.1. Техника расчёта показателей вариации
- •2.2. Типовые примеры выполнения заданий
- •Глава 3. Вычисление показателей описательной статистики
- •3.1. Реализация Вычисления показателей описательной статистики с использованием табличного процессора excel
- •3.2. Описание технологии работы в режиме «оп»
- •3.3. Функции, связанные с режимом «оп»
- •Глава 4. Использование инструментария вариации
- •Вопросы к тесту
- •Список использованной и рекомендуемой литературы
- •Приложения
- •Вариация в системе статистических показателей
- •Темплан 2009 г., п. 30
1.5. Взаимосвязи показателей вариации
Между
показателями вариации (размахом R,
средней величиной
![]() ,
средним линейным
,
средним линейным
![]() и средним квадратическим отклонением
σ)
существуют определенные соотношения,
позволяющие судить о близости изучаемого
распределения к нормальному, контролировать
в некоторой степени результаты вычислений,
а также вычислять по уже имеющимся
показателям вариации неизвестные.
и средним квадратическим отклонением
σ)
существуют определенные соотношения,
позволяющие судить о близости изучаемого
распределения к нормальному, контролировать
в некоторой степени результаты вычислений,
а также вычислять по уже имеющимся
показателям вариации неизвестные.
Эти соотношения зависят от того, какому типу распределения вероятностей подчиняется совокупность исходных данных признака Х.
Так, между средним квадратическим отклонением σ и размахом вариации R существует следующая взаимосвязь:
![]() ,
откуда R
= 6 σ.
,
откуда R
= 6 σ.
Зная
![]() и σ
можно
представить размах вариации как R
=
и σ
можно
представить размах вариации как R
=
![]() ±
3 σ.
±
3 σ.
Эти соотношения вытекают из правила трёх сигм, по которому при нормальном распределении признака в совокупности его отклонение от средней арифметической по своей абсолютной величине не превышает утроенного среднего квадратического отклонения.
Другими словами, по закону нормального распределения вероятностей в интервал {±3σ} относительно среднего значения признака попадает 99,7% общего числа наблюдений (по правилу трех сигм). Размах вариации в этом случае ориентировочно соответствует шести средним квадратическим отклонениям. Но это справедливо, если наблюдений достаточно много. В противном случае вероятней всего, что они попадут в интервалы, близко примыкающие к среднему значению.
Рекомендуется оценивать среднее квадратическое отклонение следующим образом:
при числе наблюдений n = 5 делением размаха вариации на 2,30;
при n = 7 – делением размаха вариации на 2,70;
при n = 9 – делением размаха вариации на 3,0;
при n = 10 – делением размаха вариации на 3,10;
при n = 15 – делением размаха вариации на 3,50.
▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼▼
│►18
.
В
нашем примере для n
= 5 находим оценку среднеквадратического
отклонения:
(3600
– 2400) / 2,30 = 522 руб.
Она
достаточно близка к рассчитанному
значению. Для нормального распределения
величина среднего линейного отклонения
в пределе стремится к соотношению
В
нашем примере
После
корректировки дисперсии на малый размер
выборки получаем:
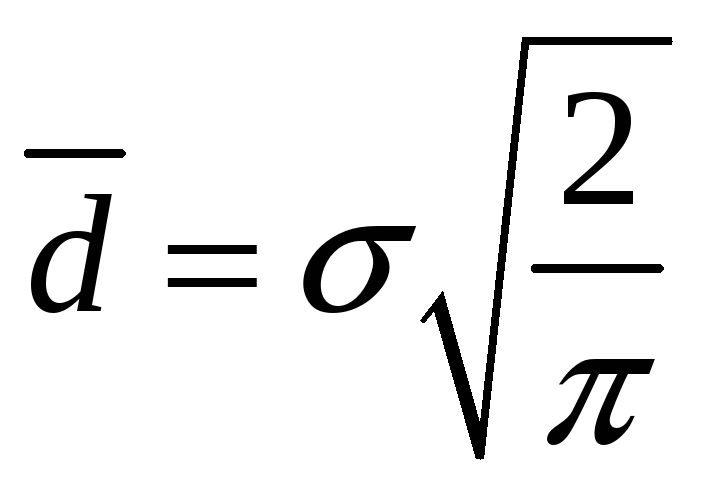 =
0,79788 σ.
=
0,79788 σ.![]() /σ
= 336/411,8 = 0,816.
/σ
= 336/411,8 = 0,816. ![]() ◄
◄
▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲▲
Если совокупность данных подчиняется закону равномерного распределения вероятностей, то
σ
=![]() .
.
Если первичные данные подчинены распределению вероятностей по закону Пуассона, то
σ2
=
![]() и т.д.
и т.д.
При
достаточно большом объёме совокупности
между средним квадратическим отклонением
σ
и средним
линейным отклонением
![]() существует следующее соотношение:
существует следующее соотношение:
σ
≈
1,25
![]() .
.
Отклонения индивидуальных значений признака от средней являются именованными числами и могут принимать различные значения. Их удобно выражать не в натуральном выражении, а в виде относительных величин.
Для
выражения отклонений индивидуальных
значений признака от средней или других
характеристик в условных стандартных
единицах отклонение х
-
![]() относят к σ
и
обозначают буквой t.
относят к σ
и
обозначают буквой t.
Полученное
отношение
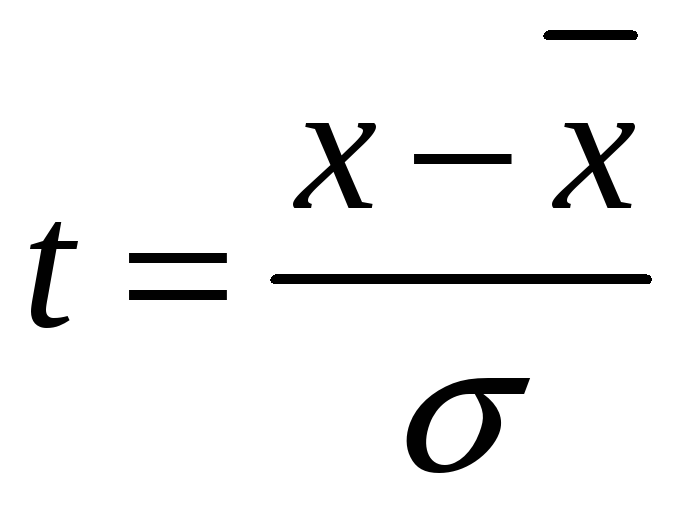 называется стандартизированным, или
нормированным отклонением. Оно
характеризует отклонение х
-
называется стандартизированным, или
нормированным отклонением. Оно
характеризует отклонение х
-
![]() ,
приходящееся на единицу σ.
,
приходящееся на единицу σ.
Отклонения, выраженные в долях среднеквадратического отклонения, изменяются в нормальном распределении в очень ограниченных пределах (практически от нуля до трёх). Кроме того, нормирование отклонений даёт возможность сопоставлять между собой отклонения, выраженные в различных единицах измерения. В этом их преимущество перед отклонениями, выраженными именованными числами.
Соотношения между показателями вариации особенно полезно учитывать на начальных стадиях анализа при проверке исходных данных, быстрой числовой оценке вариации, при выборе гипотезы о форме закона распределения и т.д.
