Глава 3. Вычисление показателей описательной статистики

с использованием программы «microsoft excel».

При анализе статистической информации используется перечень показателей, называемых показателями описательной статистики, которые можно разбить на четыре группы.

1. Показатели положения описывают расположение данных на числовой оси, например наименьшее и наибольшее значение признака в ряду; верхний и нижний квартили (ограничивают зону, в которую попадают 50% центральных элементов выборки); сведения о середине совокупности в виде средней арифметической, средней гармонической, медианы и т.п.

2. Показатели разброса показывают степень отклонения значений признаков совокупности относительно своего центра. Это дисперсия, среднеквадратическое отклонение, размах вариации (разность между максимальным и минимальным элементами), межквартильный размах (разность между верхней и нижней квартилью), эксцесс и т. п., характеризующие степень насыщенности формирования признаков относительно средних характеристик.

3. Показатели асимметрии характеризуют симметричность распределения признаков относительно средней (коэффициент асимметрии, медиана и т. п.).

4. Показатели, дающие закон распределения, позволяют выявить тенденцию распределения признаков (таблицы частот, таблицы частостей, полигоны, кумуляты, гистограммы).

На практике чаще всего используются следующие показатели: средняя арифметическая, медиана, дисперсия, стандартное отклонение. Однако для получения более точных и достоверных выводов необходимо учитывать и другие из перечисленных характеристик, а также обращать внимание на условия получения выборочных совокупностей. Наличие выбросов, т. е. грубых ошибочных наблюдений, может не только сильно исказить значения выборочных показателей (выборочного среднего, дисперсии, стандартного отклонения и т. д.), но и привести ко многим другим ошибочным выводам.

3.1. Реализация Вычисления показателей описательной статистики с использованием табличного процессора excel

Приведём справочную информацию по технологии работы в

режиме «Описательная статистика». Это может быть использовано, например, для генерации одномерного статистического отчета по основным показателям положения, разброса и асимметрии в некоторой совокупности.

В диалоговом окне режима «Описательная статистика» (рис. 6) должны быть заданы 8 параметров:

1. Входной интервал.

2. Группирование.

3. Метки в первой строке/Метки в первом столбце.

4. Выходной интервал/Новый рабочий лист/Новая рабочая книга.

5. Итоговая статистика – устанавливается в активное состояние (АС), если в выходном диапазоне необходимо получить по одному полю для каждого из следующих показателей описательной статистики:

• средняя арифметическая выборки (),

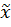• средняя ошибка выборки (),

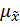• медиана (Me),

• мода (Mo),

• оценка стандартного отклонения по выборке (),

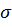• оценка дисперсии по выборке (D),

• оценка эксцесса по выборке (E_k),

• оценка коэффициента асимметрии по выборке (),

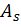• размах вариации выборки (R),

• минимальный и максимальный элементы выборки,

• сумма элементов выборки,

• число элементов в выборке,

• к-й наибольший и к-й наименьший элементы выборки,

• предельная ошибка выборки ().

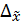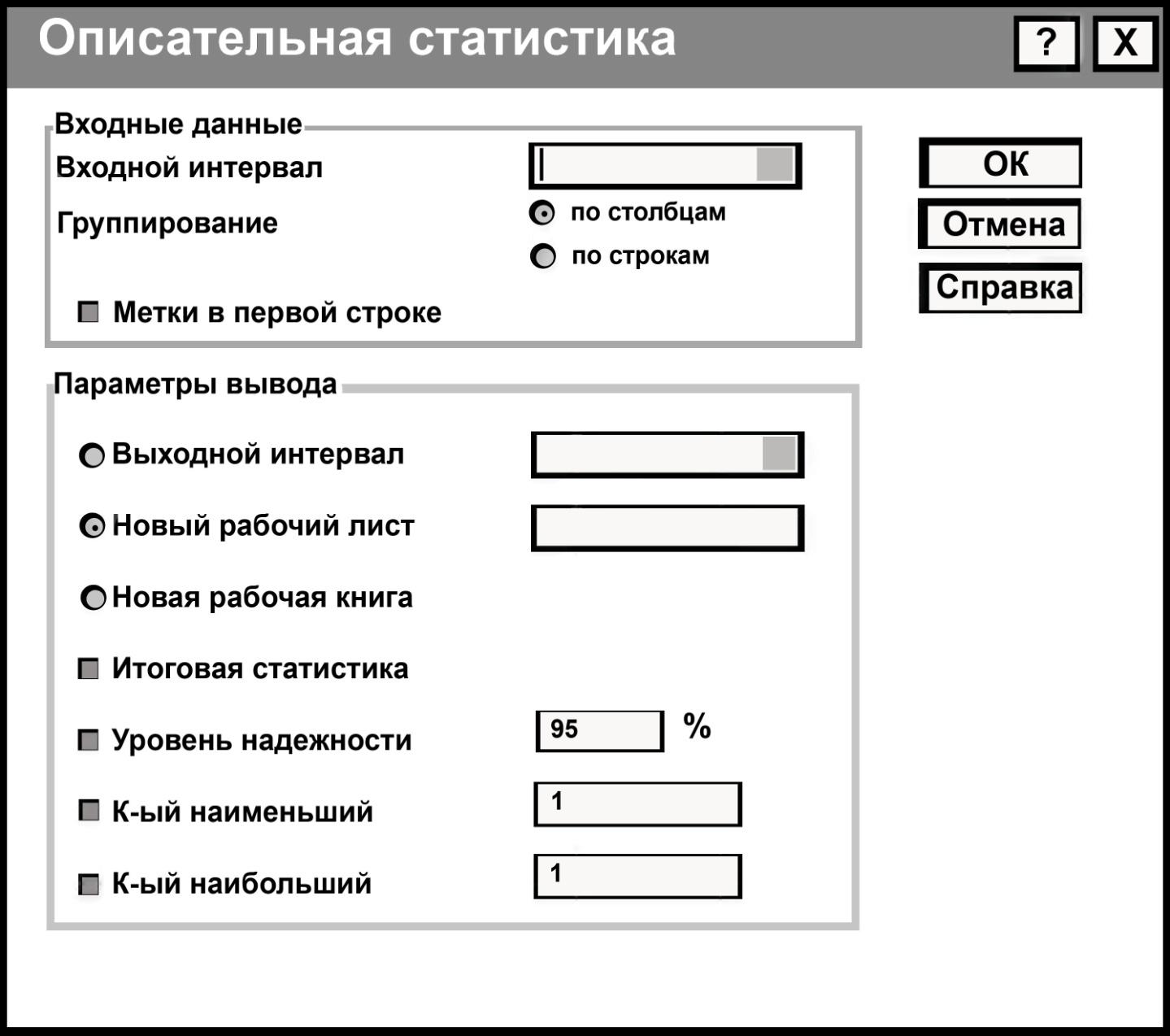
Рис. 6. Диалоговое окно режима «Описательная статистика»

6. Уровень надежности - устанавливается в АС, если в выходную таблицу необходимо включить строку для предельной ошибки выборки (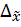) при установленном уровне надежности. В поле, против флажка, вводится требуемое значение уровня надежности (например, значение уровня надежности 95 % равносильно доверительной вероятности у = 0,95 или уровню значимости 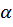= 0,05).

7. К-й наибольший - устанавливается в АС, если в выходную таблицу необходимо включить строку для k-го наибольшего (начиная с максимума х_тах) значения элемента выборки. В поле, расположенное напротив флажка, вводится число k. Если k = 1, то строка будет содержать максимальное значение элемента выборки.

8. К-й наименьший - устанавливается в АС, если в выходную таблицу необходимо включить строку для k-го наименьшего (начиная с минимума x_min) значения элемента выборки. В поле, расположенное напротив флажка, вводится число k. Если k = 1, то строка будет содержать минимальное значение элемента выборки.