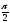- •2.Сформулируйте теорему Ролля.
- •Дайте определение интеграла с переменным верхним пределом. Докажите теорему Ньютона-Лейбница для определенного интервала.
- •5 Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами.
- •4. Дайте определение предела ф-ции двух переменных в точке. Имеет ли ф-ция предел в точке (0,0)?
- •1. Докажите ограниченность сходящейся последовательности.
- •2. Сформулируйте теорему Роля. В чем состоит ее геометрический смысл.
- •3. Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами.
- •6. Найти производную функции f(X,y) в точке м по заданному направлению:
- •1. Дайте определение предела последовательности. Может ли последовательность иметь два предела? Ответ обоснуйте.
- •2. Дайте определение дифференциала ф-ции в точке. Используя дифференциал, найдите приближенное значение для: ln 1,05.
1. Дайте определение предела последовательности. Может ли последовательность иметь два предела? Ответ обоснуйте.
1)
Число a
называют пределом последовательности
xn
 limn→∞xn=a,
если для любого положительного сколь
угодно малого числа ε>0
существует номер n0(ε)
такое, что начиная с этого номера все
члены последовательности xn
удовлетворяет неравенству 〡xn-a〡<ε.
limn→∞xn=a,
если для любого положительного сколь
угодно малого числа ε>0
существует номер n0(ε)
такое, что начиная с этого номера все
члены последовательности xn
удовлетворяет неравенству 〡xn-a〡<ε.
limn→∞xn=a
⇒
для любого ε>0
 no(ε)∈N:
no(ε)∈N:
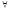 n≥no
⇒〡xn-a〡<ε.
n≥no
⇒〡xn-a〡<ε.
2) Допустим, что limn→∞xn=a и limn→∞xn=b, причем a≠b.
Пусть ε – такое малое положительное число, что Ua(ε)=(a-ε,a+ε) и Ub(ε)=(b-ε,b+ε) не имеют общих точек.
Ua(ε)∩Ub(ε) не является пустым множеством
limn→∞xn=a⇒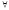 ε>0
ε>0
 n1∈N:
n1∈N:
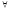 n≥n1⇒xn∈Ua(ε)
n≥n1⇒xn∈Ua(ε)
limn→∞xn=b⇒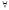 ε>0
ε>0
 n2∈N:
n2∈N:
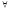 n≥n2⇒xn∈Ub(ε)
n≥n2⇒xn∈Ub(ε)
n0=max{n1,
n2}⇒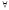 n≥n0⇒
n≥n0⇒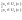 ⇒Ua(ε)∩
Ub(ε)≠∅
⇒Ua(ε)∩
Ub(ε)≠∅
Допущение неверно насчет a≠b.
2. Дайте определение дифференциала ф-ции в точке. Используя дифференциал, найдите приближенное значение для: ln 1,05.
Дифференциалом функции в точке х0 называется линейная относительно приращения аргумента часть приращения функции в этой точке, эквивалентная всему приращению.
df(х0)= f ′ (х0) ∆х; ∆х=dх; df(х0)= f ′ (х0) dх

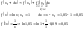
3. Дайте определение локального экстремума функции двух переменных. Имеет ли функция f(x,y) = xy² локальный экстремум в точке (0;0)? Ответ обоснуйте.
Точка Mo называется точкой локального максимума (минимума) функции f(x,y), если существует такая окрестность точки Mo, в которой для любой точки M(x,y) выполняется неравенство f(M)≤f(Mo) (f(M)≥ f(Mo))
Точки локального максимума и минимума называются точками локального экстремума или просто точками экстремума.
f(x,y)=xy2 Mo(0,0), M(Δx, Δy)
f(0,0)=0, f(M)= ΔxΔy2
f(M)-f(Mo)= ΔxΔy2
f(M)-f(Mo) ≥0 если Δx≥0
Mo(0,0) не является точкой
f(M)-f(Mo)≤0 если Δx≤0 локального экстремума (по определению)
4.
Найдите предел последовательности:
lim
( -4n)
=
-4n)
=
n→∞
=
(∞-∞) = lim
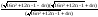 = lim
= lim
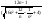 =
=
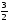
n→∞ n→∞
5.
Найдите определенный интеграл:
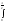
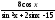 dx
=
dx
=
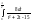 (=)
(=)
t = sinx
dt = cosxdx
|
x |
0 |
|
|
t |
0 |
1 |
(=)
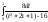 =
=
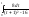 =
=
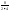 ln
ln
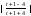
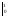
 =
ln
=
ln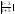
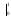 = ln
= ln
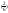 -
ln
-
ln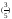 = ln (
= ln (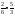 )
= ln(
)
= ln(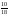 )
= ln
)
= ln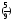
6. Найдите локальные экстремумы функции z(x,y) = -5x² + 4xy – 5y² - 18x -18y -7
-
Найдем стационарные точки:
f ‘(x) = -10x + 4y -18
f ‘ (y) = 4x -10y -18
*(2)
*(5)
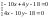
+
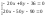
-42y=126
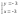
т. А (-3;-3) – стационарная точка
-
Проверим на наличие экстремумов:
f ‘’(xx) = -10
f ‘’(xy) = 4
f ‘’ (yy) = -10
d²f = -10 4

4 -10


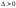
т. А (-3;-3) – max; f(max) = f (-3;-3) = 47
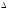
 <
0
<
0
7.
Решите разностное уравнение: x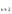 -3x
-3x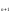 -
4x
-
4x =
-1
=
-1
-
x
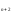 -3x
-3x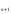 -
4x
-
4x =
0
=
0
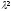 -3
-3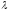 -
4 = 0
-
4 = 0
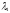 =
4;
=
4;
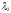 =
-1.
=
-1.
x =
c
=
c
 4
4 +
c
+
c
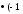 )
)

-
x
 =
Ax
=
Ax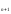 = A x
= A x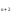 =
A-6A = -1, A =
=
A-6A = -1, A =
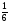 x
x =
=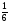 Вывод:
c
Вывод:
c
 4
4 +
c
+
c
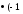 )
)
 +
+
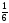 8.
Исследуйте
сходимость ряда:
8.
Исследуйте
сходимость ряда:
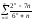 Сравним
с
Сравним
с
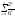 =
=
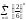 -
сходится
-
сходится
lim
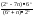 : 6
: 6
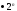 =
lim
=
lim
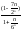 = 1 => ряды эквиваленты исходный ряд
сход.
= 1 => ряды эквиваленты исходный ряд
сход.
n→∞ n→∞
Скачано с сайта fa4you.ru