
- •2.Сформулируйте теорему Ролля.
- •Дайте определение интеграла с переменным верхним пределом. Докажите теорему Ньютона-Лейбница для определенного интервала.
- •5 Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами.
- •4. Дайте определение предела ф-ции двух переменных в точке. Имеет ли ф-ция предел в точке (0,0)?
- •1. Докажите ограниченность сходящейся последовательности.
- •2. Сформулируйте теорему Роля. В чем состоит ее геометрический смысл.
- •3. Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами.
- •6. Найти производную функции f(X,y) в точке м по заданному направлению:
- •1. Дайте определение предела последовательности. Может ли последовательность иметь два предела? Ответ обоснуйте.
- •2. Дайте определение дифференциала ф-ции в точке. Используя дифференциал, найдите приближенное значение для: ln 1,05.
1. Докажите ограниченность сходящейся последовательности.
Любая сходящаяся последовательность ограничена
limn→∞xn=a
⇒
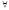 ε>0
ε>0
 no(ε)∈N:
no(ε)∈N:
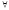 n≥n0⇒
xn∈Ua(ε)
n≥n0⇒
xn∈Ua(ε)
Начиная с n0 члены последовательности лежат в Ua(ε), конечное число начальных членов последовательности лежит вне Ua(ε). Очевидно, что найдется [c;d], который “накроет” как интервал (a-ε;a+ε), так и все начальные члены последовательности, не входящие в интервал.
2. Сформулируйте теорему Роля. В чем состоит ее геометрический смысл.
Теорема Ролля
Пусть
ф-ция
 непрерывна на отрезке [a;b],
дифференцируема на интервале (a;b)
и
непрерывна на отрезке [a;b],
дифференцируема на интервале (a;b)
и
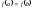 ,
то найдётся хотя бы одна точка
,
то найдётся хотя бы одна точка
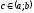 ,
в которой
,
в которой
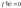 .
.
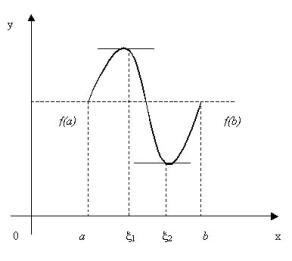
Геометрический смысл. Геометрический смысл теоремы Ролля: если функция, непрерывная на отрезке и дифференцируемая внутри ее, на концах этого отрезка принимает одинаковые значения, то хотя бы в одной внутренней точке этого отрезка касательная к графику функции параллельна оси Ох (Рис. 5.6.2).
3. Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами.
Если
для ряда с положительными членами
 существует такое число q<1,
что при всех n
(или, начиная с некоторого n)
выполняется неравенство
существует такое число q<1,
что при всех n
(или, начиная с некоторого n)
выполняется неравенство
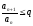 (*), то ряд сходится. Если же
(*), то ряд сходится. Если же
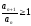 для всех или начиная с некоторого n,
то ряд расходится.
для всех или начиная с некоторого n,
то ряд расходится.
Доказательство.
Отбросив, если необходимо, несколько
первых членов ряда, можно считать, что
неравенство (*) выполняется для всех
п=1,
2, …Перепишем
это неравенство в виде
 .
Отсюда имеем
.
Отсюда имеем
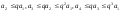 и т. д.; вообще, при любом п
справедливо
неравенство
и т. д.; вообще, при любом п
справедливо
неравенство
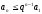 .
Это показывает, что члены ряда
.
Это показывает, что члены ряда
 .
Не превосходят соответствующих членов
бесконечной геометрической прогрессии
.
Не превосходят соответствующих членов
бесконечной геометрической прогрессии
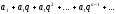 . Поскольку по условию
. Поскольку по условию
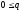 <1,
эта прогрессия сходится. В силу первого
признака сравнения сходится и данный
ряд. В случае, когда
<1,
эта прогрессия сходится. В силу первого
признака сравнения сходится и данный
ряд. В случае, когда
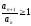 ,
имеем неравенство
,
имеем неравенство
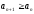 ,
т. е. члены ряда образуют неубывающую
последовательность, и поэтому не
выполняется необходимый признак
сходимости ряда, что доказывает теорему
полностью.
,
т. е. члены ряда образуют неубывающую
последовательность, и поэтому не
выполняется необходимый признак
сходимости ряда, что доказывает теорему
полностью.
4.
Найдите предел последовательности:
lim
(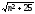 -
n)sin(n²+25)
(=)
-
n)sin(n²+25)
(=)
n→∞
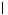 sin(n²+25)
sin(n²+25)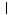 ≤1
=> sin
(n²+25)
– огранич.
≤1
=> sin
(n²+25)
– огранич.
Lim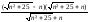 = lim
= lim
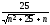 = 0 – бесконечно малое
= 0 – бесконечно малое
n→∞ n→∞
(=)
б.малое
 огр.
= 0.
огр.
= 0.
5.
Найти интеграл:
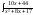 dx
=
dx
=
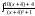 dx
=
dx
=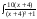 dx
+
dx
+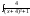 dx
(=)
dx
(=)
(x²+8x+16) – 16 + 17= (x+4) ² +1
t = (x+4) ² + 1
dt = 2(x+4)dx
(x+4)dx
=
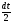
 dx
=
dx
=
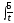 dt
= 5ln
dt
= 5ln
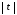 + C = 5ln
+ C = 5ln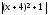 + C
+ C
(=)
5ln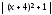 + 4arctg(x+4)
+ C
+ 4arctg(x+4)
+ C
6. Найти производную функции f(X,y) в точке м по заданному направлению:
f(x,y)
= 5x³
+3xy
– 2y³,
М(-1,1) по направлению вектора
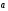 (3,4):
(3,4):
-
f ‘(x) = 15x² + 3y
-
f ‘(y) = 3x – 6y
 grad
(f) = ( 15x² + 3y; 3x – 6y)
grad
(f) = ( 15x² + 3y; 3x – 6y)
grad (f) = (18; -9)
2)
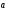 (3;4)
(3;4)
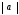 =
=
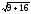 =
5
=
5
3)
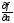 =
=
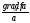 =
=
 =
=
 = 3
= 3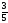
7.
Решите дифференциальное уравнение:
y’’
+ 2y’
– 3y
= (-12x
+4)e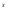
-
y’’ + 2y’ – 3y = 0
λ² + 2λ -3 = 0
λ = -3 λ = -1
y =
c
=
c
 e
e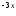 + c
+ c
 e
e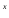
-
ŷ = (Ax + B)e
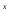
ŷ’
= Ae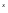 + e
+ e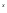 (Ax
+ B)
(Ax
+ B)
y”
= Ae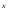 +
(Ax + B) e
+
(Ax + B) e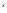 + Ae
+ Ae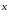 =
2Ae
=
2Ae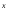 + (Ax + B)e
+ (Ax + B)e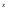
2Ae +
(Ax + B) e
+
(Ax + B) e + 2A e
+ 2A e + 2 e
+ 2 e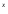 (Ax
+ B) – 3(Ax + B) e
(Ax
+ B) – 3(Ax + B) e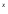 = (-12x + 4) e
= (-12x + 4) e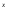
2A + (Ax + B) + 2A + 2 (Ax + B) – 3(Ax + B) = (-12x + 4)
4A = -12x + 4
4A = 4
A = 1
ŷ
= e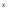
Вывод:
y = c
 e
e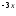 + c
+ c
 e
e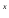 +
e
+
e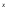
8.
Исследуйте сходимость ряда:
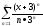 =
=
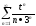
t = x+3
a =
=
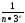 ;
a
;
a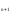 =
=
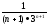
1)
R
= lim
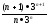 = 3
= 3
n→∞
2) Интервал сходимости: x принадл.: (-6;0)
-3<t<3
-3< x+3< 3
-6 < x < 0
-
x = -6:
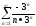 =
=
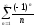 ;
;
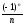 ↓ 0
по признаку Лейбница => ряд условно
сходится.
↓ 0
по признаку Лейбница => ряд условно
сходится.
x=
0:
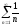 – расходится
– расходится
Область
сходимости: x
принадл.
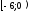
Билет 2
Билет №2
