АНАЛОГО-ЦИФРОВОЕ И ЦИФРО-АНАЛОГОВОЕ ПРЕОБРАЗОВАНИЕ СИГНАЛОВ

Аналого-цифровое преобразование (АЦП) сигналов является одной из важнейших составляющих цифровых телекоммуникационных систем. Аналого-цифровое преобразование обычно состоит из нескольких последовательных операций, как показано на рис. 1. Эти операции таковы. Дискретизация - представление непрерывного во времени сигнала рядом периодических дискретных значений. Возможность такого представления основана на известной теореме В.А. Котельникова, по которой функция, спектр которой сосредоточен в полосе частот до ω_в, полностью характеризуется своими мгновенными значениями, отсчитанными через интервалы времени ∆t = π/ω_в. Дискретизация нужна для временного разделения каналов, кроме того дискретизация позволяет применять синхронные микросхемы, работа которых происходит более четко. Квантование - округление мгновенных значений сигнала до ближайших разрешенных значений. Это важнейшая операция АЦП, которая, собственно и превращает аналоговый сигнал в цифровой.

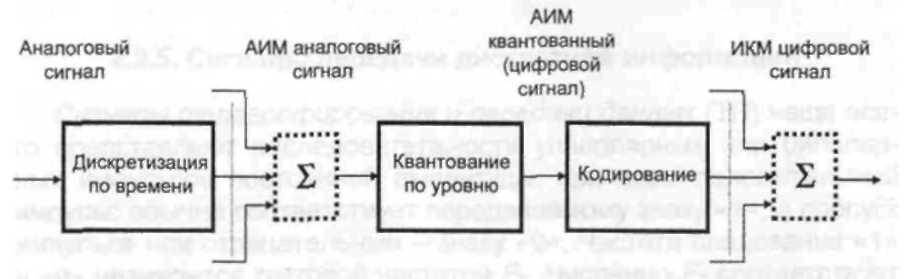
Рис. 1. Аналого-цифровое преобразование сигнала.

Квантование неизбежно сопровождается ошибкой квантования, не более шага квантования, т.е. расстояния между ближайшими разрешенными значениями. Уменьшая это расстояние, приходим к увеличению числа разрешенных значений и, как следствие, к необходимости повышать объем передаваемой информации при прочих равных условиях, например, за счет повышения скорости передачи.В оборудовании телекоммуникационных систем важнейшая операция квантование практически всегда совмещается с последующей - кодированием.

Кодирование - в теории электрической связи существует два понятия кодирования: в широком и узком смысле. В цифровых те- лекоммуникационных системах кодирование понимается в узком смысле, как переход от кода с высоким основанием к коду с низким основанием. Т.е. мгновенные значения, которые могут принимать достаточно много разрешенных значений (например, 256), заменя- ются комбинациями импульсов (кодовыми группами, состоящими, например, из 8 импульсов), которые имеют мало разрешенных зна- чений (минимум два). Это повышает помехоустойчивость сигнала и упрощает его обработку логическими устройствами.

Кроме указанных трех операций в цифровых телекоммуникационных системах осуществляется также мультиплексирование - объединение нескольких потоков (компонентных) в групповой поток (агрегатный).

В ЦТС прежних поколений объединение сигналов производили после дискретизации с тем, чтобы относительно сложный узел - кодер сделать групповым. В настоящее время, с повышением уровня цифровизации сетей связи, появилась тенденция выноса оборудования АЦП к абоненту, т.е., в конечном счете, получать групповой сигнал в результате объединения индивидуальных цифровых сигналов. Следует заметить, что операция мультиплексирования широко применяется в ЦТС и вне связи с аналого-цифровым преобразованием.

Очевидно, что операциям АЦП на передаче должны соответствовать обратные операции на приеме. Действительно, приходящий агрегатный поток демультиплексируется - разделяется на компонентные потоки, и декодируется. В результате декодирования восстанавливаются мгновенные значения сигнала, которые после прохождения фильтра нижних частот с частотой среза сов, превращаются в непрерывный исходный сигнал. Заметим, что восстановленный сигнал всегда отличается от исходного из-за операции квантования (сигнал восстанавливается не точно по исходным мгновенным значениям, а по округленным до разрешенных). Одна­ко, уменьшая шаги квантования, теоретически можно достигнуть сколь угодно малого отличия принятого сигнала от переданного.

Рассмотрим подробнее операции аналого-цифрового преобра­зования.

1. Дискретизация сигнала во времени

Дискретизация сигнала во времени реализуется посредством амплитудно-импульсной модуляции - модуляции импульсного пе­реносчика (АИМ). В качестве переносчика используется последова­тельность прямоугольных импульсов с более или менее стабиль­ной частотой следования f₀ (рис. 2,а). То, что в качестве перенос­чика применяются последовательности прямоугольных импульсов, определено простотой генерации и обработки таких последова­тельностей и не имеет Реальные импульсы имеют конечную длительность т_и. Удобно для характеристики таких последовательностей использовать ко­эффициент скважности (скважность) К_ск = Т₀ А_и, где Т₀ - период следования импульсов Т₀ = 1/ f₀. По Фурье, спектральный состав такой последовательности равен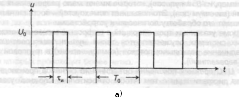

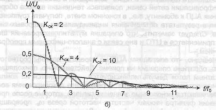
где

Как следует из формулы, спектр переносчика состоит из посто­янной составляющей и гармоник частоты f₀, причем гармоники с номерами, кратными К_ск, отсутствуют.

На рис. 2,6 показаны частотные составляющие импульсных последовательностей со скважностями 10, 4 и 2. На практике при­меняются последовательности со скважностями несколько десят­ков, что соответствует почти плоской форме огибающей спектра.

Простейший амплитудно-импульсный модулятор представляет собой ключ, срабатывающий при прохождении импульса переносчика и пропускающий при этом сигнал на свой выход (рис. 3,а,б). Такая амплитудно-импульсная модуляция называется АИМ-1 (АИМ первого рода). При АИМ-1 возникают проблемы дальнейшей обработки сиг­нала из-за неопределенности величины амплитуды импульса. По­этому применяется АИМ-2 (АИМ второго рода), при которой отсчет берется в какой-либо одной точке прохождения импульса, а затем это значение удерживается в течение некоторого времени.

На рис. З.в показан сигнал АИМ-2, у которого амплитуды им­пульсов соответствуют мгновенным значениям исходного сигнала, взятых в моменты возникновения импульсов переносчика. На этом же рисунке длительности импульсов равны длительностям импуль­сов переносчика, но, в общем случае, как это будет показано далее, могут и отличаться от них.

Для определения спектра АИМ сигнала воспользуемся методом суперпозиции, считая, что процесс модуляции линейный. В этом случае для определения спектра достаточно перемножить одну из спектральных составляющих модулирующего сигнала со спектром переносчика и распространить результат на всю сумму спектраль­ных составляющих сигнала.

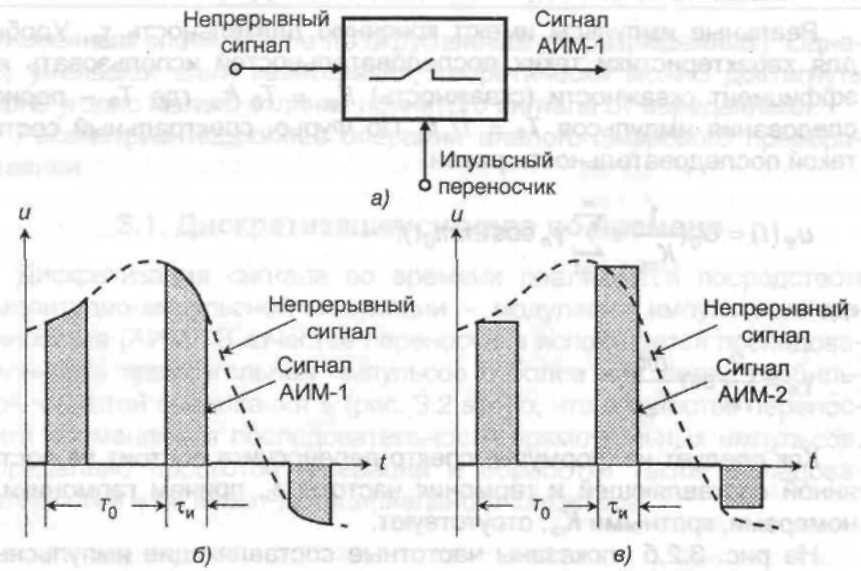
Рис. 3. Виды амплитудно-импульсной модуляции: а - модулятор АИМ-1; б - АИМ-1; в - АИМ-2

Для двуполярного сигнала имеем

где ω_i, = 2nf_i - частота i'-й спектральной составляющей; θ_i - ее на­чальная фаза; m_i, - коэффициент, характеризующий ее амплитуду. Сумма всех коэффициентов т, равна единице, т.е.

причем i-число спектральных составляющих.

Из формулы следует, что спектр канального сигнала (модулиро­ванной импульсной последовательности) будет состоять из спектра исходного сигнала и спектров нижней и верхней боковых полос у каждой составляющей спектра импульсной последовательности, как это показано на рис. 4,а. В ЦСП первых поколений применял­ся однополярный исходный сигнал, поэтому

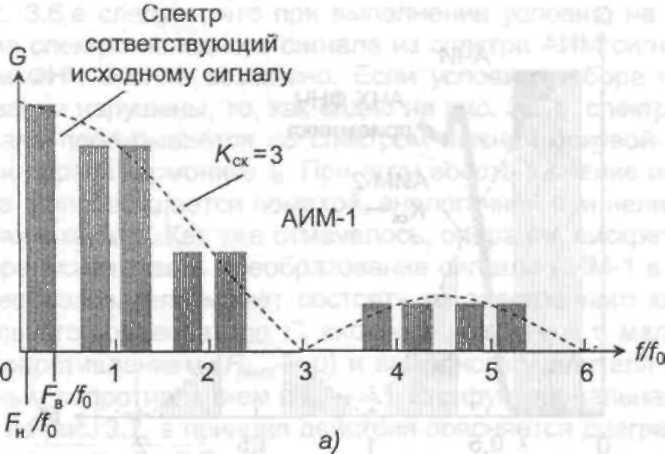
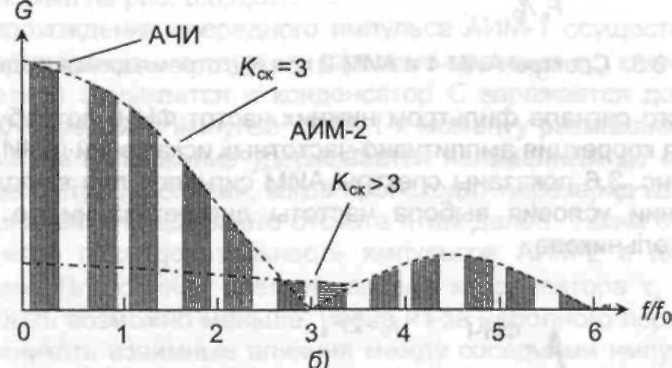
Рис. 4. Спектры сигналов при АИМ-1 (а) и АИМ-2 (б)

и канальный сигнал содержал также, кроме указанных частотных составляющих, все частотные составляющие модулируемой после­довательности. Наличие в канальном сигнале исходного спектра позволяет восстанавливать на приеме исходный сигнал с помощью фильтра нижних частот с частотой среза F_B.

Данный анализ справедлив для АИМ-1. Для АИМ-2 результат несколько отличен. Это видно из рис. 4,б. По мере увеличения скважности импульсов переносчика, это отличие становится все менее заметным. Однако в некоторых видах оборудования ЦТС на приеме используются амплитудно-модулированные импульсы, с шириной, приближающейся к тактовому интервалу, т.е. с К_СК, стре­мящимся к единице. Этот случай иллюстрирует рис. 5. Очевидно, что при восстановлении исходного сигнала (при выделении спектра

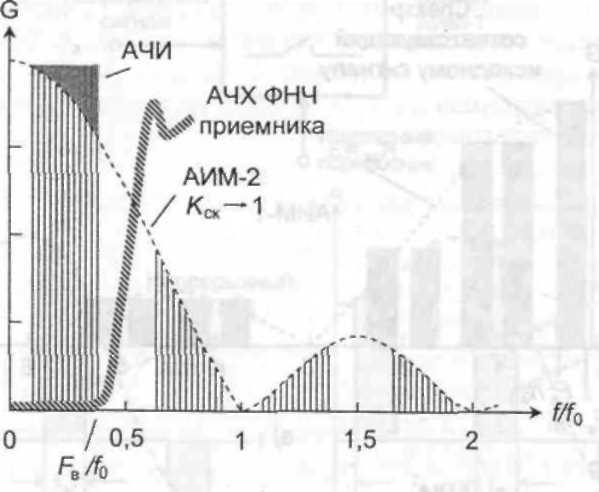
Рис. 5. Спектры АИМ-1 и АИМ-2 при К_ск, стремящимся к единице

исходного сигнала фильтром нижних частот ФНЧ) потребуется не­сложная коррекция амплитудно-частотных искажений (АЧИ).

На рис.6 показаны спектры АИМ сигналов при выполнении и нарушении условия выбора частоты дискретизации по теореме В.А. Котельникова.

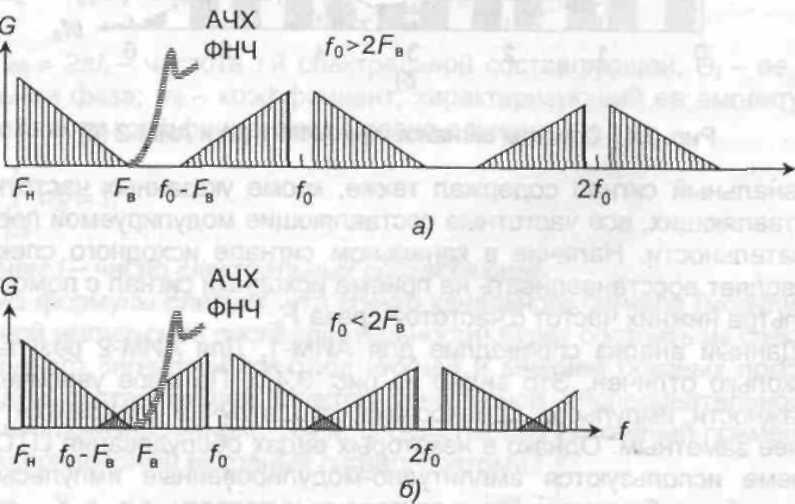
Рис. 6. Спектры АИМ сигнала для случаев выполнения условия (а) и невыполнения условия теоремы Котельникова (б)

Из рис. 6,а следует, что при выполнении условия, на приеме выделение спектра исходного сигнала из спектра АИМ сигнала по­средством ФНЧ вполне возможно. Если условия выбора частоты дискретизации нарушены, то, как видно на рис. 6,б, спектр исход­ного сигнала перекрывается со спектром нижней боковой полосы частот при первой гармонике f₀- При этом восстановление исходно­го сигнала сопровождается помехой, аналогичной при нелинейных искажениях в канале. Как уже отмечалось, операция дискретизации должна предусматривать преобразование сигнала АИМ-1 в АИМ-2. Такой преобразователь может состоять из электронного ключа К, накопительного конденсатора С, входного усилителя с малым вы­ходным сопротивлением (R_вых—► 0) и выходного усилителя с высо­ким входным сопротивлением (R_вх-»∞). Его функциональная схема показана на рис. 7, а принцип действия поясняется диаграммами, приведенными на рис. 8,а,б. При прохождении очередного импульса АИМ-1 осуществляется его стробирование - в течение короткого времени τ_стр ключ К пре­образователя замыкается и конденсатор С заряжается до напря­жения, которое имел импульс АИМ-1 к моменту размыкания клю­ча. Далее это напряжение удерживается неизменным до момента следующего стробирования, когда происходит перезаряд конденса­тора до значения следующего отсчета и так далее. Таким образом, формируется последовательность импульсов АИМ-2 с плоскими вершинами. Постоянная времени заряда конденсатора τ_з = R_ВЫХС должна быть возможно меньше, иначе из-за неполного перезаряда будут возникать взаимные влияния между соседними импульсами. В случае, если сигнал АИМ-1 групповой, эти влияния будут приво­дить к внятным переходным помехам между каналами. Постоянная времени разряда, равная τ_p = R_ВХС, напротив, выбирается достаточ­но большой, чтобы конденсатор не успел заметно разрядиться за период между моментами стробирования. Это условие гарантирует плоскую вершину импульса АИМ-2, что необходимо для нормально­го проведения последующей операции - кодирования.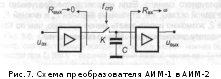

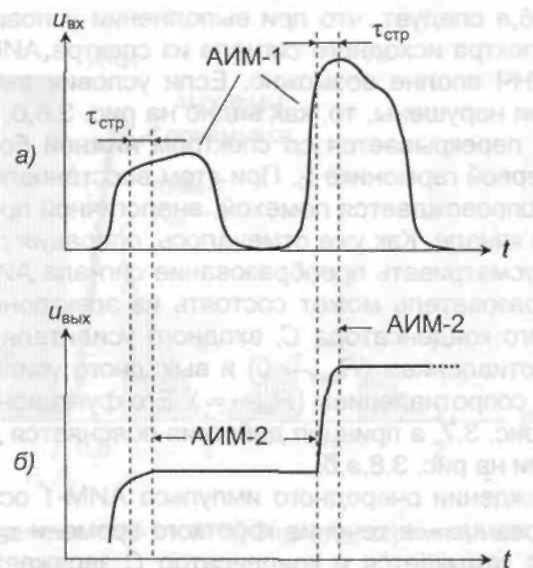
Рис. 8. Диаграммы работы преобразователя АИМ-1 в АИМ-2: а - импульсы АИМ-1 на входе; б - формирование выходного импульса

АИМ-2

Заметим, что частота следования стробирующих импульсов должна совпадать с частотой следования импульсов АИМ-1. Отметим также, что на рис. 7 показана упрощенная схема, реальные же схемы пре­образователей уравновешены относительно общего провода для уменьшения наводок от управляющих цепей на цепи передачи каналь­ных сигналов. Кроме того, электронный ключ должен быть выбран так, чтобы его сопротивление замыкания было бы возможно меньшим (оно увеличивает постоянную времени т₃), а сопротивление размыкания -возможно большим (оно уменьшает постоянную времени т_р).

При выборе частоты дискретизации в соответствии с теоремой В.А. Котельникова учитывается только верхняя частота спектра преобразуемого сигнала. Если же спектр преобразуемого сигнала менее одной октавы, т.е. отношение верхней F_B и нижней F_H частот менее 2, возможно использовать менее высокую, чем по Котельникову, частоту дискретизации'. Можно показать, что

* Спектры, шириной менее октавы, характерны для групповых сигналов те­лекоммуникационных систем с частотным разделением каналов (ТКС ЧРК).

(1)

где f_дк = 2F_B минимальная частота дискретизации по Котельникову, f_ди = 2(F_B - F_H) - минимальная частота дискретизации для случая, если исходный спектр перемещен так, что его нижняя частота рав­на нулю (F_H = 0),

искомая частота дискретизации и n - целое число. При этом, рас­стояние от исходного спектра до ближайших преобразованных со­ставляющих {полоса расфильтровки) будет равно

Число n следует подбирать, начиная с единицы до тех пор, пока не будет выполнено неравенство (1). Поясним сказанное примером.

Пусть исходный сигнал занимает полосу 312...552 кГц (типовая вторичная группа каналов тональной частоты ТКС ЧРК). В соответ­ствии с неравенством (1) определяем: f_ди = 2(552 - 312) = = 480 кГц, f_дK = 552-2 = 1104 кГц, f_д = 2(552+312)/(2-1+1) = 576 кГц (при n > 1 неравенство не выполняется), Δf_p = 576/2 - (552-312) = = 48 кГц. На рис. 9 приведено построение спектров для рассмот­ренного случая. В процессе передачи сигнала происходит смеще­ние принимаемых импульсов со своих тактовых точек (медленные фазовые флуктуации - вандер). Это приводит к появлению ошибки при восстановлении сигнала на приеме.

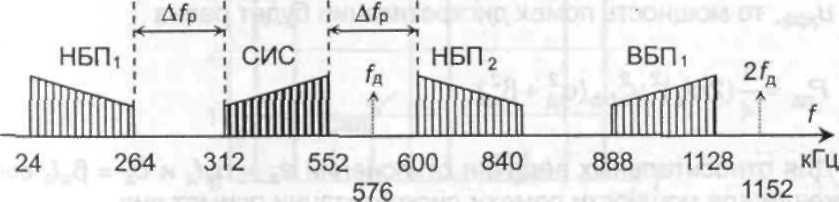
Рис. 9. Спектр дискретизированного группового сигнала: СИС спектр, соответствующий исходному сигналу; НБП1 - нижняя боковая полоса частот при f_д ВБП1 - верхняя боковая полоса частот при f_д; НБП2 -нижняя боковая полоса частот при 2f_д

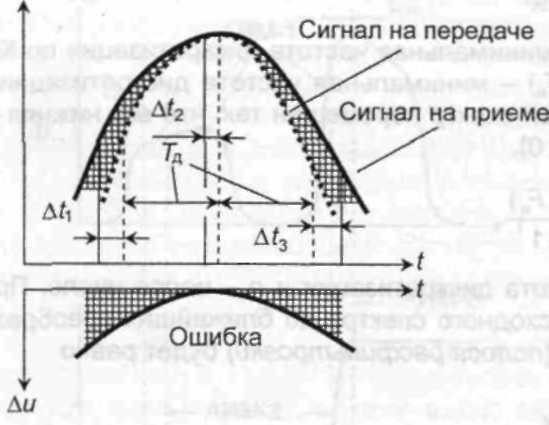
Рис.10. Возникновение ошибки дискретизации

На рис. 10 пунктиром показана форма сигнала на передаче и отмечены тактовые точки, в которых были определены мгновенные значения сигнала.

На приеме (сплошная кривая) форма сигнала изменилась из-за смещения на Δf, моментов восстановления мгновенных значений. Таким образом, восстановленный сигнал может рассматриваться как сумма исходного сигнала и ошибки, которая и определяет величину помехи дискретизации, воспринимаемой как нелинейные искажения в канале. Определим величину этой помехи.

Если абсолютные значения среднеквадратических отклонений импульсов от тактовых точек по причине некорректной работы ге­нераторного оборудования оконечных станций и регенераторов со­ответственно равны, а эффективное значение сигнала рав­но u_эфф, то мощность помех дискретизации будет равна

Для относительных величин отклоненийвыражение для мощности помехи дискретизации примет вид

Защищенность от помех дискретизации может быть подсчитана по формуле

Величина защищенности от помех дискретизации A_зпд в простом (при отсутствии транзитов) основном цифровом канале (ОЦК, ско­рость передачи - 64 кбит/с) не должна быть ниже 34 дБ. В каналах, состоящих из л простых, требуемая защищенность может быть снижена на величину, равную 10lgn

2. Квантование сигнала по уровню

2.1. Равномерное квантование

Квантование сигнала по уровню является главной операцией аналого-цифрового преобразования сигнала и заключается в округ­лении его мгновенных значений до ближайших разрешенных, как это показано на

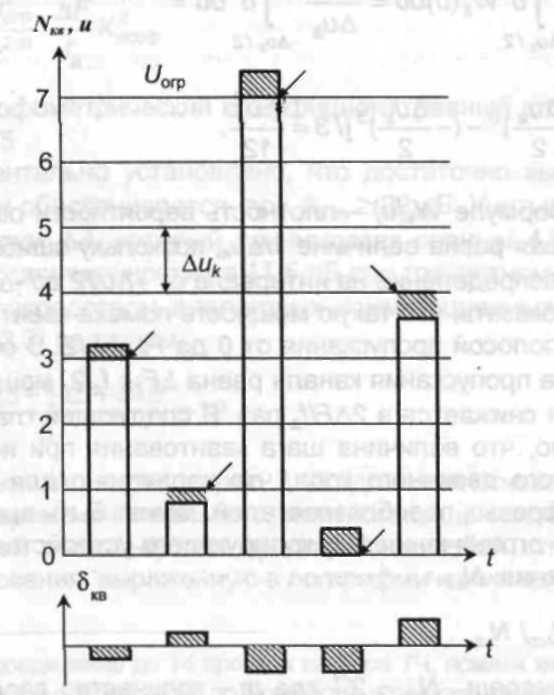
Рис. 11. Возникновение ошибки квантования

На нем показан АИМ сигнал, по вертикали отмечены восемь уровней квантования (с 0-го по 7-й). Расстояния между уровнями одинаковые, т.е. имеет место равномерное или линейное квантова­ние, и равны шагу квантования Δи_к. Стрелками на рисунке отмече­ны значения, до которых округляются амплитуды исходных импуль­сов. Напряжение 7-го уровня соответствует напряжению ограниче­ния U_огр, амплитуда 4-го импульса равна нулю. Очевидно, при кван­товании сигнала возникают ошибки δ_кв (затемненные поля на рисунке), величина которых случайна, имеет равномерное распре­деление и не превышает значения Δи_к / 2. Таким образом, сигнал после квантования представляет собой сумму исходного сигнала и сигнала ошибки (показанные на нижнем графике рис. 11), который воспринимается как флуктуационный шум.

Мощность помехи квантования может быть найдена следующим образом

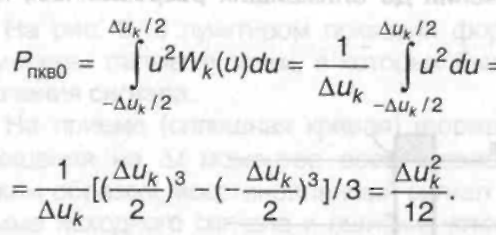
В этой формуле W_k(u) - плотность вероятности ошибки кванто­вания, которая равна величине 1/Δи_к , поскольку ошибка имеет рав­номерное распределение на интервале от

Можно показать, что такую мощность помеха квантования имеет в канале с полосой пропускания от 0 до F_B = f_д/2. В общем случае, когда полоса пропускания канала равна ΔF < f_Д/2, мощность помехи квантования снижается в 2ΔF/f_Д раз. В следующей главе (§ 3.3) бу­дет показано, что величина шага квантования при использовании симметричного двоичного кода, что характерно для современных аналого-цифровых преобразователей, может быть выражена через напряжение ограничения Uогр кодирующего устройства и число ша­гов квантования N_KB

В свою очередь, где т - количество двоичного разрядов кода. С учетом сказанного выражение для мощности помех квантования в канале может быть записано в следующем виде

(2)

Мощность помехи квантования следует сравнить с минималь­ным значением квантуемого сигнала, откуда можно будет опреде­лить

необходимое число шагов квантования и, следовательно, чис­ло разрядов двоичного кода т.

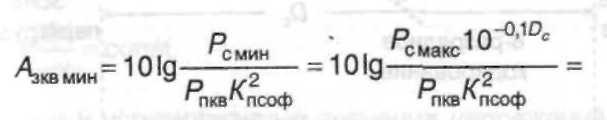
(3)

Воспользовавшись формулами (2) и (2.3) несложно опреде­лить защищенность от шумов квантования для наиболее слабых сигналов:

где К_псоф - псофометрический коэффициент, равный для канала ТЧ величине 0,75

Экспериментально установлено, что достаточно высокое каче­ство передачи обеспечивается при Аз кв ≥ 22 дБ. Учитывая эксплуа­тационный запас ΔА который принимается равным 4,5 дБ, и сни­жение помехозащищенности на 11,5 дБ при транзитном соединении каналов ТЧ посредством аналоговых коммутационных устройств', из формулы (3) получаем:

При этом, как это видно из рис. 12, для всех мгновенных значе­ний сигнала, кроме минимального, помехозащищенность оказывает­ся завышенной поскольку она представляет собой относительную ошибку квантования, выраженную в логарифмических единицах, т.е.

Допускается соединение до 14 простых каналов ТЧ, помехи квантования со­единенных каналов суммируются по мощности, и поэтому снижение защищен­ности может достигать значения 10lg14 = 11,5 дБ, откуда минимально допус­тимая защищенность оказывается равной А з кв мин = 22 + 4,5 + 11,5 = 38 дБ.

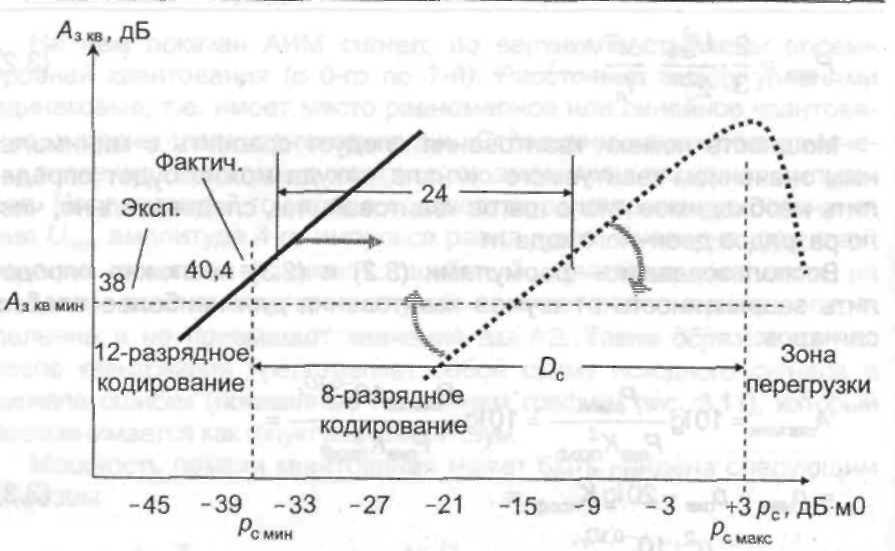
Рис. 12. Защищенность от шумов квантования при равномерном квантовании

Помехозащищенность пропорционально растет с ростом уровня сигнала до тех пор, пока не будет достигнут р_{с макс}, соответствую­щий напряжению ограничения. Дальнейший рост сигнала приведет к появлению ошибки из-за ограничения сигнала по амплитуде и по­мехозащищенность начнет снижаться за счет помех ограничения (перегрузки), как это показано на рис. 12 для характеристики с 8-разрядным кодированием. Начало спада характеристики защи­щенности из-за помех ограничения зависит от параметров сигнала и прежде всего от его пикфактора. Чем выше пикфактор сигнала, тем раньше, по мере его роста, в отдельные моменты будет проис­ходить ограничение его амплитуды и, следовательно, раньше нач­нется спад характеристики помехозащищенности.

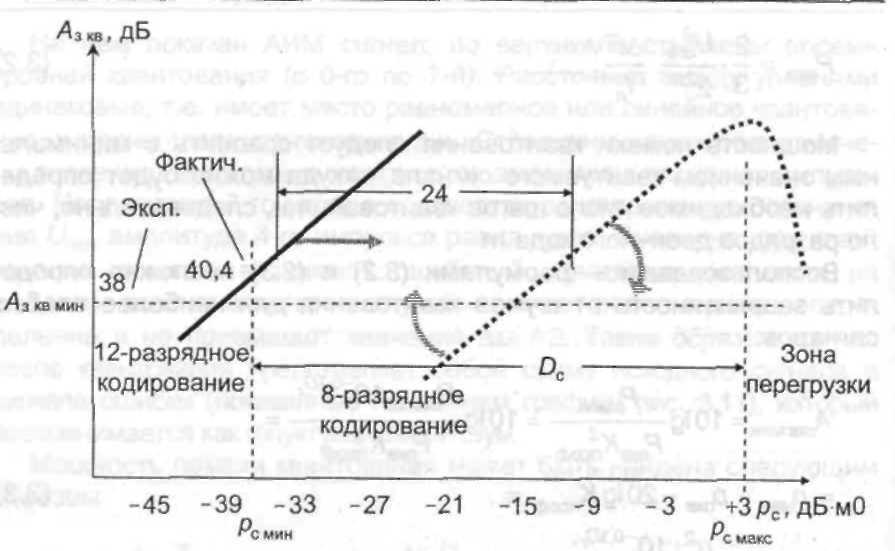
Рис. 12. Защищенность от шумов квантования при равномерном квантовании