Постановка задачи.

Среди совокупности n неделимых предметов, каждый j-й (j=1, 2, … , n) из которых обладает по i-й характеристике показателем a_ij и полезностью c_î, найти такой набор, который позволяет максимизировать эффективность использования ресурсов величины b_i (i=1, 2, … , m).

Математическая модель этой задачи может быть представлена следующим образом: в области, определенной условиями

найти решение x=(x₁, x₂, …, x_n), при котором максимизируется (минимизируется) значение целевой функции

(7)

Если n₁=n, то (4—7) является моделью задачи целочисленного программирования, если n₁<n — моделью задачи частично целочисленного программирования.

Частным случаем задачи целочисленного программирования является задача с булевыми переменными. Ее математическая модель в общем виде записывается следующим образом: в области, определенной условиями

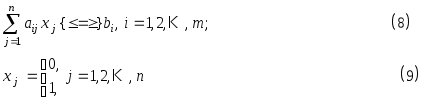
найти решение x=(x₁, x₂, …, x_n), при котором максимизируется (минимизируется) значение функции

(10)

К классу задач целочисленного програмирования примыкают задачи, в которых условие целочисленности всех или части переменных заменено требованием дискретности. А именно, для каждой j-й переменной x_j (j=1, 2,… ,n) заранее определен набор значений (не обязательно целых), которые она может принимать:

Предполагается, что A_jlj , j=1, 2, …, n; l_j=1, 2, … , k_j , проранжированы, т. е. A_j1< A_j2 <…< A_jkj.

Математическая модель общей задачи линейного программирования может быть представлена следующим образом: в области, определенной условиями

найти решение x=(x₁, x₂,…, x_n), при котором максимизируется (минимизируется) линейная функция

(13)

Условие (12) определило название этого класса задач. Если n₁=n, то (11— 13) называется задачей дискретного программирования; если n₁<n, то (11—13) называется задачей частично дискретного программирования.

П р и м е р. В области, опре-деленной условиями

2x₁ +11x₂  38,

x₁ + x₂  7,

4x₁– 5x₂  5,

x₁0, x₂0, x₁, x₂ — целые

найти максимум функции

Z(x₁, x₂)=x₁+x₂.

Р е ш е н и е. Решим задачу геометрически. Область поиска экстремума — многоугольник ODABC, но так как линия уровня целевой функции параллельна стороне АВ многоугольника, экстремум достигается в вершинах А(8/3, 13/3) и В(23/9, 40/9), а также в любой точке отрезка АВ, и равен 7. Однако нас интересуют точки с целочислеными координатами, следовательно, ни А, ни В не являются допустимым решением задачи. Округляя значения координат А, получим А’ (2, 4). Но точка А’ не принадлежит области поиска. Целочисленный оптимум достигается в точках N(3, 2) и M(2, 3) и равен 5. Обе точки внутри области поиска.

Построенный пример показал, что для решения задач с требованием целочисленности необходимо рассмотреть особые методы оптимизации; и, кроме того, оптимальное решенте задач целочисленного программирования не обязательно принадлежит границе многогранника условий, что было характерно для задач линейного программирования.

Методы отсечения.

Запишем общую задачу целочисленного программирования:

в области, определенной условиями

максимизировать функцию

(17)

Назовем задачу (14—17) (G^ц, Z)-задачей. Соответствующую ей задачу без требования целочисленности переменных, т. е. задачу (14, 15, 17) назовем (G, Z)-задачей. Возникает вопрос: нельзя ли решение (G^ц, Z)-задачи получить путем решения некоторой специальным образом построенной задачи без требования целочисленности переменных и такой, что оптимальные решения исходной (G^ц, Z)-задачи и задачи без требования целочисленности переменных будут совпадать. Другими словами: нельзя ли хорошо изученный аппарат решения задач линейного программирования приспособить к решению целочисленных задач. Принципиальный ответ на этот вопрос дает следующая теорема.

Т е о р е м а 1. Пусть G — многогранник, G^ц — множество его целых точек, R — выпуклая линейная оболочка множества G^ц, тогда:

1.  R= R^ц — целочисленный многогранник;

2.  R^ц= G^ц;

3.  R^* — множество опорных решений задачи (G^ц, Z) содержится в многограннике R^ц.

Следствием этой теоремы является тот вывод, что оптимальоне решение задачи, областью определения которой является выпуклая оболочка, натянутая на область поиска целочисленного решения, совпадает с оптимальным решением исходной целочисленной задачи.

Теорема и следствие из нее показывают принципиальную возможность замены решения задачи типа (G^ц, Z) некоторой процедурой построения и решения вспомогательной задачи типа (G, Z), однако не дают алгоритма решений. К тому же построение выпуклой оболочки множества G^ц реальных задач — чрезвычайно сложная, а подчас практически неразрешимая задача.