Графический метод решения задачи линейного программирования.

Графический метод основан на геометрической интерпретации задачи линекйного программирования и применяется в основном при решении задач двумерного пространства. Пусть задача линейного программирования задана в двумерном пространстве, т. е. ограничениясодержат две переменные.

Найти минимальное значение функции

Z=C₁x₁+ C₂x₂ (2.55)

при условиях

(2.56)

õ₁0, õ₂0. (2.57)

Допустим, что система (2.56) при условии (2.57) совместна и ее многоугольник решений ограничен. Каждое из неравенств (2.56) и (2.57) определяет полуплоскость с граничной прямой a_i1x₁+a_i2x₂=b (i=1, 2, ..., m), x₁=0, x₂=0. Линейная функция (2.55) при фиксированных значениях Z является уравнением прямой линии C₁х₁+ C₂x₂=const. Построим многоугольник решений системы ограничений (2.56) и график линейной функции (2.55) при Z = 0 (рис.2.6). Тогда поставленной задаче линейного программирования можно дать следующую интерпретацию. Найти точку многоугольника решений, в которой прямая C₁х ₁+ C₂x₂=const — опорная и функция Z при этом достигает минимума.

Значения Z=C₁х₁+C₂x₂ возрастают в направлении вектора N=(C₁,C₂), поэтому прямую Z=0 передвигаем параллельно самой себе в направлении вектора N.

Из рис.2.6 следует, что прямая дважды становится опорной по отношению к многоугольнику решений (в точках A и C, причем минимальное значение принимает в точке А. Координаты точки А (х₁; х₂) находим, решая систему уравнений прямых АВ и АЕ.

При нахождении решения задачи (2.55)—(2.57) могут встретиться случаи, изображенные на рис. 2.7—2.10. Рис. 2.7 характеризует случай, когда целевая функция принимаетминимальное значение в единственной точке А. Из рис. 2.8 видно, что минимальное значение целевая функция принимает в любой точке отрезка АВ. На рис. 2.9 изображен случай, когда целевая функция не ограничена снизу на множестве допустимых решений, а на рис. 2.10 — случай, когда система ограничений задачи несовместна.

рис.2.7

рис.2.8

рис.2.9

рис.2.10

Отметим, что нахождение максимального значения отличается от нахождения минимального значения при тех же ограничениях лишьтем, что линия C₁х₁+C₂x₂=const передвигается не в направлении вектора N, а в противоположном направлении.

Итак, нахождение решения задачи линейного программирования (2.55)—(2.57) на основе ее геометрической интерпретации включает следующие этапы:

1. Строят прямые, уравнения которых получаются в результате замены в ограничениях (2.56) и (2.57) знаков неравенств на знаки точных равенств.

2. Находят полуплоскости, определяемые каждым из ограничений задачи.

3. Находят многоугольник решений.

4. Строят вектор N(C₁;C₂),

5. Строят прямую C₁х₁+ C₂x₂=const.

6. Передвигают эту прямую в направлении вектора N, в результате чего либо находят точку (точки), в которой целевая функция принимает минимальное значение, либо устанавливают неограниченность снизу функции на множестве планов.

7. Определяют координаты точки минимума функции на множестве планов.

П р и м е р 1. Задача использования сырья. Найти максимальное значение функции Z=50x₁+40x₂ при условиях

Р е ш е н и е. Построим многоугольник решений (рис.2.11). Для этого в системе x₁Ox₂ на плоскости изобразим граничные прямые

2x₁+5x₂=20,

8x₁+5x₂=40,

5x₁+6x₂=30,

x₁=0, x₂=0.

Взяв какую-нибудь точку, например, начало координат, установим, какую полуплоскость определяет оответствующее неравенство. Многоугольником решений данной задачи является ограниченный пятиугольник OABCD.

Для построения прямой 50x₁+40x₂=0 строим радиус-вектор N=(50; 40)=10(5; 4) и через точку О проводим прямую, перпендикулярную ему. Построенную прямую Z=0 перемещаем параллельно самой себе в направлении вектора N. Из рисунка следует, что опорный план по отношению к многоугольнику решений эта прямая становится в точке C, где функция Z принимает максимальное значение. Точка C лежит на пересечении прямых 8x₁+5x₂=40 и 5x₁+6x₂=30. Для определения ее координат решим систему уравнений

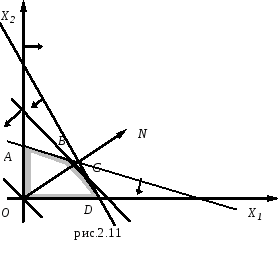
Оптимальный план задачи: х₁=90/233.9, х₂=40/231.7. Подставляя значения х₁ и х₂ в линейную функцию, получаем Z_max=503.9+401.7260.3.

Таким образом, для того чтобы получить максимальную прибыль в размере 260.3 руб., необходимо запланировать производство 3.9. ед. продукции А1 и 1.7 ед. продукции А2.