3. Поле бесконечной заряженной нити

Рассмотрим поле, создаваемое бесконечной нитью равномерно заряженной с линейной плотностью

Из соображений симметрии следует, что линии напряженности имеют вид радиальных прямых, перпендикулярных к нити, а величина напряженности может зависеть только от расстояния r от нити.

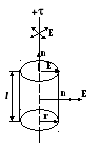В качестве замкнутой поверхности выберем в данном случае цилиндр коаксиальный с нитью. Пусть r – радиус этого цилиндра, а l – его длина. Для вычисления потока вектора опять разобъем замкнутую поверхность на две части – боковую и площадь оснований.

l

Для боковой поверхности и, следовательно, Еn=E.

Для оснований и, следовательно Еn=0. На боковой поверхности Е имеет постоянную величину и, следовательно, ее можно вынести за знак интеграла.

Внутрь цилиндра попадает заряд .

Применяя теорему Гаусса получаем

Поле заряженной сферической поверхности

Рассмотрим сферу радиуса R, равномерно заряженную по поверхности с поверхностной плотностью заряда.

Вследствие равномерного распределения заряда по поверхности сферы, поле, создаваемое этим зарядом должно обладать сферической симметрией. Это означает, что линии вектора Е должны быть направлены по радиусам, проведенным из центра сферы, а численное значение Е может зависеть только от расстояния r до центра сферы.

Рассмотрим сферическую поверхность радиуса r. Пусть r>R. Поток через эту поверхность

.

Еn=E, т.к. и величина Е постоянна на всей поверхности сферы радиуса r. Внутрь этой поверхности попадает весь заряд, находящийся на сфере радиуса R.

По теореме Гаусса:

.

Если мы рассмотрим сферическую поверхность радиуса r<<R, то внутри такой сферы зарядов не будет и, следовательно, Е внутри сферы равно нулю.

Таким образом, внутри сферической поверхности, заряженной с постоянной поверхностной плотностью , поле отсутствует. Вне этой поверхности поле имеет такой же вид, как поле точечного заряда той же величины, помещенного в центре сферы. Можно записать формулу несколько иначе:

На поверхности сферы r=R: .

Поле объемно заряженной сферы

Рассмотрим сферу радиуса R, заряженную с постоянной объемной плотностью . Поле такой сферы обладает центральной симметрией. Для поля вне сферы (r>R) очевидно будет такой же результат, что и для сферы заряженной по поверхности, т.е.

Для точек внутри сферы результат будет другим. Если мы рассмотрим сферу радиуса r<R, то заряд внутри такой сферы будет равен

Применяя теорему Гаусса получим:

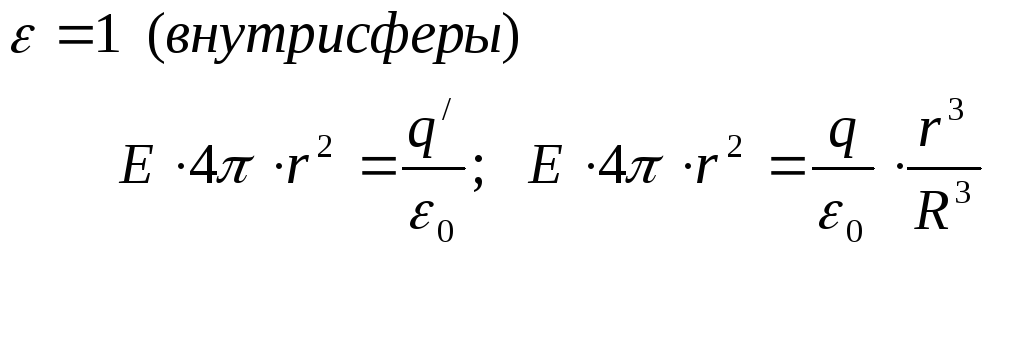
Таким образом, если внутри сферы ε=1, а вне ε≠1, то для напряженности поля имеем:

(r≤R) – внутри сферы

- вне сферы

Для случая когда и вне сферы ε=1, график зависимости E(r) имеет вид показанный на рисунке – внутри сферы Е линейно растет, достигает максимального значения на поверхности и затем убывает обратно пропорционально r², как для точечного заряда.