6. Магнитное поле соленоида.

Соленоид представляет собой провод, плотно навитый на цилиндрический каркас. Линии напряженности магнитного поля соленоида имеют вид:

В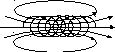нутри густо, вне соленоида - редко.

Если длина соленоида во много раз больше диаметра его витков (l>>d), соленоид можно считать бесконечно длинным. Магнитное поле такого соленоида целиком сосредоточено внутри него. Вне соленоида H=0.

Получим выражение для напряженности магнитного поля соленоида, используя формулу для циркуляции вектора Н.

Возьмем прямоугольный контур 1-2-3-4. Циркуляцию вектора по этому контуру можно написать в виде:

Второй и четвертый интегралы равны нулю, так как на этих участках H перпендикулярны вектору dl и следовательно.

Третий интеграл равен нулю, поскольку H=0 вне соленоида. Следовательно, остается только первый интеграл На участке 1-2 H параллельно dl, и постоянно для всех точек отрезка .

(1)

Согласно формуле о циркуляции вектора H имеем:

(2)

Здесь I_k- ток, охватываемый одним витком соленоида. Если обозначить через N общее число витков соленоида, охватываемых контуром 1-2-3-, то

где I-сила тока в соленоиде.

Тогда

(3)

Сравнивая формулы (1) и (3) получим формулу для напряженности магнитного поля соленоида

(4)

Здесь n=N/l – число витков, приходящихся на единицу длины соленоида.

Полученный результат не зависит от того, на каком расстоянии от оси (но внутри соленоида) располагается отрезок 1-2. Таким образом, всюду внутри соленоида H одинаково и имеет величину, определяемую формулой (4), т.е. магнитное поле внутри соленоида однородное (конденсатор - однородное электростатическое поле и сосредоточено полностью внутри конденсатора).

Если мысленно разделить бесконечный соленоид некоторой плоскостью перпендикулярной оси соленоида, то магнитное поле в точках этой плоскости будет создаваться в одинаковой мере обеими половинками соленоида. Если теперь убрать половину соленоида, то у конца полубесконечного соленоида H будет равно:

(5)

Практически, если длина соленоида значительно больше его диаметра, то формула (4) справедлива для средней части соленоида, а формула (5) для точек вблизи концов. Таким образом, магнитное поле уменьшается к краю. Подобный краевой эффект отсутствует у соленоида, свитого в кольцо, так называемого тороида. Все магнитное поле сосредоточено внутри тороида. Линии вектора H представляют собой замкнутые концентрические окружности. Выбирая одну из таких окружностей за контур обхода, и применяя теорему о циркуляции, легко доказать, что при условии R>>r получается такая же формула, что и для бесконечно длинного соленоида.

В этом случае поле однородно в каждом из сечений тороида. Но в разных сечениях H направлено различно, и имеет смысл говорить об однородности поля в пределах всего тороида только условно, имея в виду только модуль вектора .

7. Сила, действующая на проводник с током в магнитном поле (закон Ампера).

Мы видели , что для обнаружения и исследования магнитного поля применяется контур с током. На этот контур действует в магнитном поле вращающий момент, что является очевидным следствием того, что на отдельные элементы контура действуют механические силы. Существование таких сил можно обнаружить на следующем опыте.

П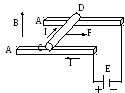о металлическим горизонтальным шинам A может перемещаться стержень CD. К шинам подключен источник тока Е, вследствие чего по проводнику протекает ток I. Имеется однородное магнитное поле В направленное вверх. При прохождении через стержень электрического тока стержень покатится. Это свидетельствует о том, что на стержень действует механическая сила. Величину этой силы легко измерить, уравновесив её каким-либо механическим образом. Опыт показывает, что эта сила может быть выражена формулой:

,

где I – ток, текущий по проводнику, l – длина проводника, В – индукция магнитного поля, k₂ – коэффициент пропорциональности, зависящий от системы единиц. В СИ k₂=1.

Направлена эта сила перпендикулярно плоскости, содержащей и .

Опыт показывает, что, если поле параллельно I, то сила равна нулю. Это означает, что сила F обусловлена лишь той составляющей поля В, которая перпендикулярна I, т.е. составляющей B_n.

Таким образом, если направлено под углом к I, то

(1).

где  - угол между направлениями B и I.

Формула (1) выражает закон Ампера.

Закон Ампера легко обобщить на случай неоднородного магнитного поля и проводника произвольной формы. В самом деле, бесконечно малый элемент dl проводника любой формы можно считать прямолинейным, а магнитное поле в области, занятой элементом dl можно считать однородным.

Поэтому в общем случае закон Ампера имеет вид:

(2)

Закон Ампера, записанный в форме (2) не указывает направления силы dF и поэтому не определяет её полностью. Как показали опыты, направление силы dF можно определить по правилу левой руки: В – в ладонь, 4 пальца – I, большой палец – dF. Это правило очень удобно, но лишь когда элемент dll проводника с током перпендикулярен к направлению магнитного поля. Поэтому лучше пользоваться более универсальным правилом – правилом буравчика: вращать ручку от I к В в направлении угла меньшего , тогда поступательное движение буравчика укажет направление силы. Иными словами вектор dF совпадает по направлению с векторным произведением [dl , B]. Поэтому закон Ампера можно записать в векторной форме.

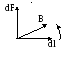
(CИ)