
- •1. Магнитное поле. Индукция и напряженность магнитного поля
- •2. Закон Био-Савара-Лапласа
- •3. Напряженность магнитного поля прямолинейного проводника с током
- •4. Напряженность магнитного поля кругового тока
- •5. Циркуляция вектора .
- •6. Магнитное поле соленоида.
- •7. Сила, действующая на проводник с током в магнитном поле (закон Ампера).
- •8. Взаимодействие параллельных токов.
- •9. Сила, действующая на заряд, движущийся в магнитном поле (Сила Лоренца).
- •10. Движение заряженных частиц в однородном магнитном поле.
- •11.Ускорители заряженных частиц (циклотрон).
- •12. Экспериментальное определение удельного заряда частиц. Масс- спектрограф.
- •13. Эффект Холла.
- •14. Магнитный поток
- •15. Работа, совершаемая при перемещении проводника с током в магнитном поле
- •16. Явление электромагнитной индукции. Закон Фарадея.
- •17. Вывод закона Фарадея.
- •18. Самоиндукция. Индуктивность.
- •19. Взаимная индукция.
- •20. Вихревые токи (токи Фуко). Скин-эффект.
- •21. Энергия магнитного поля.
- •22. Ток смещения.
- •23. Уравнения Максвелла.
- •24. Магнитные моменты электронов и атомов.
- •25. Атом в магнитном поле.
- •26. Макроскопическое описание магнитного поля в веществе
- •27. Диамагнетики и парамагнетики
- •28. Ферромагнетики
4. Напряженность магнитного поля кругового тока
Р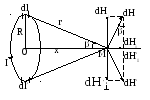 ассмотрим
поле, создаваемое током, текущим по
тонкому проводнику, имеющему форму
окружности радиусом
ассмотрим
поле, создаваемое током, текущим по
тонкому проводнику, имеющему форму
окружности радиусом
![]() (круговой ток). Найдем напряженность
на оси кругового тока на расстоянии
(круговой ток). Найдем напряженность
на оси кругового тока на расстоянии
![]() от плоскости, в которой лежит контур.
По закону Био- Савара-Лапласа
напряженность создаваемая элементом
проводника dl равна
от плоскости, в которой лежит контур.
По закону Био- Савара-Лапласа
напряженность создаваемая элементом
проводника dl равна
![]()
![]() ,
=90o
следовательно,
,
=90o
следовательно,
![]() .
.
Вектор
![]() составляет некоторый угол с осью ОМ.
Каждому элементу
составляет некоторый угол с осью ОМ.
Каждому элементу
![]() можно
сопоставить диаметрально противоположный
элемент dl
Для этих элементов перпендикулярные
составляющие
dH
и
можно
сопоставить диаметрально противоположный
элемент dl
Для этих элементов перпендикулярные
составляющие
dH
и
![]() взаимно
уничтожаются, а параллельные
dHll
и dHll
составляющие складываются. Следовательно,
результирующее поле будет направлено
по оси ОМ. Зная направление, мы сможем
теперь определить величину
взаимно
уничтожаются, а параллельные
dHll
и dHll
составляющие складываются. Следовательно,
результирующее поле будет направлено
по оси ОМ. Зная направление, мы сможем
теперь определить величину
![]() ,
сложив составляющие dHll
всех элементов
контура.
,
сложив составляющие dHll
всех элементов
контура.
![]()
![]()
![]()
Но
![]() ,
тогда
,
тогда
![]() - напряженность магнитного поля на
оси кругового тока
- напряженность магнитного поля на
оси кругового тока
Положив
![]() =0,
получим формулу для напряженности поля
в центре кругового витка:
=0,
получим формулу для напряженности поля
в центре кругового витка:
![]()
5. Циркуляция вектора .
В электростатике мы ввели понятие циркуляции вектора напряженности как величину равную:
![]()
![]() -
проекция E
на направление касательной к контуру
L.
-
проекция E
на направление касательной к контуру
L.
Было показано, что циркуляция вектора Е равна нулю. Физический смысл циркуляции вектора Е - работа по перемещению единичного заряда (F=E при q=1, Edl=A при q=1) по замкнутому контуру. Но в механике было показано, что поле, в котором работа по замкнутому контуру равна нулю, называется потенциальным. Таким образом равенство нулю циркуляции вектора Е говорит о том, что электростатическое поле является потенциальным.
Рассмотрим
теперь, чему равна циркуляция вектора
индукции магнитного поля. Возьмем контур
L, охватывающий
прямой ток и вычислим для него циркуляцию
вектора
![]() :
:
![]()
Р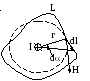 ассмотрим
случай, когда контур лежит в плоскости
перпендикулярной к току. Пусть ток
перпендикулярен к плоскости чертежа и
направлен за чертеж. Линии напряженности
представляют собой окружности, а вектор
ассмотрим
случай, когда контур лежит в плоскости
перпендикулярной к току. Пусть ток
перпендикулярен к плоскости чертежа и
направлен за чертеж. Линии напряженности
представляют собой окружности, а вектор
![]() направлен по касательной к окружности.
направлен по касательной к окружности.
![]()
![]() -проекция
вектора
-проекция
вектора
![]() на направление
на направление
![]() .
.
Но
![]() можно представить в виде:
можно представить в виде:
![]() =
=
![]() ,
где
,
где
![]() -расстояние
от прямого тока до
-расстояние
от прямого тока до
![]() ,
,
![]() -
угол, под которым виден элемент
-
угол, под которым виден элемент
![]() контура
L
из центра
окружности.
контура
L
из центра
окружности.
![]()
![]()
Интегрируя
вдоль всего замкнутого контура
L и учитывая,
что при этом угол
![]() изменяется от нуля до
изменяется от нуля до
![]() ,
получим:
,
получим:
![]()
Таким
образом,
циркуляция вектора
![]() магнитного поля прямолинейного бесконечно
длинного проводника с током
магнитного поля прямолинейного бесконечно
длинного проводника с током
![]() вдоль замкнутого контура, охватывающего
проводник численно равна
вдоль замкнутого контура, охватывающего
проводник численно равна
![]() .
.
Если контур не охватывает проводник с током, то:
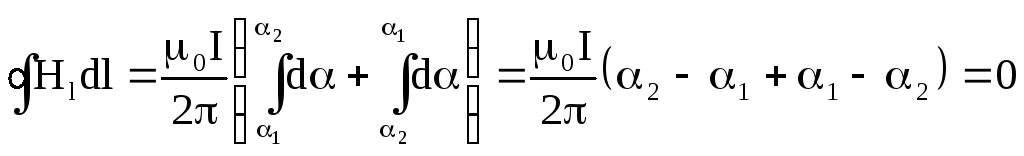

Таким
образом,
если контур тока не охватывает, циркуляция
вектора
![]() равна нулю.
равна нулю.
Мы
рассмотрели циркуляцию вектора
![]() для случая прямого тока. Но можно доказать
что для проводников любой формы и
размеров циркуляция вектора индукции
магнитного поля вдоль любого замкнутого
контура равна силе тока в проводнике,
охватываемом этим контуром.
для случая прямого тока. Но можно доказать
что для проводников любой формы и
размеров циркуляция вектора индукции
магнитного поля вдоль любого замкнутого
контура равна силе тока в проводнике,
охватываемом этим контуром.
Если
контур охватывает несколько токов,
циркуляция
![]() равна их алгебраической сумме.
равна их алгебраической сумме.
![]() (*)
(*)
Вычисляя сумму токов, положительным нужно считать такой ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления будет отрицательным.
В электротехнике уравнение (*) называется законом полного тока для токов проводимости.
Из
сопоставления выражений для циркуляции
вектора Е электростатического поля и
вектора
![]() магнитного поля следует, что между этими
полями имеется принципиальное различие.
Циркуляция вектора Е равна нулю и
электростатическое поле является
потенциальным. Циркуляция вектора
магнитного поля следует, что между этими
полями имеется принципиальное различие.
Циркуляция вектора Е равна нулю и
электростатическое поле является
потенциальным. Циркуляция вектора
![]() отлична от нуля, если контур по которому
берется циркуляция, охватывает ток.
Поля, обладающие таким свойством,
называют вихревыми (соленоидальными).
Магнитному полю нельзя приписать
потенциал, который был бы связан с
отлична от нуля, если контур по которому
берется циркуляция, охватывает ток.
Поля, обладающие таким свойством,
называют вихревыми (соленоидальными).
Магнитному полю нельзя приписать
потенциал, который был бы связан с
![]() так
же как
так
же как
![]() с Е (Е=-grad
с Е (Е=-grad![]() ).Кроме
того линии напряженности электростатического
поля начинаются и заканчиваются на
зарядах. Линии магнитной индукции всегда
замкнуты, что указывает на отсутствие
в природе магнитных зарядов.
).Кроме
того линии напряженности электростатического
поля начинаются и заканчиваются на
зарядах. Линии магнитной индукции всегда
замкнуты, что указывает на отсутствие
в природе магнитных зарядов.
Закон полного тока имеет для расчета магнитных полей постоянного электрического поля такое же важное значение, как и теорема Гаусса для расчета электростатических полей. В качестве примера рассмотрим применение закона полного тока к расчету магнитного поля соленоида.
