2. Закон Био-Савара-Лапласа

После опытов Эрстеда началось интенсивное изучение магнитного поля постоянного электрического тока. В 1820 году французские ученые Био и Савар исследовали магнитные поля, создаваемые в воздухе прямолинейным током, круговым током, катушкой с током и т. д. На основании многочисленных опытов они пришли к следующим выводам:

1. во всех случаях напряженность магнитного поля зависит прямо пропорционально от силы тока ;

2. напряженность зависит от формы и размеров проводника;

3. напряженность в произвольной точке поля зависит от расположения этой точки по отношению к проводнику с током.

Лаплас проанализировал экспериментальные данные, полученные Био и Саваром. Лаплас учел векторный характер напряженности магнитного поля и высказал гипотезу о том, что магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока.

Для напряженности магнитного поля создаваемого элементом тока длины , Лаплас получил формулу:

, ,

эта формула и выражает закон Био-Савара-Лапласа, где коэффициент пропорциональности, зависящий от системы единиц; - сила тока; - вектор, совпадающий с направлением тока и численно равный длине элемента проводника; - вектор, проведенный от элемента тока в ту точку, в которой определяется , модуль этого вектора.

Направлен вектор перпендикулярно к плоскости, проходящей через и точку, в которой вычисляется поле, причем так, что вектора ,

, связаны правилом правого винта (буравчика).

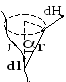В СИ: . Тогда

.

В соответствии с принципом суперпозиции напряженность магнитного поля проводника с током конечных размеров и произвольной формы равна векторной сумме напряженностей элементарных магнитных полей, создаваемых всеми отдельными участками этого проводника

; если, , , тогда .

3. Напряженность магнитного поля прямолинейного проводника с током

Рассмотрим прямолинейный проводник с током АВ конечной длины. Найдем напряженность магнитного поля создаваемого этим проводником в точке М. Для этого нужно весь проводник разбить на элементарные отрезки и для каждого из них вычислить по формуле Био-Савара-Лапласа -

;

Вектора и для всех участков проводника лежат в плоскости чертежа. Поэтому все вектора имеют в точке М одинаковое направление (на нас). Поэтому сложение векторов можно заменить сложением их модулей, т. е. проинтегрировать:

Чтобы произвести интегрирование, выразим и через одну независимую переменную . Тогда

,.

Подставляя и в исходный интеграл, получим:

,

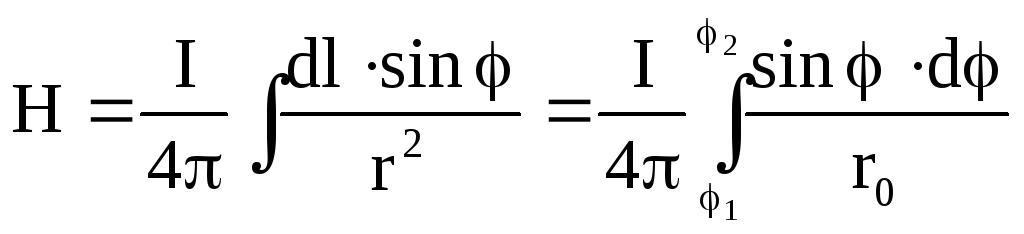где ₁ и ₂ - значения угла для крайних точек проводника АВ.

.

Если проводник бесконечно длинный, то и тогда формула будет выглядеть так:

Это выражение пригодно и для конечного проводника, если , где L – длина проводника, d – диаметр проводника.

Также как для электрического поля распределение магнитного поля в пространстве можно изображать графически с помощью линий напряженности.

Линии напряженности магнитного поля прямого тока представляют собой систему охватывающих проводник концентрических окружностей. Т. к. , то, чем ближе к току, тем гуще расположены линии напряженности. Вектор направлен по касательной и определяется по правилу буравчика.