21. Энергия магнитного поля.

Рассмотрим замкнутую цепь.

З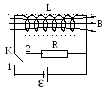амкнем соленоид L на батарею, в нем установится ток I и в соленоиде возникнет магнитное поле. Переключим ключ в положение 2. Через сопротивление R потечет ток самоиндукции. Работа, совершенная этим током за время dt:

Работа, совершаемая за все время, в течение которого происходило убывание тока (и магнитного поля) будет равна:

Эта работа идет на увеличение внутренней энергии проводников, т. е. на их нагревание. Совершение этой работы сопровождается исчезновением магнитного поля, которое существовало в соленоиде. Поскольку никаких других изменений в окружающих электрическую цепь телах не происходит, остается заключить, что магнитное поле является носителем энергии, за счет которой и совершается работа А. Таким образом проводник с индуктивностью L, по которому течет ток I, обладает энергией.

,

которая локализована в возбужденном током магнитном поле.

Выразим энергию магнитного поля через величины, характеризующие само поле. Для бесконечного соленоида

L= I=

Подставив L и I в формулу для W , получим

Магнитное поле бесконечного соленоида однородно и сосредоточено внутри соленоида. Разделив W на объем соленоида, получим объемную плотность энергии магнитного поля.

Если магнитное поле неоднородно, плотность тока больше там, где больше H и . Энергию W заключенную в объеме V в случае неоднородного магнитного поля можно вычислить по формуле

I ~ v

L ~ m

m – характеризует инертные свойства тела по отношению к изменению скорости.

L – характеризует инертные свойства контура. по отношению к изменению тока в нем.

22. Ток смещения.

При изучении постоянного тока мы видели, что когда по проводнику проходит ток, то линии тока всегда замкнуты. Если мы рассмотрим цепь с конденсатором, то между пластинами конденсатора заряды не могут перемещаться. Это приводит к тому, что линии тока обрываются у поверхности пластин конденсатора, в результате чего ток проводимости, текущий по проводнику, соединяющему обкладки конденсатора, оказывается разомкнутым. Тем не менее, при рассмотрении колебательного контура считается, что ток в нем течет, правда переменный.

Рассмотрим, что же происходит при прохождении переменного электрического тока по цепи, содержащей конденсатор.

Пусть пластины конденсатора А и В заряжены с поверхностной плотностью

При разряде конденсатора по проводнику (и внутри самих пластин) пойдет ток

Плотность тока j будет равна

Рассмотрим теперь, что происходит в пространстве между пластинами конденсатора.

Мгновенное значение поля внутри конденсатора можно вычислить по мгновенному значению поверхностной плотности заряда.

Вектор D направлен от пластины А к В. При разряде конденсатора  убывает. Следовательно, вектор направлен в сторону, противоположную вектору D, ( от В к А), то есть совпадает по направлению с током проводимости j вне конденсатора.

Численное значение векторов j и одинаково и равно .

Таким образом, линии плотности тока проводимости j и линии вектора сменяют друг друга.

Обозначим

Эту величину Максвелл назвал плотностью тока смещения.

Тогда ток смешения I_см будет равен

где Ф_эл поток вектора электрической индукции D.

Таким образом, оказывается, что линии плотности тока проводимости j вне конденсатора непрерывно переходят в линии плотности тока смещения j_см между пластинами.

Следовательно, непрерывность линий тока в разомкнутой цепи формально оказывается восстановленной, если плотности тока проводимости j в проводниках сопоставлять в диэлектриках плотность тока смещения j_см, определяемого меняющимся по времени электрическим полем.