16. Явление электромагнитной индукции. Закон Фарадея.

В 1831 г. Фарадей открыл, что во всяком замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, ограниченную этим контуром, возникает электрический ток. Это явление называется электромагнитной индукцией, а возникающий ток –индукционным.

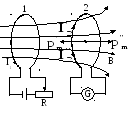
Рассмотрим два контура. В одном включен источник тока и силу тока можно менять реостатом. Во второй контур включен гальванометр.

Ток cоздает магнитное поле, которое пронизывает второй контур. При изменении потока, пронизывающего второй контур в нем возникает индукционный ток. Изменение магнитного поля можно осуществить различными способами:

• Изменяя силу тока 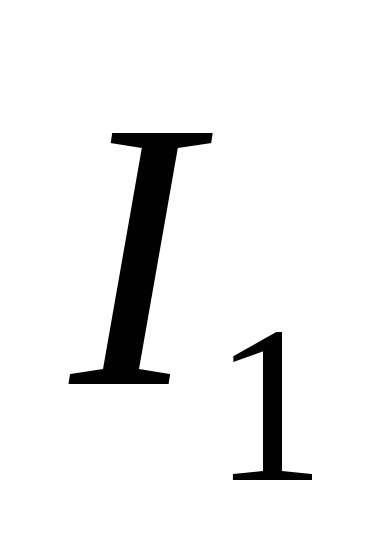, тем самым будет меняться B и ,

• Приближая или удаляя второй контур от первого, будет меняться B, а значит и,.

• Поворачивая второй контур так, чтобы менялся угол между нормалью к контуру и направлением поля ()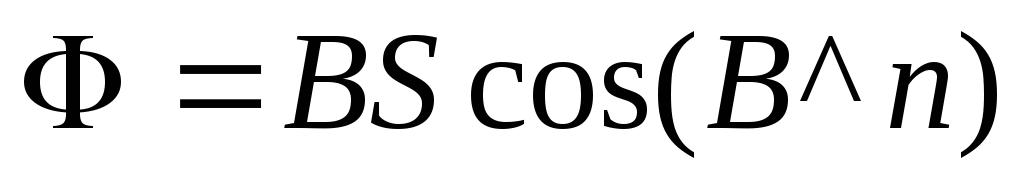

Величина индукционного тока не зависит от способа, которым вызывается изменение потока магнитной индукции , и определяется лишь скоростью изменения , т.е. значением .

Ленц установил правило, с помощью которого можно найти направление индукционного тока. Правило Ленца гласит, что индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей.

При увеличении тока или при приближении второго контура к первому возникает индукционный ток и магнитный момент , магнитное поле которого направлено против внешнего поля, т.е. препятствуют увеличению магнитного потока.

При уменьшении тока или при удалении второго контура возникает индукционный ток и магнитный момент , магнитное поле которого совпадает с направлением внешнего поля, т.е. препятствуют уменьшению магнитного потока.

Согласно закону Ома электрический ток в замкнутой цепи может возникать только в том случае, если в этой цепи появится ЭДС. Поэтому обнаруженный Фарадеем индукционный ток свидетельствует о том, что в замкнутом контуре, находящемся в переменном магнитном поле возникает ЭДС индукции. Дальнейшее исследование показало, что ЭДС электромагнитной индукции в контуре пропорционально изменению магнитного потока сквозь поверхность , ограниченную этим контуром .

(в СИ |к|=1) (1)

Объединим эти формулы с правилом Ленца .По правилу Ленца имеем:

Условились считать ЭДС положительной , если магнитный момент соответствующего ей индукционного тока образует острый угол с линиями магнитной индукции того поля , которое наводит этот ток.

Тогда в случае : а) >0,

б) <0

Сравнивая с формулой (1) получим, что k= -1.

- закон Фарадея. (2)

ЭДС электромагнитной индукции в замкнутом контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность , ограниченную этим контуром .

Если контур состоит из N витков , то ЭДС возникает в каждом витке и результирующая ЭДС будет в N раз больше.

, (3)

где -потокосцепление контура.

17. Вывод закона Фарадея.

Гельмгольц установил, что закон Фарадея является следствием закона сохранения энергии. Покажем это.

Рассмотрим замкнутый проводящий контур в магнитном поле. В контур включен источник тока с ЭДС равной и в нем протекает ток I. В контуре имеется незакрепленный участок АС, который под действием силы Ампера придет в движение. При этом перемещении будет совершаться работа

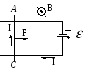Кроме этого будет совершаться работа по преодолению электрического сопротивления R цепи, т.е. на нагревание контура

Полная работа, совершенная за это же время гальваническим элементом

По закону сохранения энергии:

,

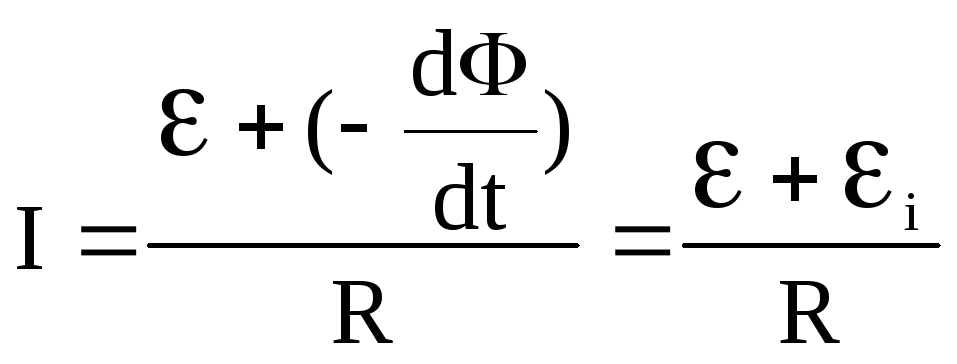Т.о. при изменении магнитного потока, сцепленного с контуром, в последнем возникает добавочная электродвижущая сила.

Выведем теперь формулу для ЭДС индукции на основе элетронной теории.

Э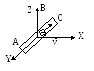ДС электромагнитной индукции возникает не только в замкнутом проводнике с током, но и в отрезке проводника, пересекающем при своем движении линии магнитной индукции.

Пусть прямолинейный отрезок проводника AC длиной l расположен вдоль оси Y и движется в в направлении оси X со скоростью v. Индукция магнитного поля В направлена вдоль оси Z.

На электроны , движущиеся со скоростью v действует сила Лоренца

F=evB

Под действием этой силы электроны будут смещаться к одному из концов отрезка (концуC). Возникает разность потенциалов и электрическое поле внутри проводника с напряженностью E. Со стороны возникшего электрического поля на электроны будет действовать сила qE., направление которой противоположно силе Лоренца. Когда эти силы уравновесят друг друга, то движение электронов прекратится.

Eq=qvB, E=vB

Будем считать возникшее электрическое поле однородным. Тогда

Цепь разомкнута, значит .

Но в проводнике нет гальванического элемента или других источников тока, значит это будет ЭДС индукции

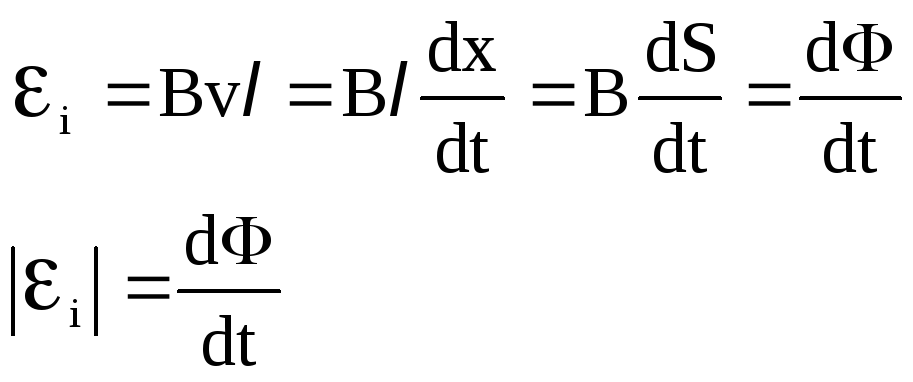
При перемещении в магнитном поле замкнутого проводящего контура ЭДС индукции находится во всех его участках, пересекающих линии магнитной индукции. Алгебраическая сумма этих ЭДС равна общей ЭДС индукции замкнутого контура .