Практична робота №2 Термодинамічні розрахунки імовірності протікання твердофазних реакцій у процесах спікання металургійної сировини

1. Теоретичні передумови

До найважливіших величин, що характеризують хімічні системи, відносяться: внутрішня енергія U, ентальпія Н, ентропія S і енергія Гіббса (ізобарно-ізотермічний потенціал) G [2, с. 81-92; 3, с. 73-83]. Всі ці величини є функціями стану, тобто залежать тільки від стану системи, але не від способу, яким цей стан досягнутий.

При екзотермічних реакціях (тепло виділяється) внутрішня енергія системи зменшується (ΔU<0). Якщо внутрішня енергія системи зростає (ΔU>0) то процес супроводжується поглинанням енергії із зовнішнього середовища (ендотермічна реакція).

Якщо в результаті хімічної реакції система поглинула тепло Q і виконала роботу А, то зміна внутрішньої енергії ΔU=Q-А.

Відповідно до закону збереження енергії, ΔU залежить тільки від початкового й кінцевого стану системи, але не залежить від способу здійснення процесу (реакції). Навпроти, Q і А будуть різнитися залежно від способу здійснення процесу (функцією стану є тільки різниця Q і А, але не кожна з них окремо).

Якщо реакція протікає при постійному об’ємі (ΔV=0, ізохорний процес), то робота розширення системи (А=Р∙ΔV) дорівнює нулю. Якщо при цьому не відбуваються й інші види робіт, наприклад, електрична, то ΔU=Q_V, де Q_V – тепловий ефект реакції (тобто кількість поглиненої системою теплоти), що протікає при постійному об’ємі. Для екзотермічної реакції Q_V<0, для ендотермічної Q_V>0.

Для ізобарного процесу (ΔР=0), більш характерного для хімічних реакцій, зручніше користуватися не U, а Н=U+РΔV.

При постійному тиску ΔН=ΔU+РΔV.

Якщо при цьому ніякі інші роботи не відбуваються, ΔН=Q_Р, де Q_Р – тепловий ефект реакції, що протікає при постійному тиску.

Стандартний стан речовини при даній температурі - його стан у вигляді чистої речовини при нормальному атмосферному тиску 101325 Па, або 760 мм. рт. ст. Стандартні умови протікання реакції - стандартні зміни відповідних величин ΔUº і ΔНº [Дж].

Стандартна ентальпія реакції утворення 1 моля даної речовини із простих речовин звичайно виражається в кДж/моль.

Закон Гесса (1840): Тепловий ефект хімічної реакції залежить тільки від початкового й кінцевого станів речовин, що беруть участь у реакції, і не залежить від проміжних станів процесу. Наслідок: Стандартна зміна ентальпії хімічної реакції дорівнює сумі стандартних ентальпій утворення продуктів реакції за відрахуванням суми стандартних ентальпій утворення вихідних речовин. [Аналогічно для ΔS і ΔG].

Напрямки самовільного протікання хімічних реакцій визначаються спільною дією двох факторів: 1) тенденцією до переходу системи в стан з найменшою внутрішньою енергією (ентальпією); 2) тенденцією до досягнення найбільш імовірного стану, тобто стану, що може бути реалізовано найбільшим числом рівновірогідних способів (мікростанів).

Мірою першої (проявляється при всіх температурах однаковою мірою) тенденції є ΔН(ΔU) - зменшення яких сприяє самовільний плин ізобарного процесу (екзотермічний процес).

Мірою другої (проявляється тим сильніше, чим вище температура) тенденції являється ΔS[Дж/(моль∙К)]=Q_обр./Т. S=k lgW, де k - коефіцієнт пропорційності; W - число рівновірогідних мікроскопічних станів, якими може бути реалізований даний макростан.

Ентропія зростає з підвищенням температури; при переході з кристалічного стану в рідкий й далі в газоподібний; при збільшенні числа газових молекул у ході реакції.

На відміну від ентальпії, ентропія утворення простої речовини не дорівнює нулю.

Функція, що одночасно відбиває вплив обох тенденцій на напрямок протікання хімічних процесів, називається енергією Гіббса: G=H-TS і характеризує максимальну роботу процесу.

Для ізобарно-ізотермічних процесів ΔG= ΔH-TΔS.

При сталості температури й тиску хімічні реакції можуть самовільно протікати тільки в такому напрямку, при якому енергія Гіббса системи зменшується (ΔG<0).

Використовуючи дані, що приводяться в довідниках термодинамічних властивостей речовин, можна розрахувати стандартну зміну цієї функції ΔG (ΔG=ΔН-ТΔS).

В принципі цю характеристику також можна використовувати для оцінки термодинамічної імовірності реакції. Однак до такої оцінки варто підходити з обережністю, тому що стандартні умови (25ºС та 1 атм.) не відповідають реальним умовам протікання процесу, при яких значення ΔGº може істотно відрізнятися від стандартних. Перерахунок стандартних термодинамічних величин на інші вимагає відомостей про теплоємність речовин, що беруть участь у реакції.

Термодинамічна імовірність – число мікростанів (мікророзподілів), якими може здійснюватися розглянутий мікророзподіл [2, c. 70-71].

Число мікророзподілів N часток по n станах (наприклад N часток в n відсіках) виражається формулою:

(2.1)

де N₁, N_2, …, N_n – число часток у першому, другому, n-ному стані (відсіку). Причому N=N₁+N₂+…+N_n...

Обчислимо термодинамічну імовірність макростанів а, б, в, г, д, наведених на рис. 2.1.

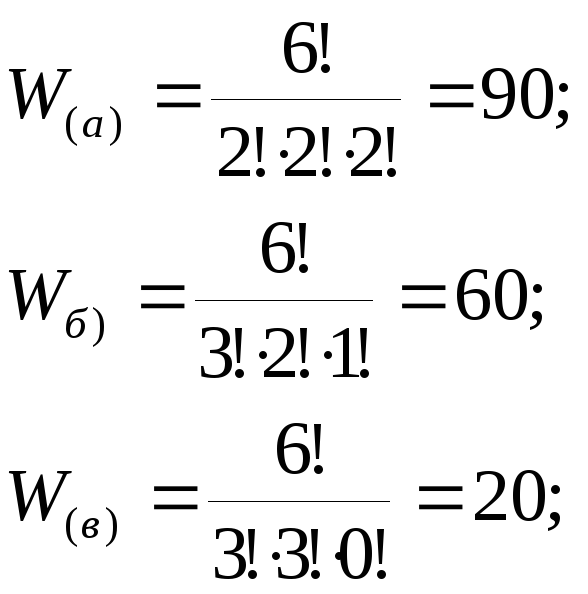
Рис. 2.1. Різні макророзподіли шести часток по трьох станах

Таким чином, найбільшу термодинамічну імовірність має рівномірний розподіл, він може здійснюватися найбільшим числом способів.

Больцман показав, що ентропія системи S може служити характеристикою термодинамічної імовірності даного стану системи W. Зв'язок між ними виражається рівнянням:

(2.2)

де R – універсальна газова постійна;

N_A – число Авогадро;

- постійна Больцмана.

Формула (2.2) відноситься до числа чудових співвідношень, породжених науковою думкою [усього їх три, у тому числі формула Ейлера () і формула Енштейна ()], які зв'язують простим співвідношенням величини, що володіють зовсім різними властивостями, які відносяться до різних матеріальних сутностей [фізичні величини (S, R) з математичною (W)].

, (2.3)

де - модуль десяткового логарифма;

– коефіцієнт пропорційності.

Число е є межа, до якої прагне ( )ⁿ при необмеженому зростанні n; .

Абсолютно достовірною характеристикою імовірності протікання реакції в розглянутих умовах служить істинна зміна енергії Гіббса ΔG, зв'язана зі стандартною зміною ΔGº рівнянням ізотерми хімічної реакції.

У загальному випадку знак ΔG може не збігтися з ΔGº. Знак ΔGº буде збігатися зі знаком ΔG у двох випадках:

1) парціальні тиски складових реакції мало відрізняються від стандартного значення;

2) ΔGº велике за абсолютним значенням (практично більше 40 кДж).

Термодинамічну імовірність протікання реакції варто відрізняти від її практичної імовірності, під якою мають на увазі протікання реакції з помітною швидкістю. Наявність кінетичних труднощів може стати перешкодою до проведення реакції з необхідною швидкістю.