
- •7.Примеры и рекомендации к выполнению элементов расчетной и графической частей курсовой работы
- •7.1.2. Подбор электродвигателя
- •7.1.3. Разбивка общего передаточного числа привода по передачам
- •7.1.4. Подготовка исходных данных для расчета элементов привода
- •2. Расчет цилиндрической косозубой зубчатой передачи [2]
- •2.1.Установление основных данных
- •2.2. Коэффициенты режима (п.2.5.3.3.С.8)
- •Допускаемые контактные напряжения при расчете на сопротивление усталости (п.2.5.3.2.)
- •2.4.Определение основных размеров зубчатой пары
- •2.5. Определение геометрии зацепления
- •2.6 Диаметры зубчатых колес
- •4.2. Расчет на прочность при максимальной нагрузке по формуле (57)
2.2. Коэффициенты режима (п.2.5.3.3.С.8)
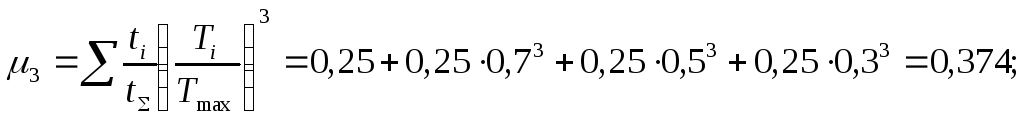
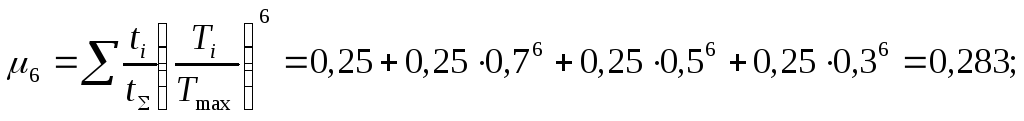

Допускаемые контактные напряжения при расчете на сопротивление усталости (п.2.5.3.2.)
2.3.1.Суммарные числа циклов по формуле (6б), с.8
![]() ;
;
![]() .
.
.2.3.2. Эквивалентные числа циклов по формуле (8) с.9
![]() ;
;
![]() .
.
2.3.3. Базовые числа циклов по формуле (5) с.8.
![]() ;
;
![]() .
.
2.3.4. Коэффициенты долговечности (п. 2.5.3..)
Поскольку![]() >
>![]() ,
а
,
а![]() >
>![]() ,
то
,
то
![]() >
>![]() ,а
,а
![]() >
>![]() .
.
Если при расчете![]()
![]() ,
а
,
а![]()
![]() ,
то принимается 6-ая степень корня.
,
то принимается 6-ая степень корня.
2.3.5. Пределы контактной выносливости (табл.1,с.5..)
![]() МПа;
МПа;
![]() МПа.
МПа.
2.3.6. Коэффициенты
запаса (п. 2.5.2. с.8..): шестерни -
![]() ,
колеса -
,
колеса -![]() .рис.7
с.17
.рис.7
с.17
2.3.7. Допускаемые напряжения шестерни и колеса по формуле (2) с.7.
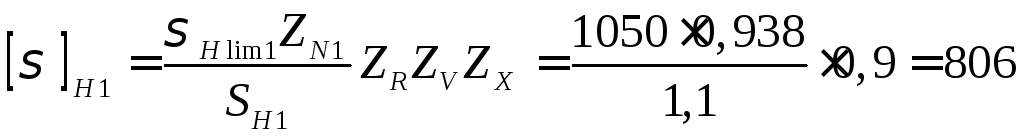 МПа;
МПа;
 МПа,
МПа,
где
принято
![]() ,
для передач общего назначения.
,
для передач общего назначения.
2.3.8. Расчетное допускаемое напряжение (п. 2.5..)
![]() МПа;
МПа;
![]() МПа.
МПа.
За
расчетное принимаем меньшее, т.е.
![]() МПа.
МПа.
2.4.Определение основных размеров зубчатой пары
2.4.1. Начальный диаметр шестерни по формуле (9) с.9.
 мм.
мм.
2.4.2. Расчетная ширина колеса по формуле (10) с.10
![]() мм.
мм.
2.4.3. Межосевое расстояние по п 2.6.2. (11) с.10
![]() мм.
мм.
Принимаем
стандартное межосевое расстояние
![]() мм. Поскольку расчетное межосевое
расстояние отличается от стандартного,
уточняем ширину колеса по формуле
мм. Поскольку расчетное межосевое
расстояние отличается от стандартного,
уточняем ширину колеса по формуле
 мм.
мм.
Принимаем ширину
колеса
![]() мм,
ширину шестерни
мм,
ширину шестерни![]() мм.
мм.
2.5. Определение геометрии зацепления
2.5.1. Модуль (п.2.6.3.1.)
![]() мм.
мм.
Согласно
табл. 5 . в указанном диапазоне находятся
модули: 1,25; 1,5; 1,75; 2,0; 2,25 и 2,5. Выбираем
модули, соответствующие первому
предпочтительному ряду: 1,5; 2,0 и 2,5.
Расчет ведем для трех вариантов.
Ориентировочно принимаем
![]() .
Результаты сведем в таблицу.
.
Результаты сведем в таблицу.
Таблица 2.
|
Параметры, формулы, размерность |
Значения параметров | ||
|
Модуль
зуба
|
1,5 |
2,0 |
2,5 |
|
Число
зубьев шестерни с округлением до
целого числа
|
27 |
20 |
16 |
|
Число
зубьев колеса с округлением до целого
числа
|
135 |
100 |
80 |
|
Фактическое
передаточное число
|
5 |
5 |
5 |
|
Угол
наклона зуба ( с точностью до секунд
или 4-го знака после запятой) |
13,59050 |
16,26020 |
16,26020 |
|
Осевой
шаг
|
20,05 |
22,44 |
28,05 |
|
Коэффициент
осевого перекрытия
|
1,55 |
1,38 |
1,11 |
Примечание.Если число зубьев Z<17
(как в нашем случае при
![]() ),
то следует выполнить проверку на
возможность подрезания зуба по формуле[15]
),
то следует выполнить проверку на
возможность подрезания зуба по формуле[15]
![]()
![]()
Так
как Zmin<16,
подрезания зуба не будет.![]()
Передаточные числа
во всех вариантах одинаковы и равны
заданному, а
![]() >1,
т.е. варианты примерно равнозначны.
Выбираемm=1,5
мм, так как в этом случае
>1,
т.е. варианты примерно равнозначны.
Выбираемm=1,5
мм, так как в этом случае![]() меньше, чем приm=2
и
меньше, чем приm=2
и
![]() ,
следовательно осевая сила в зацеплении
также будет меньше, а коэффициент осевого
перекрытия
,
следовательно осевая сила в зацеплении
также будет меньше, а коэффициент осевого
перекрытия![]() наибольший. Это значит, что передача
будет работать плавней.
наибольший. Это значит, что передача
будет работать плавней.
2.6 Диаметры зубчатых колес
2.6.1. Делительные диаметры колес (23)
 мм;
мм;
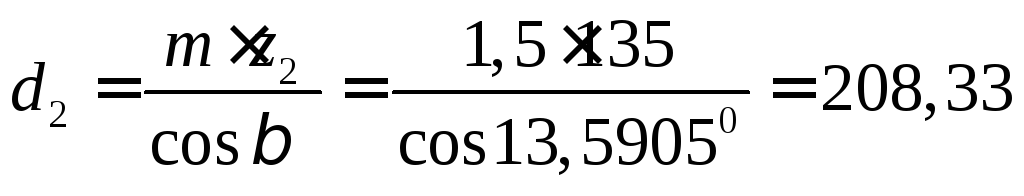 мм.
мм.
![]() - проверка.
- проверка.
2.6.2.Диаметры вершин зубьев (24)
![]() мм;
мм;
![]() мм.
мм.
Здесь
коэффициенты смещения шестерни и колеса
![]() и – коэффициент воспринимаемого
смещения
и – коэффициент воспринимаемого
смещения![]()
2.6.3. Диаметры впадин по формуле (25)
![]() мм;
мм;
![]() мм.
мм.
2.6.4
Начальные диаметры совпадают с делительными, так как колеса выполнены без смещения
![]() мм ;
мм ;
![]() мм
мм
2.6.5.
Уточнение коэффициента относительной ширины зубчатого венца по формуле (27)
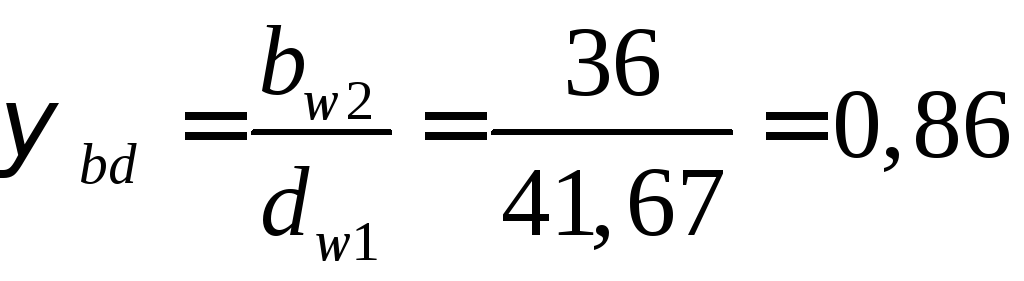
2.7.Коэффициент торцового перекрытия по формуле (28а)

![]()
2.8.Суммарный коэффициент перекрытия по формуле (29)
![]()
2.9 Размеры для контроля взаимного положения разноименных профилей
2.9.1 Постоянная хорда, выраженная в долях модуля по формуле (30)
![]()
2.9.2 Постоянная хорда по формуле (31)
![]() мм.
мм.
2.9.3. Высота до постоянной хорды по формуле (32)
![]()
![]() мм.
мм.
2.10. Скорость и силы в зацеплении
2.10.1. Окружная скорость по формуле (33)
![]() м/c.
м/c.
2.10.2. Окружная сила по формуле (34)
![]() Н.
Н.
2.10.3. Радиальная сила по формуле (35)
![]() Н.
Н.
2.10.4. Осевая сила по формуле (36)
![]() Н.
Н.
2.11. Размеры, определяющие прокаливаемость по п. 2.9.
Колесо -
![]() мм.
мм.
Кривые прокаливаемости (рис. 7) подтверждают возможность получения у выбранного материала колеса необходимой твердости.
3. Проверочный расчет по контактным напряжениям
3.1. Проверочный расчет на сопротивление усталости
Действительное контактное напряжение определяется по формуле (37) и сравнивается с допускаемым напряжением . Ниже формулы приведены данные для определения коэффициентов нагрузки, которые необходимы для этого расчета.

![]() МПа
МПа
![]() МПа.
МПа.
Условие прочности удовлетворяется.
3.1.1. Коэффициент,
учитывающий форму сопряженных поверхностей
зубьев в полюсе зацепления по рис. 9
![]()
3.1.2. Коэффициент,
учитывающий суммарную длину контактных
линий для косозубых колес при
![]() по формуле (40а)
по формуле (40а)
![]() .
.
3.1.3. Коэффициент нагрузки по формуле (41)
![]()
3.1.3.1. Коэффициент внешней динамической нагрузки по п. 3.1.3.1.
Принимаем
![]() ,
так как циклограмма нагружения задана.
,
так как циклограмма нагружения задана.
3.1.3.2. Коэффициент, учитывающий динамическую нагрузку в зацеплении
![]() при
при
![]() м/с, твердости одного из колес меньше
м/с, твердости одного из колес меньше![]() и 8-й степени точности (табл. 7).
и 8-й степени точности (табл. 7).
3.1.3.3. Коэффициент,
учитывающий неравномерность распределения
нагрузки по длине контактных линий при
![]() будет
будет![]() (см. рис. 1).
(см. рис. 1).
3.1.3.4. Коэффициент, учитывающий неравномерность распределения нагрузки по парам зубьев по формуле (42)
![]() .
.
Здесь
![]() по формуле (43а), так как твердость колеса
меньше
по формуле (43а), так как твердость колеса
меньше![]() (Значение коэффициента
(Значение коэффициента![]() находится в допустимых предела
находится в допустимых предела![]() );
);![]() - коэффициент, учитывающий приработку
зубьев (по рис. 10). Подставляем найденные
значения в формулу (37) и находим
- коэффициент, учитывающий приработку
зубьев (по рис. 10). Подставляем найденные
значения в формулу (37) и находим![]()
3.1.4. Уточнение допускаемого контактного напряжения
3.1.4.1. Коэффициент,
учитывающий влияние исходной шероховатости
поверхностей зубьев. При
![]()
![]() (п. 2.5.4.).
(п. 2.5.4.).
3.1.4.2. Коэффициент,
учитывающий влияние окружной скорости.
При
![]() <5
- м/c
<5
- м/c
![]() (2.5.5.).рис.2
(2.5.5.).рис.2
3.1.4.3.Коэффициент,
учитывающий размеры зубчатого колеса.
При
![]() мм -
мм -![]() (п. 2.5.6.).
(п. 2.5.6.).
Допускаемые напряжения шестерни и колеса по формуле (2)
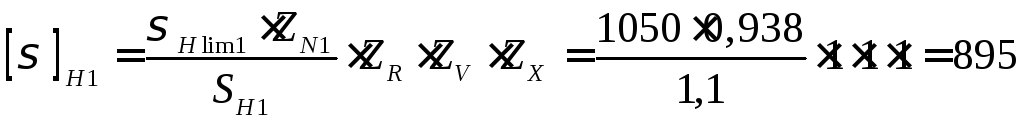 МПа;
МПа;
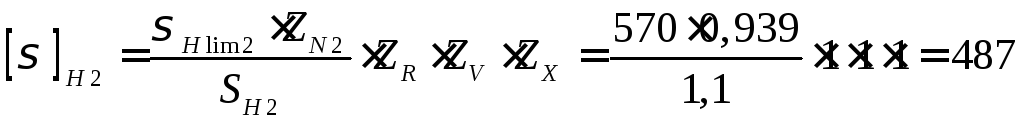 МПа.
МПа.
Расчетное допускаемое напряжение по формуле (3)
![]() МПа;
МПа;
![]() МПа.
МПа.
За расчетное
принимаем меньшее, т.е.
![]() МПа.
МПа.
3.2. Проверочный расчет на контактную прочность при действии максимальной нагрузки по формуле (44)
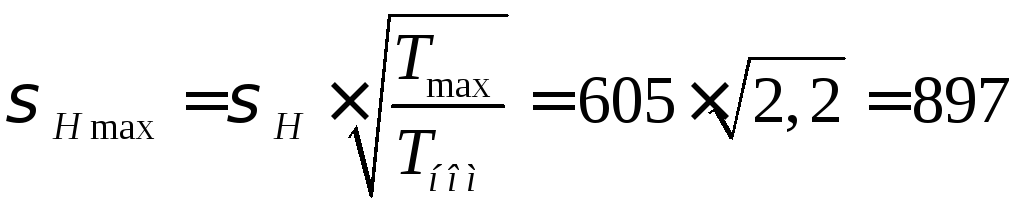 МПа <
МПа <![]() МПа,
МПа,
где
![]() МПа - допускаемые контактные напряжения
по табл. 1;
МПа - допускаемые контактные напряжения
по табл. 1;![]() МПа - предел текучести материала колеса
по рис. 11. ,при
МПа - предел текучести материала колеса
по рис. 11. ,при![]() =250
=250
4. Проверочный расчет по напряжениям изгиба
4.1.Расчет на сопротивление усталости по п. 4.1.
При расчете следует определить наиболее слабый элемент
Поскольку
![]() >
>![]() ,
то проверку ведем для шестерни, как
более слабому элементу. Для нее по
формуле ( 45) предварительно определив
коэффициенты нагрузки и допускаемые
напряжения, которые приводятся ниже.
,
то проверку ведем для шестерни, как
более слабому элементу. Для нее по
формуле ( 45) предварительно определив
коэффициенты нагрузки и допускаемые
напряжения, которые приводятся ниже.

![]() МПа
МПа
Условие прочности выполняется.
![]() 4.1.1.
Коэффициент нагрузки по формуле (46)
4.1.1.
Коэффициент нагрузки по формуле (46)
![]()
4.1.1.1. Коэффициент, учитыващий внешнюю динамическую нагрузку
Принимаем
![]() ,
так как циклограмма нагружения задана.
,
так как циклограмма нагружения задана.
4.1.1.2. Коэффициент,
учитывающий динамическую нагрузку в
зацеплении
![]() при
при![]() м/с, твердости одного из колес меньше
м/с, твердости одного из колес меньше![]() и 8-й степени точности (табл. 8).
и 8-й степени точности (табл. 8).
4.1.1.3. Коэффициент,
учитывающий неравномерность распределения
нагрузки по длине контактных линий при
![]() ,
,![]() (по рис. 12).
(по рис. 12).
4.1.1.4. Коэффициент, учитывающий неравномерность распределения нагрузки по парам зубьев по формуле (47)
![]() .
.
4.1.2. Коэффициенты,
учитывающие форму зуба и концентрацию
напряжений, для колес с наружным
зацеплением по рис. 13 при
![]() ,формула
(17)
,формула
(17)![]() и
и![]() -
-![]() и
и![]() .
.
4.1.3. Коэффициент, учитывающий влияние угла наклона зуба по формуле (48)
 .
.
4.1.4. Коэффициент,
учитывающий перекрытие зубьев по формуле
(49а), так как![]() .
.
![]()
.
4.1.5. Допускаемые напряжения при расчете на сопротивление усталости при изгибе для шестерни и колеса по формуле (50)
![]() МПа;
МПа;
![]() МПа.
МПа.
4.1.5.1. Предел выносливости при изгибе по формуле (51)
![]() МПа;
МПа;
![]() МПа.
МПа.
4.1.5.2. Предел
выносливости при изгибе, соответствующий
базовому числу циклов по табл. 1:
![]() МПа для стали
МПа для стали![]() при сквозной закалке
при сквозной закалке![]() ;
;![]() МПа для улучшенной стали
МПа для улучшенной стали![]() .
.
4.1.5.3. Коэффициент, учитывающий способ получения заготовки
При штампованной
заготовке
![]() .
.
4.1.5.4. Коэффициент, учитывающий влияние шлифования переходной поверхности по п. 4.1.5.4.
При шлифованной
поверхности
![]() ,
,![]() .
Табл.1
.
Табл.1
4.1.5.5. Коэффициент, учитывающий влияние деформационного упрочнения по п. 4.1.5.5.
При отсутствии
упрочнения
![]() .
.
4.1.5.6. Коэффициент, учитывающий влияние характера приложения нагрузки по п. 4.1.5.6.
При односторонней
нагрузке
![]() .
.
4.1.6. Коэффициент запаса при изгибе по табл. 1
![]() ;
;![]() .
.
4.1.7. Коэффициенты долговечности по п. 4.1.7.
Поскольку![]() >
>![]() ,
а
,
а![]() >
>![]() ,
то
,
то![]() .
или рассчитать
.
или рассчитать
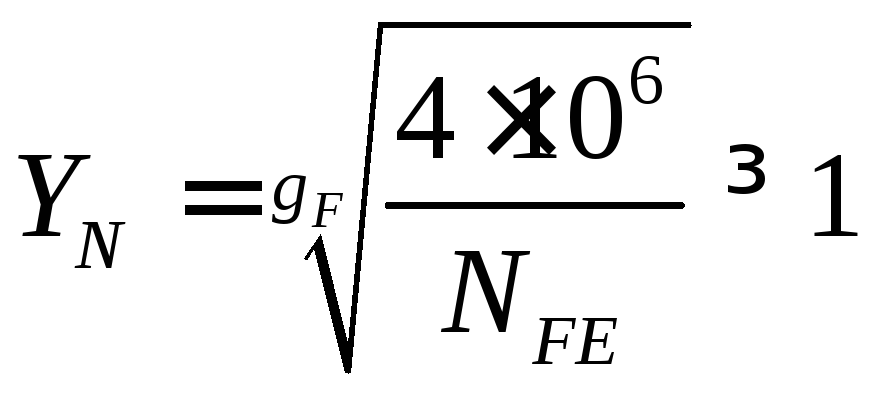
Для нашего случая
![]() ,
так как колесо и шестерня шлифованные
и имеют однородную структуру зубьев.
,
так как колесо и шестерня шлифованные
и имеют однородную структуру зубьев.
Здесь эквивалентные числа циклов при изгибе по формуле (53) с учетом п. 2.5.3.2. настоящего примера
![]() ;
;
![]() .
.
Коэффициенты
режима работы по формуле (54а), так как
![]() будут
будут
 .
.
Коэффициент, учитывающий градиент напряжений по формуле (55)
![]() .
.
4.1.9. Коэффициент
![]() ,
учитывающий шероховатость переходной
поверхности по п. 4.1.9.
,
учитывающий шероховатость переходной
поверхности по п. 4.1.9.
При шлифовании и
зубофрезеровании с шероховатостью не
более
![]() мкм
мкм![]() .
.
4.1.10. Коэффициенты, учитывающие размеры зубчатого колеса по формуле (56)
![]() ;
;
![]() .
.

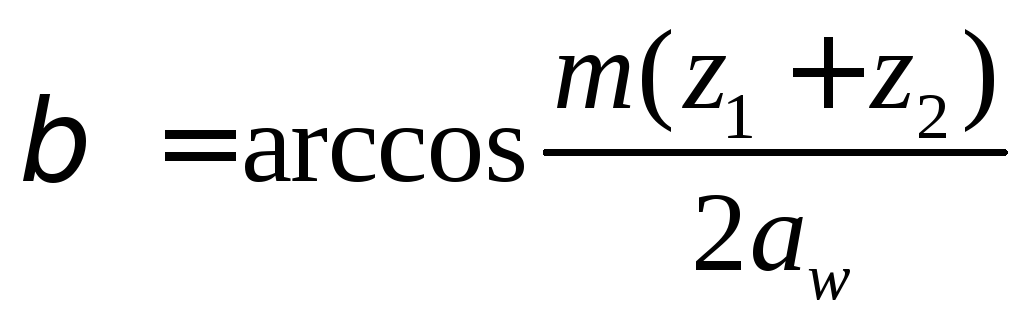
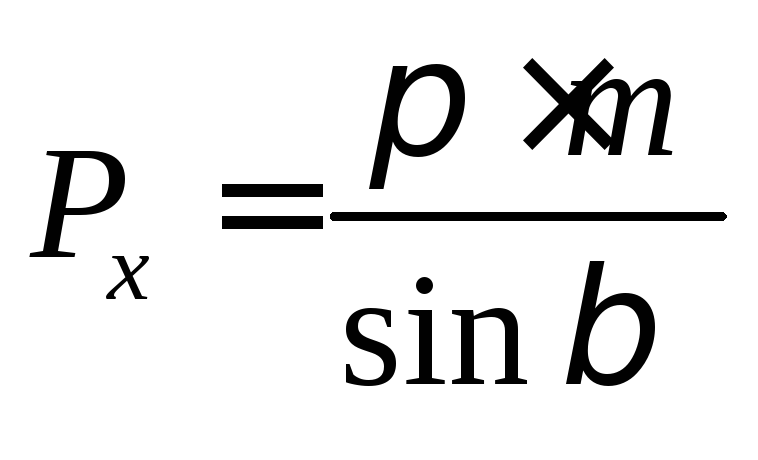 ,
мм
,
мм