Ряды динамики. Статистическое изучение динамики
Ряд динамики, хронологический ряд, динамический ряд, временной ряд – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления.
Каждый ряд динамики включает два обязательных элемента: во-первых, время и, во-вторых, конкретное значение показателя, или уровень ряда.
Несопоставимость уровней ряда может возникнуть вследствие:
-
изменения единиц измерения и единиц счета;
-
влияния методологии учета или расчета показателей;
-
различия периодизации динамики;
Процесс выделения однородных этапов развития рядов динамики носит название периодизации динамики.
-
различия уровней в экономическом смысле;
-
изменения территориальных границ областей;
-
р
 азличного
круга охватываемых объектов.
азличного
круга охватываемых объектов.
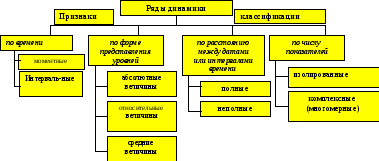
Рис. 18 - Классификация рядов динамики
|
Для интервальных рядов с равными периодами времени:
где
n – число уровней.
|
Для интервальных рядов с неравными периодами времени (датами):
где
|
Для моментных рядов с равноотстоящими моментами:
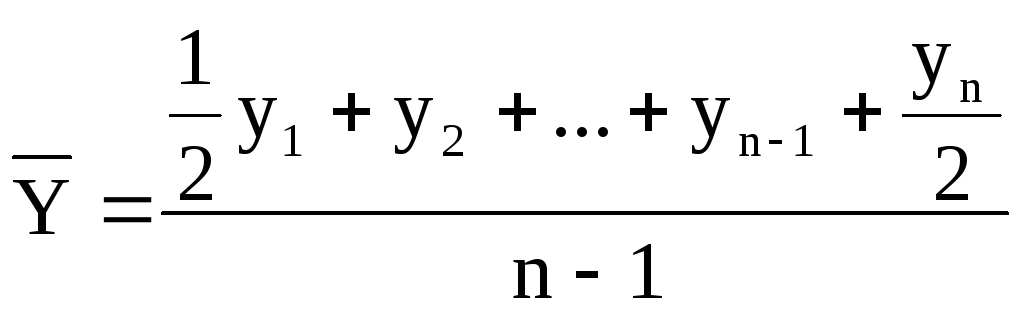 (10.3)
(10.3)
(средняя хронологическая).
Для моментного ряда с неравными интервалами:
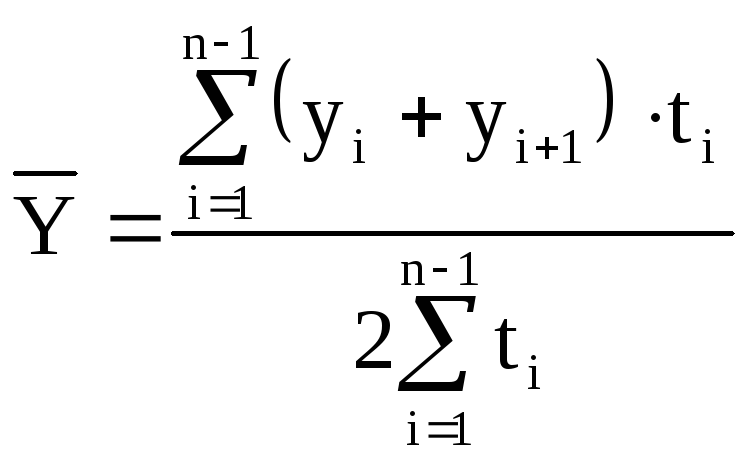 ,
(10.4)
,
(10.4)
где yi, yn – уровни рядов динамики, ti – длительность интервала времени между уровнями.
Показатели рядов динамики
|
Вид показателя |
Базисные |
Цепные |
Средние |
|
Абсолютный
прирост ( |
|
(n - 1) – количество субпериодов |
|
|
Коэффициент роста (Кр) |
Кр
б=
Кр
б= где П – произведение |
Кр
ц= |
|
|
Темп роста (Тр) |
Тр
б=( |
Трц= |
|
|
Коэффициент прироста (Кпр)
|
Кпр б= К рб-1
Кпр
б=
Кпр
б= |
Кпр
ц= Кр
ц
Кпр
ц=
Кпр
ц= |
|
|
Темп прироста (Тпр) |
Тпр
б= Кпр
б·
Тпр
б= Трб
|
Тпр
ц = Кпр
ц·
Тпр
ц = Тр
ц -
|
|
|
Абсолютное
значение одного процента прироста
А1% |
Ац=0,01Yi-1
Ац= |
||
Тренд – основная тенденция развития динамического ряда; (к увеличению либо снижению его уровня).
Методы анализа основной тенденции (тренда) в рядах динамики
Одной из задач, возникающих при анализе рядов динамики, является установление закономерности изменения уровней изучаемого показателя во времени.
В этих случаях для определения основной тенденции развития явления, достаточно устойчивой на протяжении данного периода, используют особые приемы обработки рядов динамики.
Выявление основной тенденции развития (тренда) называется в статистике также выравниванием временного ряда, а методы выявления основной тенденции - методами выравнивания.
Один из наиболее простых приемов обнаружения общей тенденции развития явления - укрупнение интервала динамического ряда.
Выявление основной тенденции может быть осуществлено также методом скользящей средней.
При
аналитическом
выравнивании ряда
динамики закономерно изменяющийся
уровень изучаемого показателя оценивается
как функция времени
![]() ,
где
,
где
![]() - уровни динамического ряда, вычисленные
по соответствующему аналитическому
уравнению на момент времени t.
- уровни динамического ряда, вычисленные
по соответствующему аналитическому
уравнению на момент времени t.
Выбор формы кривой может осуществляться и на основе принятого критерия.
Аналитическое выравнивание ряда динамики по прямой, т.е. аналитическое уравнение вида:
Yt=b0+b1t,
где t - порядковый номер периодов или моментов времени.
Параметры b0 и b1 прямой рассчитываются по методу наименьших квадратов (МНК). Система нормальных уравнений в данном случае имеет вид:
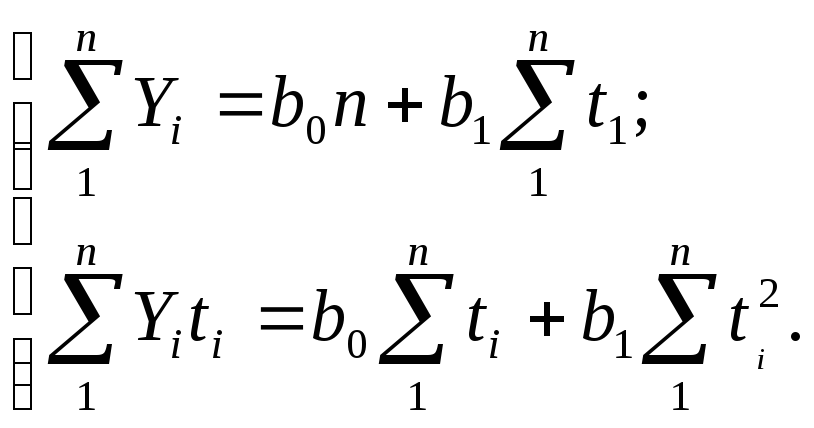
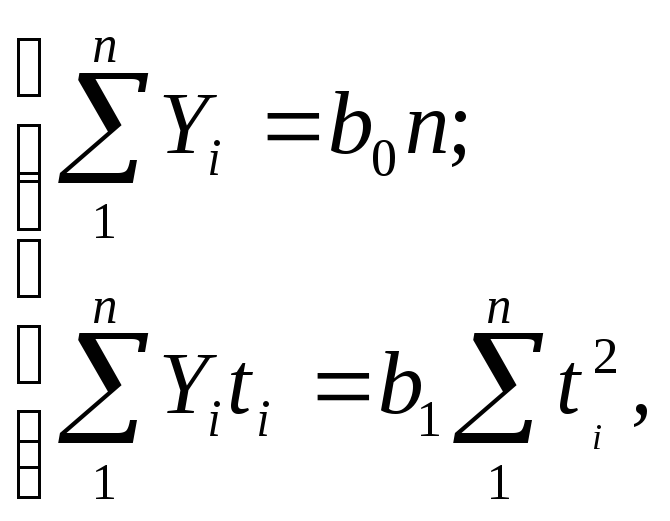 откуда
откуда
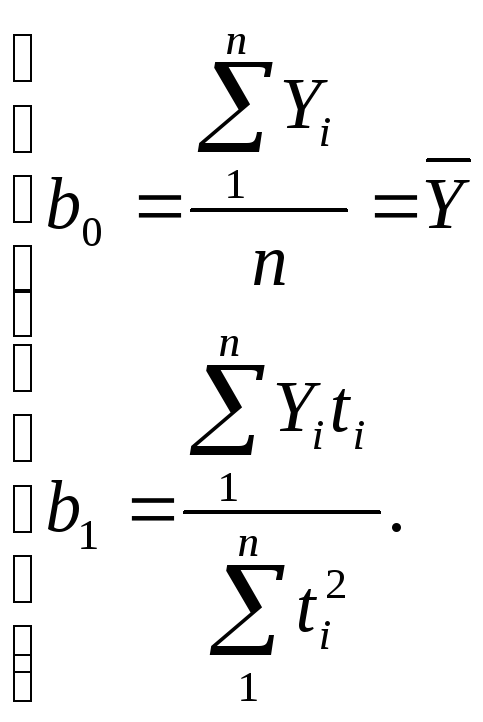
Продление в будущее тенденции, наблюдавшейся в прошлом, носит название экстраполяции. Возможность экстраполяции обеспечивается двумя обстоятельствами:
1) общие условия, определяющие тенденцию развития в прошлом, не претерпевают существенных изменений в будущем;
2) тенденция развития явления характеризуется тем или иным аналитическим уравнением. Общая тенденция развития может быть охарактеризована с помощью содержательного экономического анализа.
Для выравнивания может использоваться парабола второго порядка:
![]() = b0
+ b1
t
+ b2
t
2.
= b0
+ b1
t
+ b2
t
2.
Система нормальных уравнений для нахождения параметров уравнения параболы (при соблюдении принципа отсчета от условного начала) будет иметь вид:
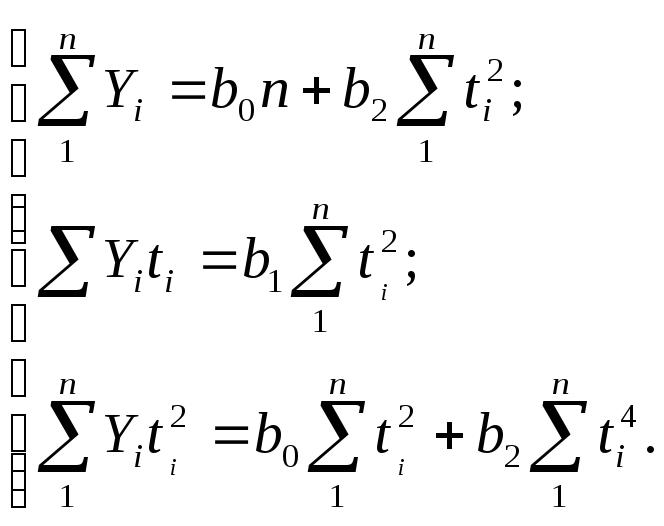
Методы выявления сезонной компоненты
Для выявления сезонных колебаний обычно берут данные за несколько лет, распределенные по месяцам. Данные за несколько лет (обычно не менее трех) берутся для того, чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года. Если ряд динамики не содержит ярко выраженной тенденции в развитии, то индексы сезонности вычисляются непосредственно по эмпирическим данным без их предварительного выравнивания.
Для
каждого месяца рассчитывается средняя
величина уровня, за три года
![]() ,
затем из них рассчитывается среднемесячный
уровень для всего ряда
,
затем из них рассчитывается среднемесячный
уровень для всего ряда
![]() и в заключении определяется процентное
отношение средних для каждого месяца
к общему среднемесячному уровню ряда,
то есть:
и в заключении определяется процентное
отношение средних для каждого месяца
к общему среднемесячному уровню ряда,
то есть:
![]() .
(10.6)
.
(10.6)
![]() ;
(10.7)
;
(10.7)
![]() (10.8)
(10.8)
где n – число одноименных периодов.
В общем виде формулу расчета индекса сезонности данным способом можно записать так:
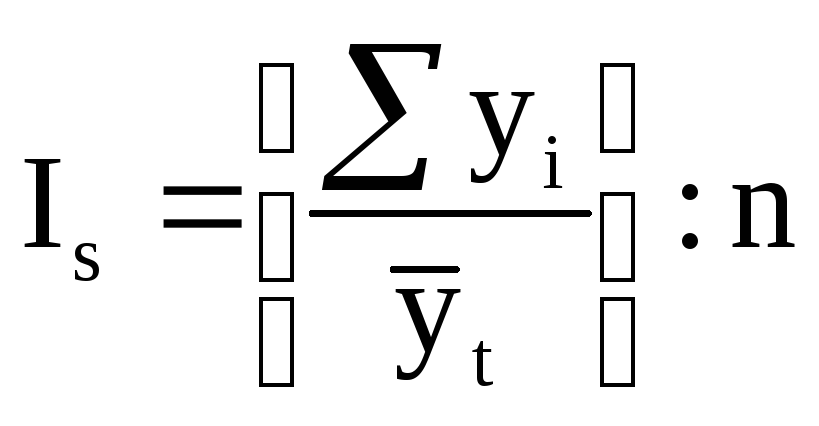 .
(10.9)
.
(10.9)
Индексы
«Индекс» в переводе с латинского – указатель или показатель. В статистике индексом называют показатель относительного изменения данного уровня исследуемого явления по сравнению с другим его уровнем, принятым за базу сравнения.
В дальнейшем изложении будут использоваться следующие общепринятые обозначения:
|
i – индивидуальный индекс; |
I – сводный индекс; |
|
z – себестоимость; |
p – цена; |
|
q – количество; |
Е–экономия, |
|
r – урожайность; |
s – посевная площадь; |
|
( R* s )- валовой сбор, |
Z*q–затраты на производство, |
|
1 – текущий период; |
0 – базисный период. |
индивидуальный индекс:
ip
=
![]() - индекс цены,
- индекс цены,
где р1 – цена товара в текущем периоде; р0 – цена товара в базисном периоде;
iq
=
![]() - индекс физического объёма реализации;
- индекс физического объёма реализации;
ipq
=
![]() - индекс товарооборота
- индекс товарооборота
Агрегатные индексы
сводный индекс товарооборота:
Ipq
=
![]() (11.3)
(11.3)
сводный индекс цен (по методу Пааше):
Ip
=
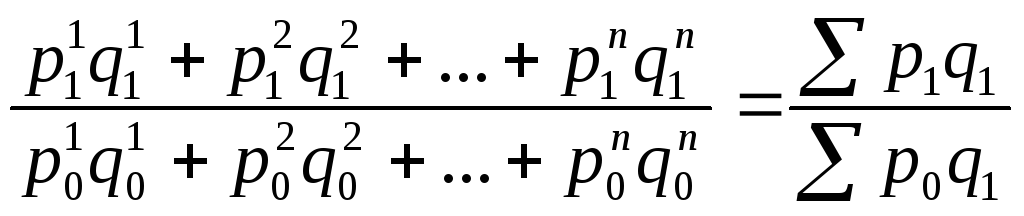 .
(11.4)
.
(11.4)
Разность числителя и знаменателя будет отражать величину экономии (если знак ““) или перерасхода («+») покупателей от изменения цен:
Е = p1q1 – p0q1. (11.5)
сводный индекс физического объёма продукции
Iq
=
![]() .
(11.6)
Ip*Iq
= Ipq.
(11.7)
.
(11.6)
Ip*Iq
= Ipq.
(11.7)
Ipq – индекс стоимости продукции;
Ip – индекс оптовых цен;
Iq – индекс физического объёма продукции.
Взаимосвязь между этими индексами остаётся прежней:
Ip*Iq = Ipq. (11.8)
Индивидуальный индекс себестоимости характеризует изменение себестоимости отдельного вида продукции в текущем периоде по сравнению с базисным.
сводный индекс себестоимости
Iz
=
![]() .
(11.9)
.
(11.9)
Е = z1q1 – z0q1. (11.10)
Индекс физического объёма продукции, взвешенный по себестоимости
Iq
=
![]() (11.11)
(11.11)
Индекс затрат на производство
Izq
=
![]() (11.12)
(11.12)
Все три индекса взаимосвязаны между собой: Iz*Iq = Izq. (11.13)
Ir*Is
= Irs.
(11.14) или
![]() .
(11.15)
.
(11.15)
Сводные индексы в средней арифметической и средней гармонической формах
![]() .
(11.16)
.
(11.16)
сводный индекс цен в данном случае будет выражен в форме средней гармонической:
Ip
=
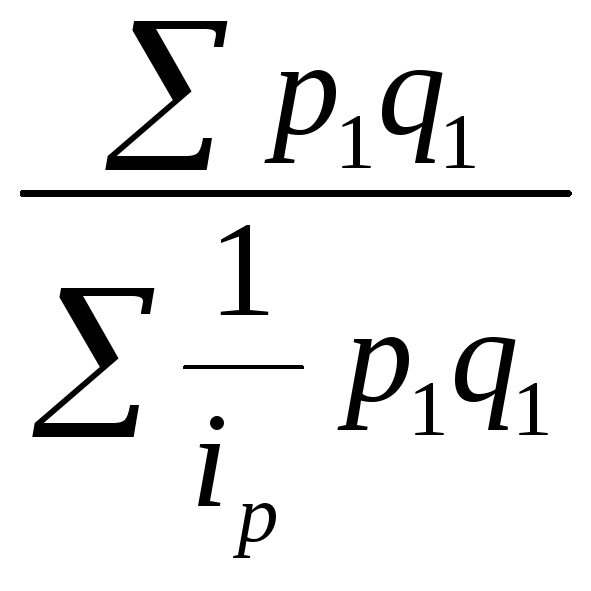 .
(11.17)
.
(11.17)
При расчёте сводного индекса товарооборота можно использовать среднеарифметическую форму. q1 p0 = iq q0 p0. (11.18)
Iq
=
![]() (12.19)
(12.19)
Системы индексов
В зависимости от информационной базы и целей исследователя индексная система может строиться в четырёх вариантах.
А. Цепные индексы цен с переменными весами:
Ip1/0
=
![]() Ip2/1
=
Ip2/1
=
![]() …
…![]() =
=
![]()
Б. Цепные индексы цен с постоянными весами:
Ip1/0
=
![]() Ip2/1
=
Ip2/1
=
![]() …Ipn/n-1
=
…Ipn/n-1
=
![]()
В. Базисные индексы цен с переменными весами:
Ip1/0
=
![]() Ip2/0
=
Ip2/0
=
![]() …Ipn/0
=
…Ipn/0
=
![]()
Г. Базисные индексы цен с постоянными весами:
Ip1/0
=
![]() Ip2/0
=
Ip2/0
=
![]() …Ipn/0
=
…Ipn/0
=
![]()
Индексы системы “Б” по своей природе мультипликативны, т.е. последовательное произведение этих индексов приводит к сводному индексу цен за весь рассматриваемый период (система «Г»).
Территориальные индексы
сводный (общий) индекс цен
![]() =
=
![]() (11.20)
(11.20)
Разность между числителем и знаменателем формулы (11.20) отображает сумму экономического эффекта от различия цен в данных городах:
![]() -
-
![]() .
(11.21)
.
(11.21)
![]() =
=
![]() .
(11.22)
.
(11.22)
Сопоставлением в разности числителя и знаменателя индекса (E M/K ) определяется сумма экономического эффекта от различия в уровнях цен по данным регионам:
E
M/K
=
![]() -
-
![]() .
(11.23)
.
(11.23)
q = q к + q м (11.24)
сводного (общего) индекса цен при анализе изменения цен в городе К по сравнению с городом М следующая:
I
p
к/м
=
![]() .
(11.25)
.
(11.25)
В сводных (общих) территориальных индексах физического объема
![]() =
=
![]() .
(11.26)
.
(11.26)
средние цены по изучаемым регионам (городам) определяются методом средней взвешенной.
![]() =
=
![]() .
(11.27)
.
(11.27)
При многосторонних сравнениях выбор базы сравнения и весов-соизмерителей индексируемых величин предопределяется конкретными целями анализа. При сопоставлениях качественных показателей по ряду регионов соответственно расширяются границы территории, на уровне которых фиксируются веса-соизмерители.
Индексы переменного и постоянного состава
Взаимосвязанные индексы применяются для изучения влияния структурных сдвигов на изменение социально-экономических явлений. В таком анализе индексы находятся во взаимосвязи со средними величинами.
Из формулы средней
![]() =
=
![]() :
:
![]() .
(11.29)
.
(11.29)
следует, что на среднюю величину оказывает влияние как значение осредняемого признака xi , так и численность отдельных вариантов изучаемой совокупности fi .
Это
выполняется с помощью системы
взаимосвязанных индексов, в которой
индекс изменения средней величины I![]() выступает как произведение индекса в
неизменной структуре Ix
на индекс, отображающий влияние изменения
структуры явления на динамику средней
величины I
стр
.
выступает как произведение индекса в
неизменной структуре Ix
на индекс, отображающий влияние изменения
структуры явления на динамику средней
величины I
стр
.
В общем виде эта зависимость записывается так:
I![]() =
Ix
* I
стр.
(11.30)
=
Ix
* I
стр.
(11.30)
При этом
1)
I
![]() =
=![]() :
:
![]() =
=![]() :
:
![]() (11.31)
(11.31)
Индекс (11.31) называется индексом переменного состава, так как в качестве весов-соизмерителей в нем выступает состав продукции (товаров) текущего fi и базисного fо периодов;
2)
Ix
= =![]() :
:
![]() =
=
![]() .
(11.32)
.
(11.32)
Индекс (11.32) называется индексом постоянного (фиксированного) состава, так как в качестве весов-соизмерителей выступает состав продукции (товаров) текущего периода f1;
3)
I
стр
=![]() :
:
![]() (11.33)
(11.33)
В индексе (11.33) изменяются лишь веса-соизмерители f1 и fо. Поэтому данный индекс отображает влияние структурных сдвигов на изучаемый показатель.
Выборочное наблюдение

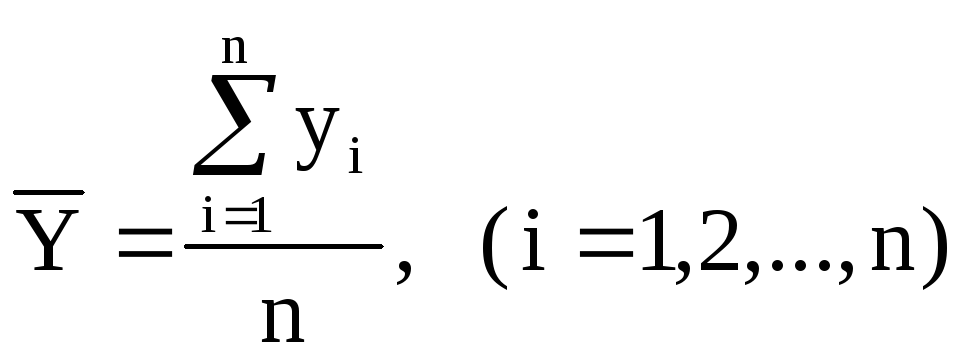 ,
(10.1)
,
(10.1)