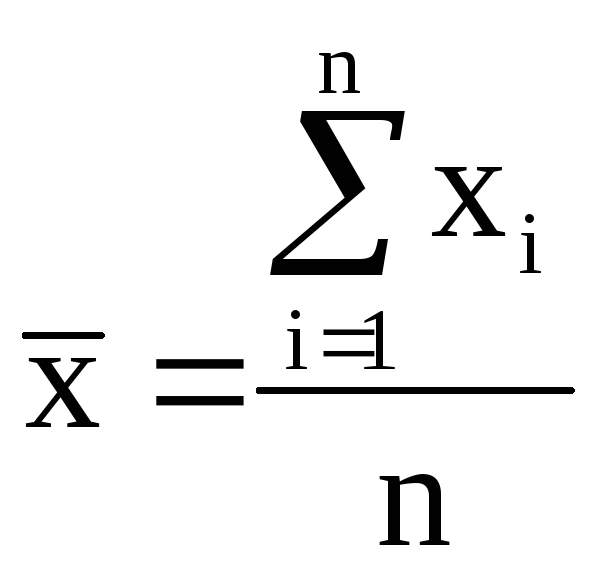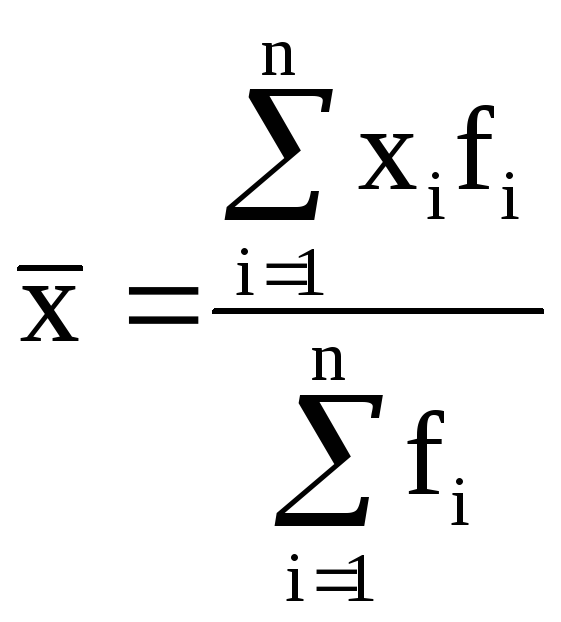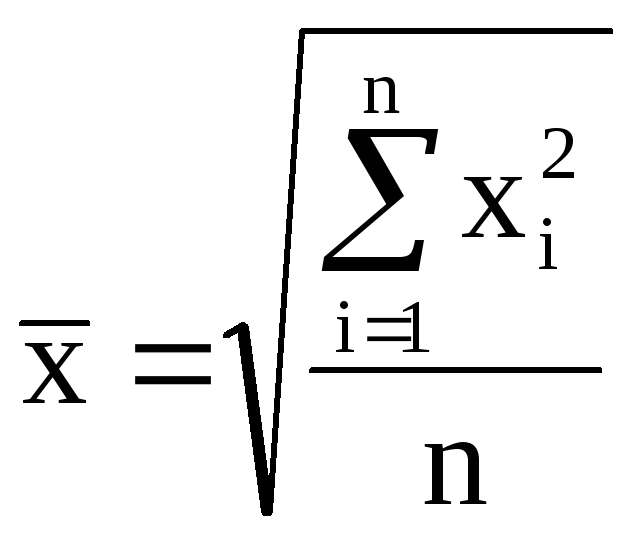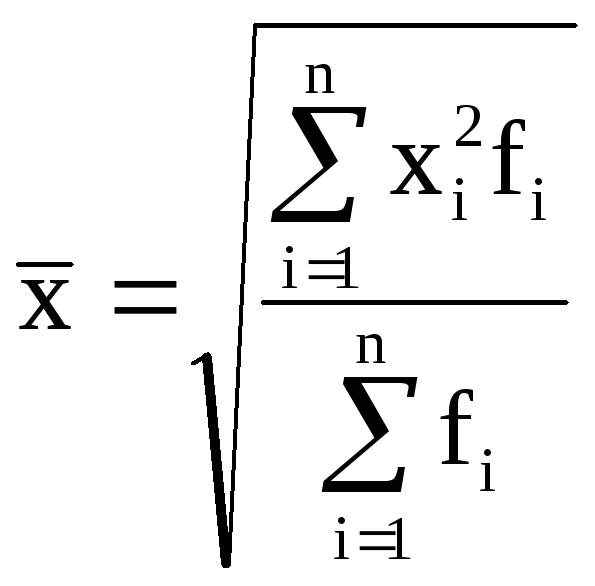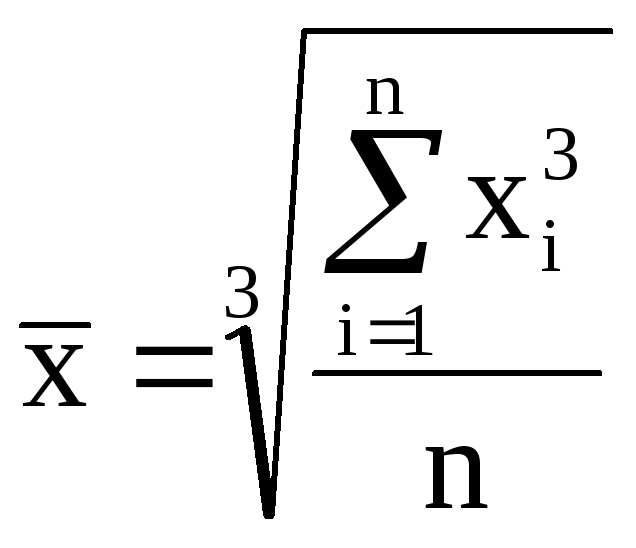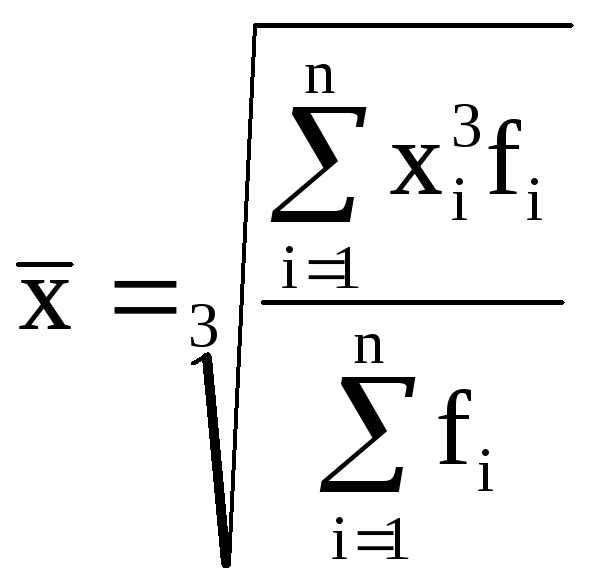
Рис. 1. 1. Структура статистической науки
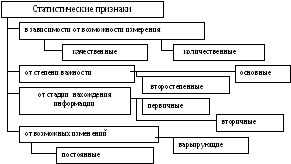
Рис. 1.2. Классификация статистических признаков

Рис. 3 .1. Классификация статистических сводок
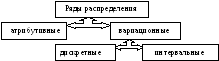
Р ис.
3.2. Ряды распределения
ис.
3.2. Ряды распределения
Рис. 4.1. Классификация статистических таблиц
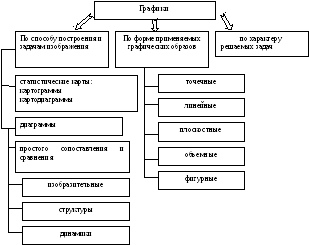
Рис. 4.3. Классификация графиков
Группировки. Абсолютные, относительные и средние показатели
Определение числа групп можно осуществить с помощью формулы Стерджесса
n = 1 + 3,322 lg N, (3.1)
где n – число групп; N – число единиц совокупности.
Величина равного интервала определяются по следующей формуле:
![]() (3.2)
(3.2)
где xmax, xmin – максимальное и минимальное значения признака в совокупности; n – число групп.
абсолютные статистические показатели выражаются чаще всего в следующих единицах измерения:
натуральных; стоимостных; трудовых; временных; подсчетом единиц совокупности.
Относительные показатели могут выражаться в
-
коэффициентах – если за базу сравнения принимается 1,
-
процентах (
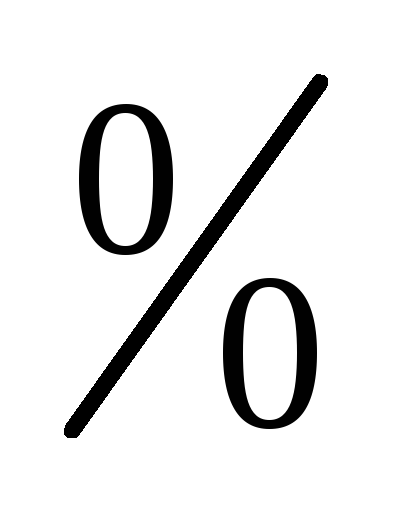 )
– если за базу сравнения принимается
100,
)
– если за базу сравнения принимается
100,
-
промилле (
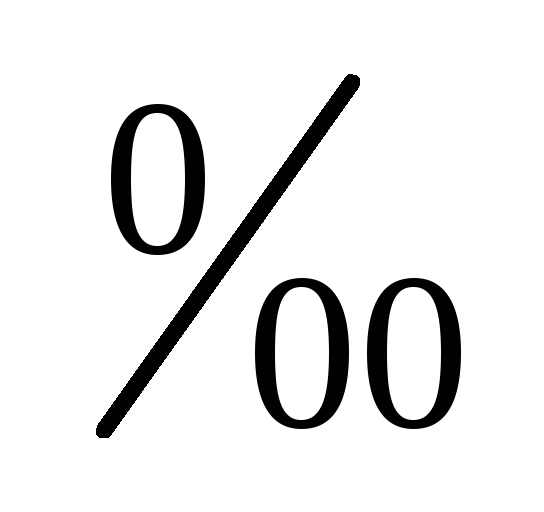 )
– если за базу сравнения принимается
1000,
)
– если за базу сравнения принимается
1000, -
продецимилле (
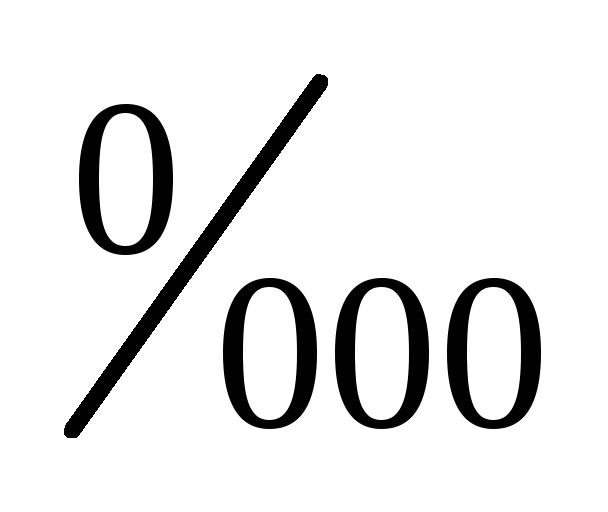 )
– если за базу сравнения принимается
10000.
)
– если за базу сравнения принимается
10000.
Относительная величина динамики (ОВД)
ОВД
=![]() 100
%,
(5.1)
100
%,
(5.1)
Относительная величина договорных обязательств (планового задания) (ОВДО)
ОВДО
=![]() 100
%,
(5.2)
100
%,
(5.2)
Относительная величина выполнения договорных обязательств (ОВВДО)
ОВВДО =![]() 100
%, (5.3)
100
%, (5.3)
ОВД
= ОВВДО
![]() ОВДО,
(5.4)
ОВДО,
(5.4)
т.е.
![]() =
=![]() .
(5.5)
.
(5.5)
Относительные величины структуры (ОВС)
ОВС,
%=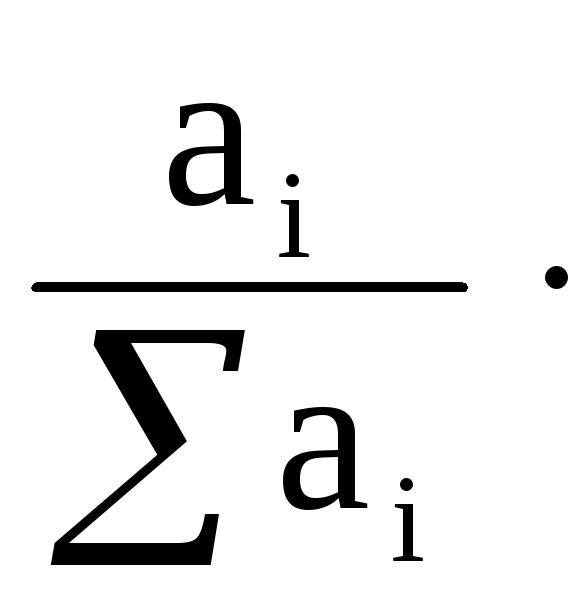 100
%,
(5.6)
100
%,
(5.6)
где
аi
– величина
изучаемой части совокупности;
![]() -
величина всей совокупности.
-
величина всей совокупности.
Относительные величины координации (ОВК)
ОВК
=
![]() ,
(5.7)
,
(5.7)
где ai – сравниваемая часть совокупности, bi– часть, принимаемая за основание или базу сравнения.
Относительная величина сравнения (ОВСр)
ОВСр
=
![]() .
(5.8)
.
(5.8)
Относительные величины интенсивности (ОВИ)
ОВИ
=![]() ,
(5.9)
,
(5.9)
где aA – показатель, характеризующий явление А,
BA – показатель, характеризующий среду распространения явления А.
Общий вид степенной средней (х):
![]() ,
,
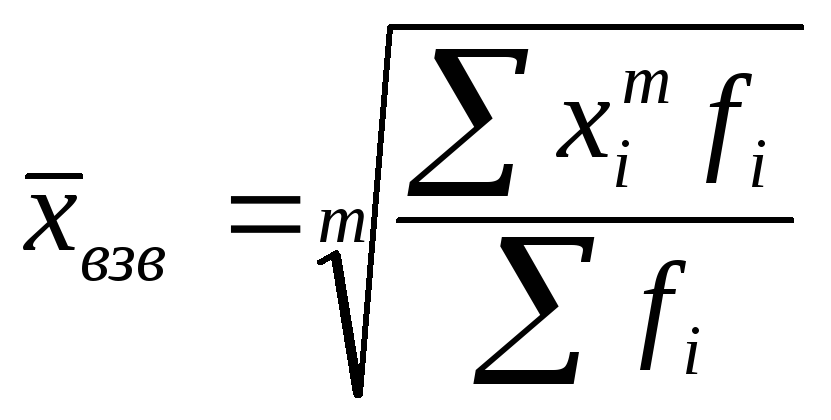 ,
(6.1)
,
(6.1)
где xi - варианта (значение) осредняемого признака;
m– показатель степени средней, определяющий ее вид; n – число вариант;
fi – частота, показывающая, сколько раз встречается i-е значение осредняемого признака.
Таблица 6.1 - Характеристики степенных средних
|
Вид степенной средней |
Показатель степени (m) |
Формулы расчета |
|
|
простая |
взвешенная |
||
|
г |
-1 |
|
|
|
г |
0 |
|
|
|
а |
1 |
|
|
|
квадратическая
|
2 |
|
|
|
кубическая |
3 |
|
|
1) Средняя арифметическая постоянной величины равна этой постоянной:
![]() при
при
![]() (6.4)
(6.4)
2) Общий множитель индивидуальных значений признака может быть вынесен за знак средней:
![]() (6.5)
(6.5)
3) Средняя суммы (разности) двух или нескольких величин равна сумме (разности) их средних:
![]() (6.6)
(6.6)
4) Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:
![]() (6.7)
(6.7)
5) Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю (нулевое свойство):
![]() (6.8)
(6.8)
6)Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на ту же величину:
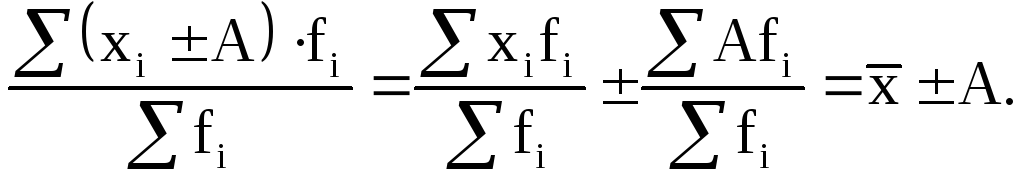 (6.9)
(6.9)
7) Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз:
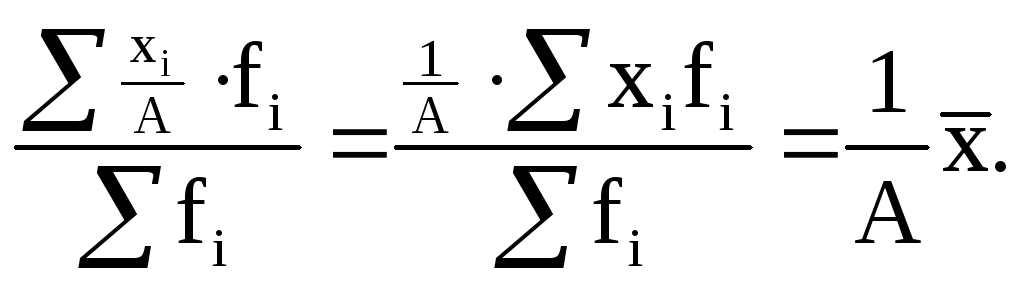 (6.10)
(6.10)
9) Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится:
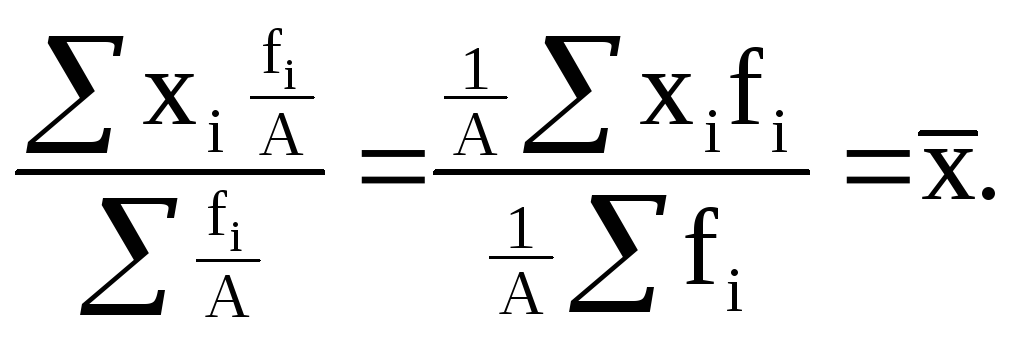 (6.11)
(6.11)
Медиана лежит в середине ранжированного ряда и делит его пополам.
Ряд, в котором значения признака располагаются в порядке возрастания или убывания, называется ранжированным.
![]() .
(6.15)
.
(6.15)
Этот номер соответствует медианному значению хМе для ранжированного ряда с нечетным числом членов.
Ме
=
![]() . (6.16)
. (6.16)
Медиана делит численность ряда пополам, следовательно, она там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности.
Формула медианы в интервальном ряду
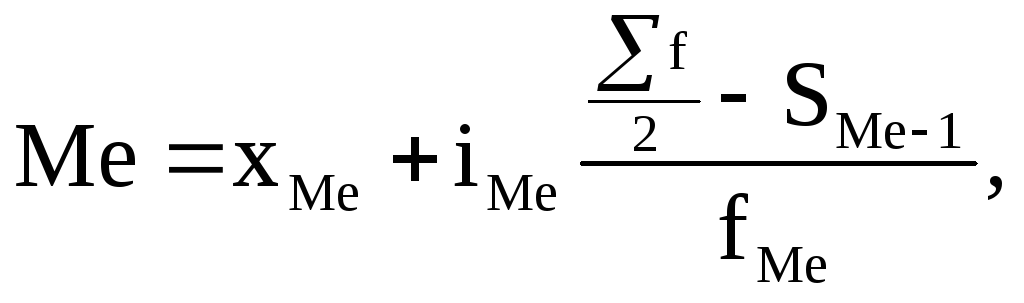 (6.17)
(6.17)
где хМе – нижняя граница медианного интервала;
iМе – величина медианного интервала;
![]() - полусумма частот
ряда;
- полусумма частот
ряда;
SМе-1 – сумма накопленных частот, предшествующих медианному интервалу;
fМе – частота медианного интервала.
Мода – наиболее часто встречающееся значение признака у единиц данной совокупности. Она соответствует определенному значению признака. В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном вариационном ряду модой приближенно считают центральный вариант так называемого модального интервала, т.е. того интервала, который имеет наибольшую частоту (частость). Значение моды для интервального ряда определяется формулой
![]() (6.18)
(6.18)
где хМо – нижняя граница модального интервала; iМо – величина модального интервала;
fМо – частота, соответствующая модальному интервалу; fМо-1 – частота, предшествующая модальному интервалу; fМо+1 – частота интервала, следующего за модальным.

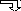 армоническая
армоническая
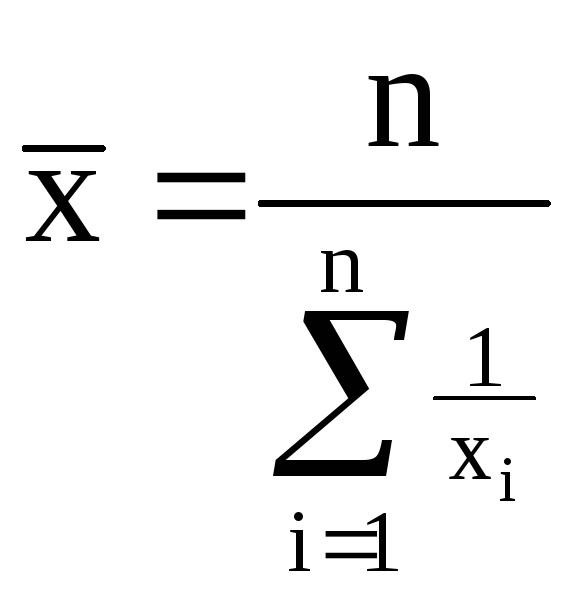
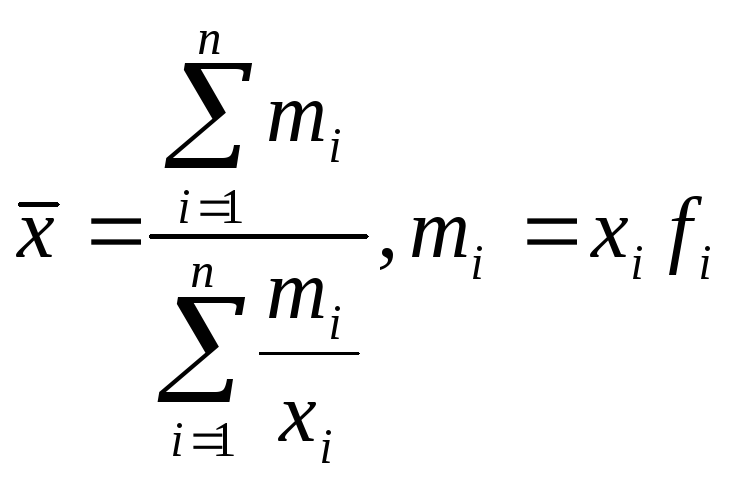
 еометрическая
еометрическая
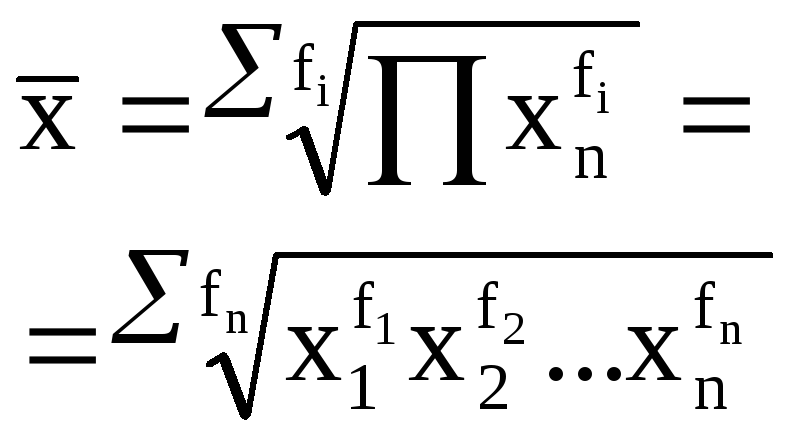
 рифметическая
рифметическая