2.2.3. Метод вариации произвольных постоянных

Если правая часть уравнения L(y)=f(x) не принадлежит ни к одному из рассмотренных в таблице 2 типов, то следует применять метод вариации произвольных постоянных. Рассмотрим его реализацию для дифференциальных уравнений второго порядка:

(2.40)

Сначала находится общее решение  соответствующего линейного однородного уравнения 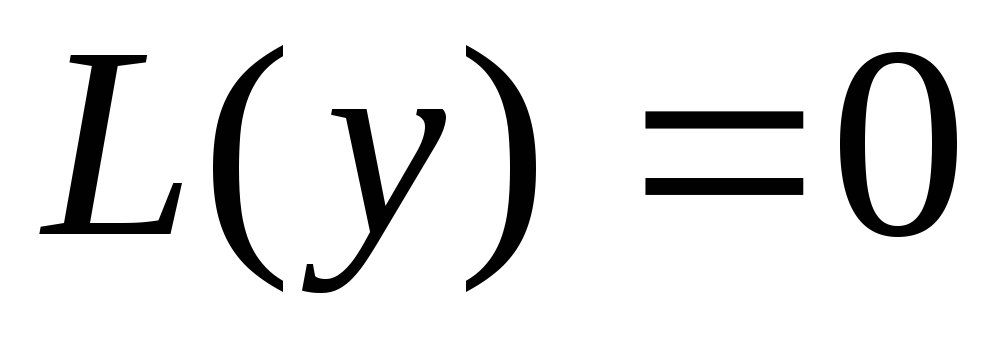в виде

(2.41)

где и- произвольные постоянные,- частные линейно независимые решения однородного уравнения.

Далее ищется решение неоднородного уравнения (2.40), по структуре, аналогичное (2.41), но произвольные постоянные в (2.41) заменяются неизвестными функциями, а именно принимается

(2.42)

Подстановка (2.42) в (2.40) приводит к следующей системе дифференциальных уравнений

(2.43)

в которой первое уравнение вводится произвольно. Определитель этой системы - определитель Вронского

так как функции илинейно независимы. Поэтому система (2.43), рассматриваемая как система линейных алгебраических уравнений относительно, имеет решение и притом единственное. Оно представляется в виде

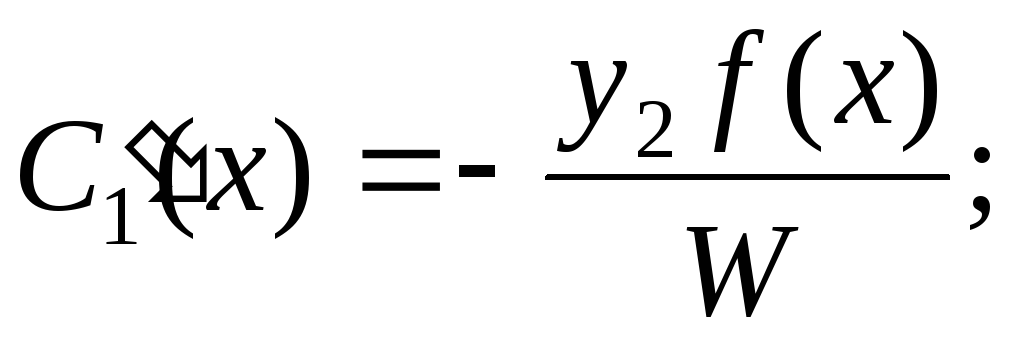
(2.44)

Интегрируя дифференциальные уравнения первого порядка (2.44), находим

(2.45)

 

Подставляя (2.45) в (2.42), получим общее решение неоднородного уравнения в виде

 

(2.46)

 Пример. Решить уравнение

 

(2.47)

 

1). Находим общее решение соответствующего однородного уравнения

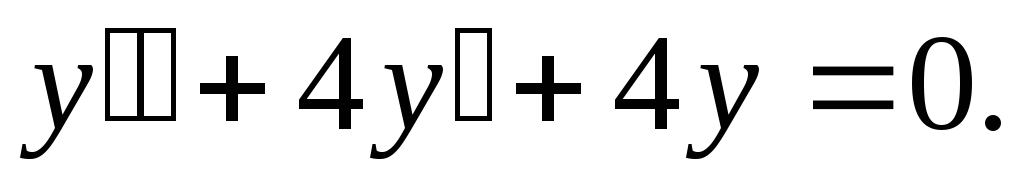
Составляем характеристическое уравнение Его корниСледовательно, частные линейно независимые решения равны ( см. таблицу 1, случай 3а )

а общее решение

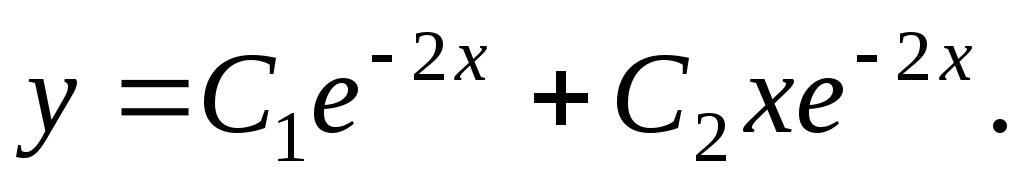
2). Так как правая часть неоднородного уравнения (2.47) не относится ни к одному из рассмотренных в таблице 2 случаев, то частное решение находим методом вариации произвольных постоянных. Принимаем

(2.48)

Тогда имогут быть найдены из решения системы (2.43)

Определитель этой системы

 

Поэтому выражения (2.44) принимают вид

(2.49)

Интегрируя уравнения (2.49), получим

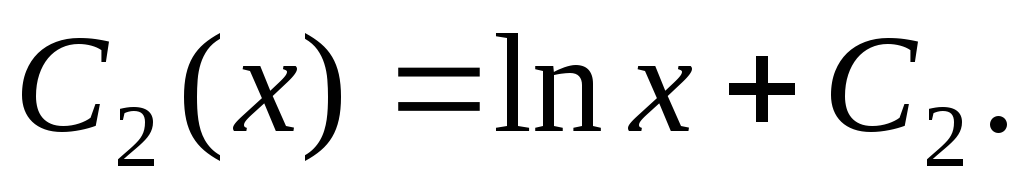(2.50)

Подставляя (2.50) в (2.48), находим общее решение уравнения в виде