2.2.2. Метод подбора частного решения

Этот метод не является универсальным и применим, если правая часть уравнения (2.28) в общем случае имеет вид

 

(2.34)

где P(x) и Q(x) - одночлены или многочлены (в общем случае различных степеней от x). Пусть при этом n - наивысшая степень одного из многочленов P(x) или Q(x).

Алгоритм построения частного решения неоднородного линейного дифференциального уравнения (2.28) следующий:

1. Находим корни характеристического уравнения (2.33).

2. Сравниваем конкретно заданную правую часть уравнения (2.28) с общим выражением (2.34), при котором применим метод подбора, и находим из этого сопоставления три числа:

3. Сравниваем "контрольное" комплексное число

с корнями характеристического уравнения и находим число m корней, совпавших с комплексным числом (если таких корней нет, то m=0).

4. Принимаем частное решение неоднородного уравнения (2.28)в виде

 

 (2.35)

где -многочлены одной и той же n-ой степени, но с неопределенными и различными коэффициентами.

5. Записываем решение (2.35) в развернутой форме в зависимости от n. Так,

если то

если то

 

6. Подставляем в исходное уравнение (2.28) и получаем систему алгебраических уравнений относительно неопределенных коэффициентов A,B,C...

 Замечание 1. Если правая часть уравнения (2.28) имеет более простой вид, например, содержит произведение степенной функции на показательную

 

(в частности, возможны случаи n=0 или (и) или содержит только линейную комбинацию тригонометрических функций вида

где M и N - постоянные числа, то частные решения неоднородного уравнения следует искать в форме, указанной в таблице 2 (в нее для полноты включен также общий случай).

Таблица 2

Структура частного решения уравненияв зависимости от вида правой части

1	, где -многочлен n-ой степени от x	A. Если число не совпадает ни с одним из корней характеристического уравнения, то частное решение следует принимать в форме где - многочленn-ой степени с неопределенными коэффициентами. Б. Если (-корень кратностиm, то
2	где M и N –заданные постоянные числа	A. Если мнимое число не совпадает ни с одним из корней: ( частное решение в форме где А и В – неопределенные коэффициенты Б. Если (- корень кратностиm, то
3	где и могочлены в общем случае различных степеней	А. Если комплексное число не совпадает ни с одним из корней:, то частное решение следует принимать в форме где ,- многочленыn-ой степени одного из многочленов P(x) или Q(x), но с неопределенными и различными коэффициентами. Б. Если (- корень кратностиm, то

 Замечание 2. Правая часть уравнения может  содержать только функцию видаили функцию вида. Но частное решение методом подбора следует искать в полной форме, содержащей ии(см. таблицу 2).

Процедура подбора неопределенных коэффициентов показана на примерах.

 Пример. Решить уравнение

1). Решаем сначала соответствующее однородное уравнение

Составляем характеристическое уравнение, отыскивая частные решения уравнения в виде . Получаем

.

Корни этого уравнения - действительны и различны. Соответствующие им частные линейно независимые решения ( см. таблицу 1 ) Поэтому общее решение однородного уравнения запишется в виде

(2.36)

2). Находим частное решение заданного неоднородного уравнения методом подбора, так как правая часть - многочлен третьей степени относится к первому из указанных в таблице 2 случаев.

Сравнивая функцию с выражением,заключаем, чтоа

Сравниваем  с корнями характеристического уравнения. Так както, и частное решение принимаем в виде

(2.37)

где A,B,C,D - неопределенные коэффициенты.

Подставляем (2.37) в исходное уравнение и приравниваем коэффициенты при одинаковых степенях x в левой и правой частях получающегося равенства:

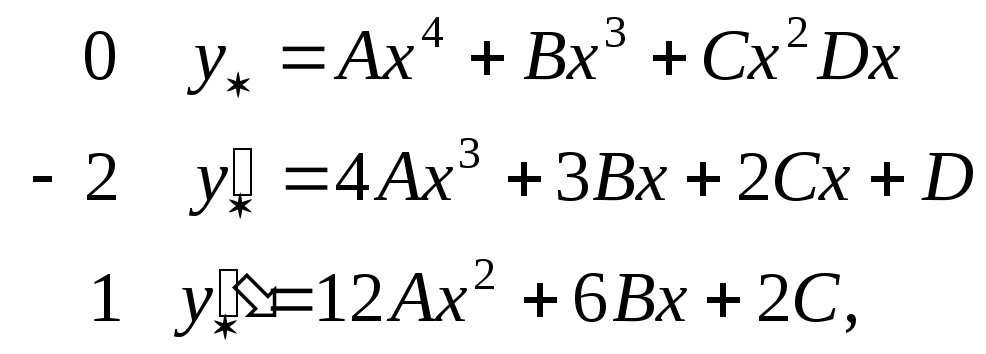
или

Решая систему алгеабраических уравнений находим коэффициенты: A=-1/8, B=-1/4, C=-3/8, D=1/2

Поэтому (2.38)

Складывая (2.36) и (2.38), получим общее решение уравнения в виде

 Пример. Решить уравнение

1). Общее решение однородного уравнения известно (2.36).

2). Находим частное решение неоднородного уравнения, сравнивая правую часть c выражением 2 из таблицы 2:

Получаем .

Сравниваем мнимое число с корнями характеристического уравнения. Так как(j=1,2 - номер корня), то.

Поэтому принимаем

где A и B - неопределенные коэффициенты.

Процедура вычислений имеет вид:

или

или

Приравнивая коэффициенты в обеих частях получившегося тригонометрического равенства при и, получим систему

откуда следует A = 3/8, В=-3.8.

 

Поэтому частное решение исходного уравнения будет

 

Общее решение запишется в виде

 Пример. Решить уравнение

1). Находим общее решение однородного уравнения

(2.39)

Характеристическое уравнение

имеет комплексные сопряженные кори: ,

Частные решения уравнения (2.39) будут (см. таблицу 1,случай 2a)

Поэтому 

2). Находим частное решение неоднородного уравнения. Сравниваем правую часть c общим выражением (1) из таблицы 2:

Видно, что в данном случае n=1, .

Так как (j=1,2), то m=0, поэтому принимаем ( см. табл.2, случай 2А ):

где A и B - неопределенные коэффициенты. Находим их, используя стандартную процедуру:

Сокращая на и приравнивая коэффициенты при одинаковых степенях x, получаем

откуда следует B=10/49.

Следовательно,

Окончательно имеем

 

 

 Пример. Решить уравнение

1). Однородное уравнение . Соответствующее ему характеристическое уравнениеимеет мнимые корни. Поэтому частные решения однородного уравнения будут (см. табл. 1, случай 2б ) . Общее решение примет вид

2). Находим сначала частное решение неоднородного уравнения

Сравниваемс выражением(см. табл.2, случай 2 ). ПолучаемТ=5. Сравниваемс корнямиТак как, тоПоэтому принимаемТогда

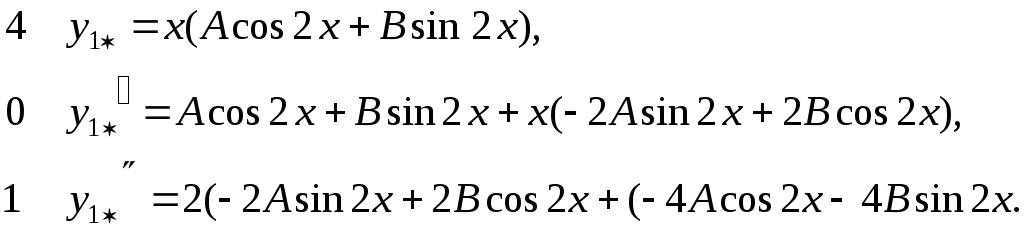
Приравнивая коэффициенты при sin 2x и cos 2x, получим A = -5/4,

B = 0. Следовательно,

3). Далее находим частное решение уравнения

При этом принимаем ( см. табл. 2, случай 2а )

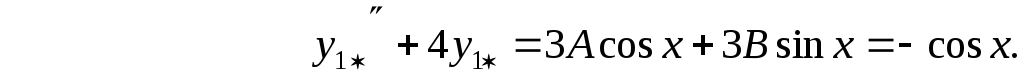
откуда следует Поэтому

Суммируя полученные решения, получим