15) Частные положения плоскостей в пространстве.

Рассмотрим изображение на эпюре и свойства плос­костей частного положения: плоскости, перпендикуляр­ные и параллельные плоскостям проекций.

Плоскости, перпендикулярные плоскостям проекций (проецирующие плоскости)

1. Горизонтально проецирующая плоскость a L я_х. Плоскость а, перпендикулярная горизонтальной плос­кости проекций я₁₍ называется горизонтально проеци­рующей (рис. 53, 54).

Основным свойством горизонтально проецирующей плоскости является то, что любая фигура, расположен­ная в этой плоскости, проецируется на я_х в прямую линию (горизонтальный след плоскости Л_0а, рис. 53, 54).

примеры изображения на эпюре горизонтально проецирующих плоскостей

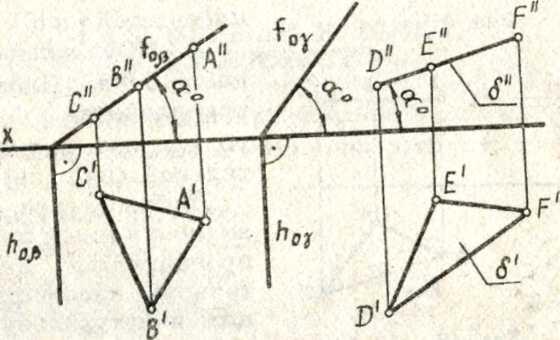
Основным свойством фронтально проецирую­щей плоскости является то, что любая фигура, рас­положенная в этой плос­кости, проецируется на тс₂ в прямую линию (фрон­тальный след плоскос­ти /о_Р, рис. 55, 56). Угол а⁰, который составляет фронтальный след шгос-Рис. 53 кости /₀р с координатной осью х, равен углу накло­на плоскости Р к плоскос­ти проекций 7tj. Горизон­тальный след такой плос­кости перпендикулярен

Плоскости, параллельные плоскостям проекций

1. Горизонтальная плоскость у j| тс,. Плоскость у, па-

раллельная плоскости тс_1; (рис. 57). называется горизонтальной

Любая фигура, распо­ложенная в такой плоскос­ти, проецируется на гори­зонтальную плоскость проекций в натуральную величину (А'В'С = ABC, рис. 57, 58). Фронтальный след этой плоскости па­раллелен оси х (/„у || х).

На рис. 58

показаны примеры изображения на эпюре горизонтальных плоскостей у и 5.

2. Фронтальная плос­кость 5 i тг₂. Плоскость 8, параллельная плоскос­ти л₂, называется фрон­тальной (рис. 59). .

Любая фигура, располо­женная в такой плоскости, проецируется на фрон­тальную плоскость проек­ций в натуральную вели­чину (А"В"С" = ABC, рис. 59, 60).

Горизонтальный след фронтальной плоскости параллелен оси х (h_№ \\ х).

На рис. 60 показаны примеры изображения на эпюре фронтальных плос­костей 5 и у.

Примечание. Плос­кость, параллельная одной из плоскостей проекций, является частным случаем проецирующих плоскос­тей.

Действительно, если плоскость у (рис. 57) па­раллельна горизонтальной плоскости проекций л,,, то она перпендикулярна дру­гой плоскости проекций (у L п₂) и является фрон­тально проецирующей. Любая плоская фигура, расположенная в такой плоскости, проецируется на одну плоскость проек­ций в натуральную вели­чину (А'В'С = ABC, рис. 57, 58; А"В"С = ABC, рис. 59, 60) и в прямую линию на другую плоскость проекций (А"В"С", рис. 57, 58; А'В'С, рис. 59, 60).

16) Прямая и точка в плоскости

Прямая АВ принадлежит плоскости а, если две ее точки А и В принадлежат этой плоскости а (справедливо и обратное: если точки А и В принадлежат плоскос­ти а, то прямая АВ, прохо­дящая через эти точки, принадлежит плоскос­ти сф

лежит плоской фигу­ре KLM, так как она проходит через точки А и В, расположенные на сторонах этой плоской фигуры. Прямая CD принадлежит плоскости, заданной парал­лельными прямыми с и d, так как она проходит через точки С и D, расположенные на этих прямых.

Прямая HF (рис. 62) принадлежит плоскости а, за­данной следами, так как она проходит через точки Н

и F, расположенные на следах этой плоскости h_Qa

Точки Н и F являются следами этой прямой, поэ­тому можно сделать вывод, что прямая при­надлежит плоскости, если ее следы принадлежат одновременно следам

плоскости (справедливо и обратное утверждение: если следы прямой при­надлежат следам плоскос­ти, то эта прямая принад­лежит плоскости):

Используя это свойст­во, можно перейти от лю­бого задания плоскости к заданию ее следами. На рис. 63 и 64 показано за­дание плоскости тремя точками А, В и С. Следы пря­мых АВ и СВ определяют положение горизонтально­го и фронтального следов

Точка К принадлежит плоскости а, если она рас­положена на прямой АВ, принадлежащей этой В»