12) Определение длины отрезка и углов наклона его к плоскостями проекций

На рис показаны в аксонометрической проекции отрезок АВ и его горизонтальная проекция А'В'. Про­ведя прямую ВВ_и параллельную горизонтальной про­екции отрезка А'В' (ВВ_Х \\ А'В'), получим прямоугольный треугольник ABB,.

Длина отрезка АВ равна гипотенузе этого треугольника, катетами которого являются гори­зонтальная проекция от­резка А'В' и разность коор­динат 2 точек

угол на­клона прямой к плоскости равен углу между этой прямой АВ и ее проек­цией на плоскость (А'В').

Следовательно, угол треугольника АВВ_и лежа­щий против катета Дг, равен углу наклона отрез­ка АВ к горизонтальной плоскости проекций тс_г

(угол а°).

Аналогично рассуждая , можно пока­зать, что длина отрез­ка АВ равна гипотенузе треугольника, катетами которого являются фрон­тальная проекция отрезка А"В" и разность коорди­нат у точек А и В (Дг/ = у_А - у_в)-

По аналогии длина от­резка АВ может быть оп­ределена и как гипотену­за треугольника, катеты которого — профильная проекция отрезка А"'В"' и разность координат.

На рис. 45 показан пример определения длины от­резка АВ и углов наклона его к плоскостям проекций (L_AB — длина отрезка АВ; а°, (3°, у° — углы наклона его соответственно к плоскостям проекций я_и я₂,

13) Метод конкурирующих точек.

Метод конкурирующих точек используется в на­чертательной геометрии для определения взаимной видимости двух геометри­ческих фигур.

Конкурирующими точ­ками называются такие точки пространства, у ко­торых совпадают какие-либо две одноименные проекции.

Метод конкурирующих точек заключается в опре­делении взаимной види­мости точек по их несо­впадающим проекциям. Так, точка В находится выше точки А относитель­но плоскости Я[ (г_в > г_л), поэтому на плоскости П1 видна точка В, которая закрывает точку А (счита­ется, что наблюдатель смотрит на плоскости про-

екций из бесконечности и направление луча зрения параллельно проецирующему лучу s).

На плоскости П2 видна точка D, так как она нахо­дится ближе к наблюдателю и закрывает невидимую точку С.

В дальнейшем методом конкурирующих точек будем пользоваться при определении видимости пересекаю­щихся геометрических фигур.

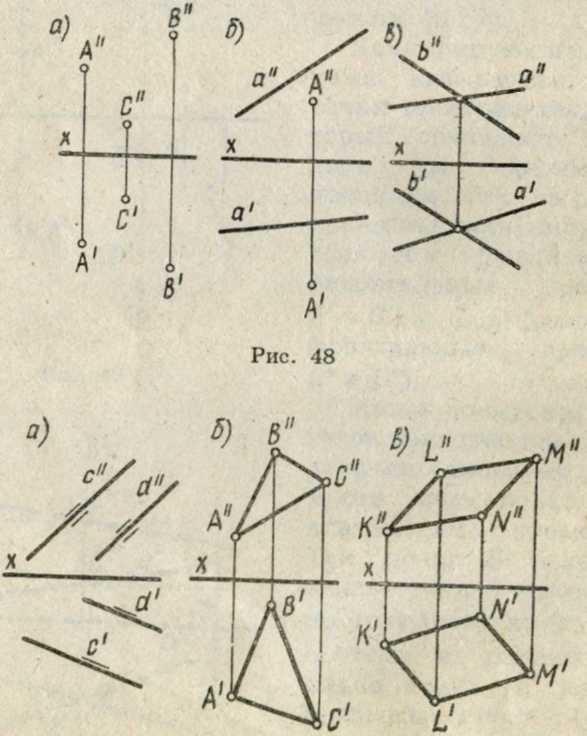
14) Способы задания плоскости

На эпюре плоскость может быть задана графически одним из следующих способов:

1) тремя точками, не лежащими на одной прямой (точки А, Б и С на рис. 48, а);

2) прямой и точкой вне ее (прямая а и точка А на рис. 48, б);

3) двумя пересека­ющимися прямыми (прямые а и Ь на рис. 48, в);

4) двумя парал­лельными прямыми (прямые с и d на рис. 49, а);

5) плоской фигурой (треугольник ABC и па­раллелограмм KLMN на рис. 49, б, в)',

(6) следами (рис. 50 и 51).

Следом плоскости а называется линия пе­ресечения этой плос­кости с плоскостью проекций имеет два следа (рис. 50 и 51

Для упрощения за­писи следы плоскости

могут обозначаться и так, как это показано на рис. 52 (плоскости р и у).

Точки пересечения плоскости а с координатными осями х, у и z называются точками схода следов и обозначаются соответственно Х_а, У_а и Z_a (рис. 50, 51 и 52).