5. Комплексные числа

Выражение вида , где и - вещественные числа, , называется комплексным числом (в алгебраической форме).

Комплексное число = называется комплексно-сопряженным числом к комплексному числу .

Действия над комплексными числами. Пусть даны два комплексных числа: и . Тогда

1)

2)

3) =.

Для любого комплексного числа имеем:

Величина называется модулем комплексного числа. Угол , определяемый равенствами , , называется аргументом комплексного числа.

Любое комплексное число можно записать в тригонометрической форме:

,

где .

Для выполнения действий возведения комплексного числа в натуральную степень и извлечения корня с натуральным показателем используются формулы Муавра:

1) ;

2) , .

Задание 5 Дано комплексное число . Требуется:

1. записать данное число в алгебраической и тригонометрической формах;

2. найти все корни уравнения .

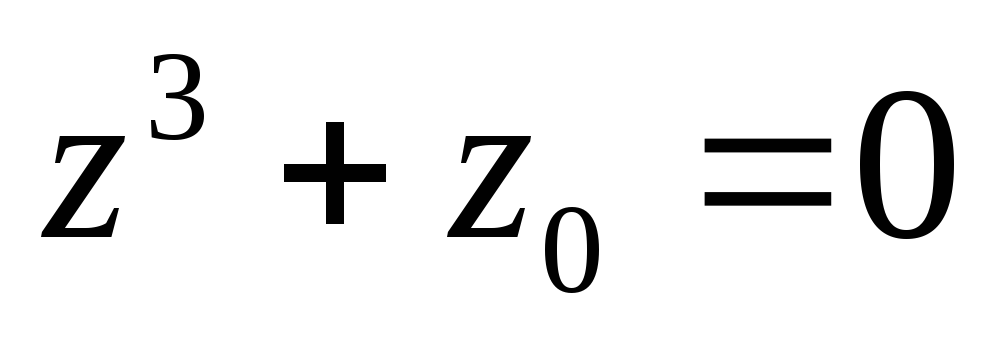Решение 1) Приведем комплексное число к алгебраической форме:.

Для этого умножим числитель и знаменатель дроби на число, комплексно-сопряженное знаменателю. Получим:

.

Это и есть алгебраическая форма комплексного числа , где .

Теперь приведем комплексное число к тригонометрическому виду: , где - модуль комплексного числа , - аргумент этого числа.

Для этого найдем . Для нахождения имеем систему:

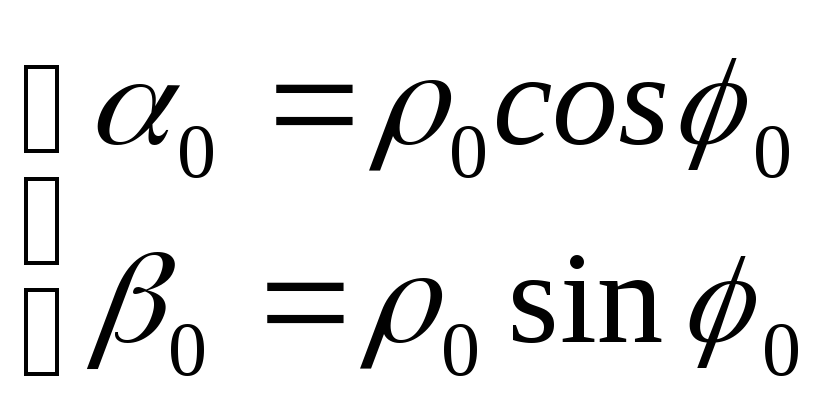
или

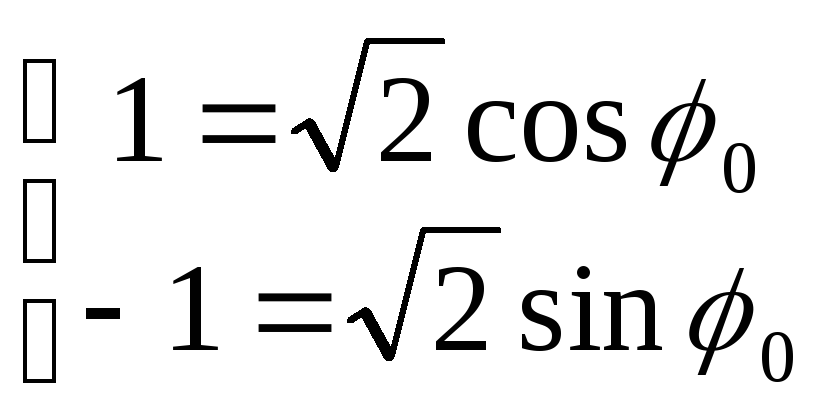
и тогда . Следовательно, тригонометрическая форма комплексного числа имеет вид:

.

3. Найдем теперь все корни уравнения , откуда Тригонометрическая форма комплексного числа - имеет вид: .

По второй из формул Муавра получаем:

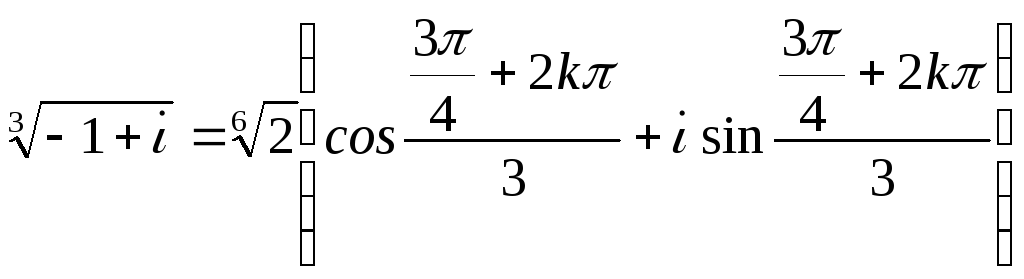, где

Тогда корни уравнения имеют вид:

1. При ;

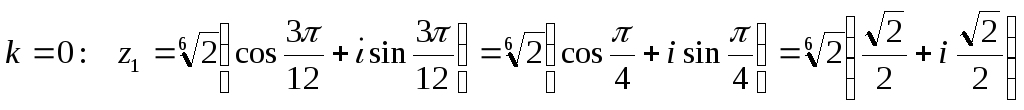2. При ;

3. При .

Глава 3. Введение в анализ. Дифференциальное исчисление функции одной переменной.

Теоретические вопросы

1. Понятие функции одной переменной.

2. Предел функции.

3. Непрерывность функции.

4. Бесконечно малые функции и их свойства.

5. Бесконечно большие функции и их свойства.

6. Односторонние пределы.

7. Производная функции.

8. Таблица производных.

9. Правила дифференцирования.

10. Производная сложной функции.

11. Производные высших порядков. Правило Лопиталя.

12. Исследование функций с помощью производных.

Литература

1. Н.С. Пискунов Дифференциальное и интегральное исчисления для втузов.- М.:Наука,1989,т.1,2.

2. В.С. Щипачев Высшая математика.- М.: Высшая школа, 1990.

3. П.Е. Данко, А.Г.Попов, Т.Я.Кожевникова Высшая математика в упражнениях и задачах.- М.: Высшая школа,1998,ч.1,2.

1. Предел функции

Пусть функция определена на множестве . Число А называется пределом функции при , если , что при .

Это записывают так:

.

Если и , то используют запись ; если и , то .

Числа и называются соответственно левосторонним и правосторонним пределами функции в точке .

Если существуют пределы и , то:

1) , где ;

2) ;

3) .

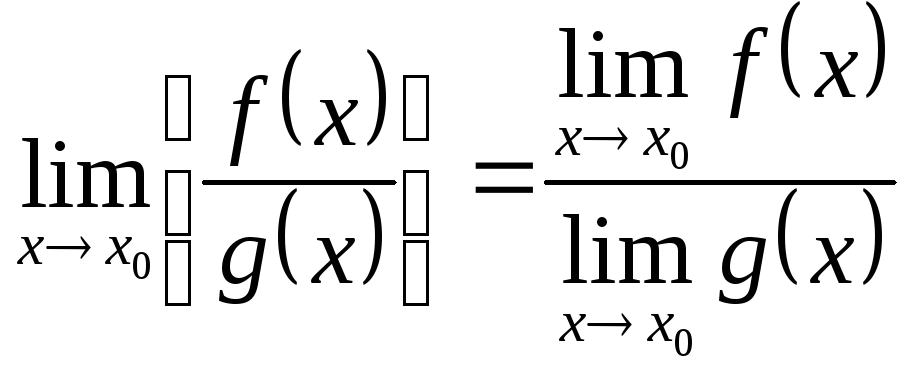
При решении задач полезно знать следующие “замечательные” пределы:

1) 2) ; 3) ; 4)

5)

Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводит к неопределенностям вида ,,,, и т.д.

Существуют различные приемы раскрытия данных неопределенностей:

деление числителя и знаменателя на старшую степень переменной (при ); сокращение на множитель, создающий неопределенность; применение “замечательных” пределов и т.п.

Задание 1. Найти пределы функций, не пользуясь правилом Лопиталя.

1)

Решение. При получаем неопределенность вида . Чтобы найти предел данной дробно - рациональной функции, необходимо предварительно разделить числитель и знаменатель дроби на , т.к. степень - наивысшая степень многочленов, определяющих данную рациональную функцию. Применяя основные теоремы о пределах и свойства бесконечно малых величин, получаем:

2)

Решение. Непосредственная подстановка предельного значения аргумента приводит к неопределенности вида . Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму

3)

Решение Здесь имеет место неопределенность вида . Вычисление данного предела основано на применении первого “ замечательного” предела ().Имеем:

4)

Решение. При данная функция представляет собой степень, основание которой стремится к 1, а показатель – к (неопределенность вида ). Преобразуем функцию так, чтобы использовать второй “замечательный” предел (). Получим:

.

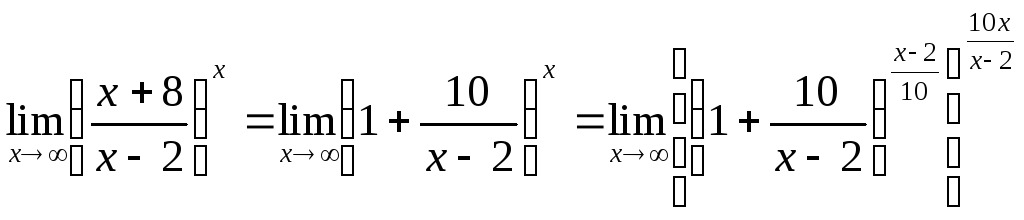Так как при ,то . Учитывая, что , находим .