
- •18. Гипербола: вывод уравнения, исследование формы, директрисы и асимптоты гиперболы.
- •17. Эллипс: вывод уравнения, исследование формы, параметры эллипса, его директрисы.
- •16. Окружность.
- •15.Прямая в r2. Различные виды уравнений прямой. Угол между двумя прямыми. Условия перпендикулярности, параллельности. Расстояние от точки до прямой.
- •13. Смешанное произведение векторов, свойства, выражение через координаты перемножаемых векторов.
- •12. Векторное произведение векторов, свойства, выражение через координаты перемножаемых векторов.
- •11. Скалярное произведение векторов, свойства, выражение через координаты перемножаемых векторов.
- •10.Векторы на плоскости и в пространстве. Линейные операции. Линейная зависимость и независимость векторов. Базис. Разложение вектора по базису в r2 и r3.
13. Смешанное произведение векторов, свойства, выражение через координаты перемножаемых векторов.
Определение.
Смешанным
произведением
векторов
![]() ,
,
![]() и
и
![]() называется число, равное скалярному
произведению вектора
называется число, равное скалярному
произведению вектора
![]() на вектор, равный векторному произведению
векторов
на вектор, равный векторному произведению
векторов
![]() и
и
![]() . Обозначается
. Обозначается
![]() или
(
или
(![]() ,
,
![]() ,
,![]() ).
).
Смешанное
произведение
![]() по
модулю равно объему параллелепипеда,
построенного на векторах
по
модулю равно объему параллелепипеда,
построенного на векторах
![]() ,
,
![]() и
и
![]() .
.
Свойства смешанного произведения:
1)Смешанное произведение равно нулю, если:
а)хоть один из векторов равен нулю;
б)два из векторов коллинеарны;
в)векторы компланарны.
2)![]()
3)![]()
4)![]()
5)
Объем треугольной пирамиды, образованной
векторами
![]() ,
,
![]() и
и
![]() ,
равен
,
равен
![]()
6)Если
![]() ,
,
![]() ,
то
,
то
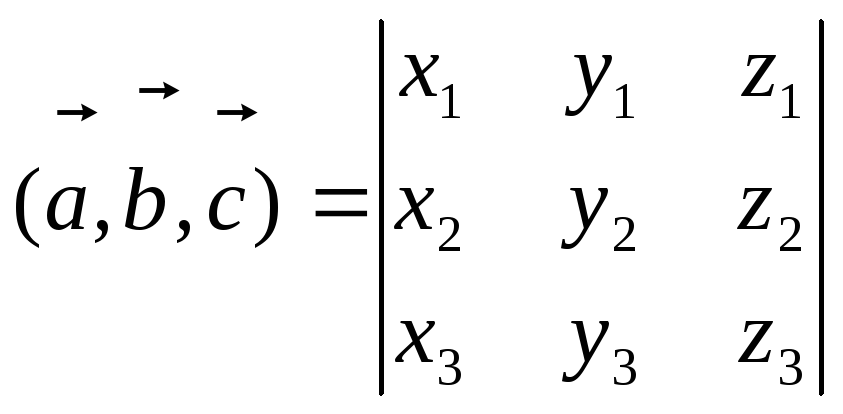
Пример. Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости.
Найдем
координаты векторов:
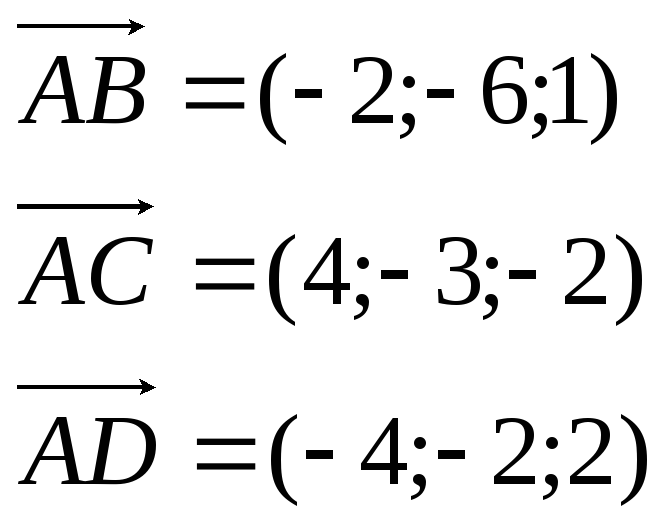
Найдем смешанное произведение полученных векторов:
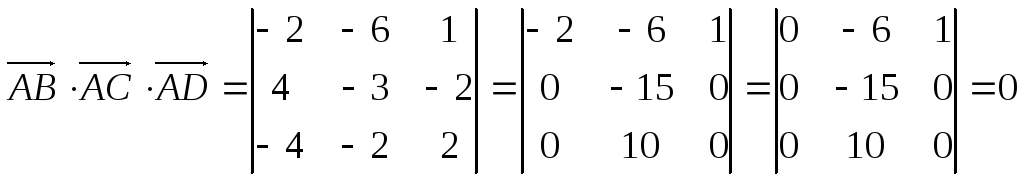 ,
,
Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости. Пример. Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2).
Найдем
координаты векторов:
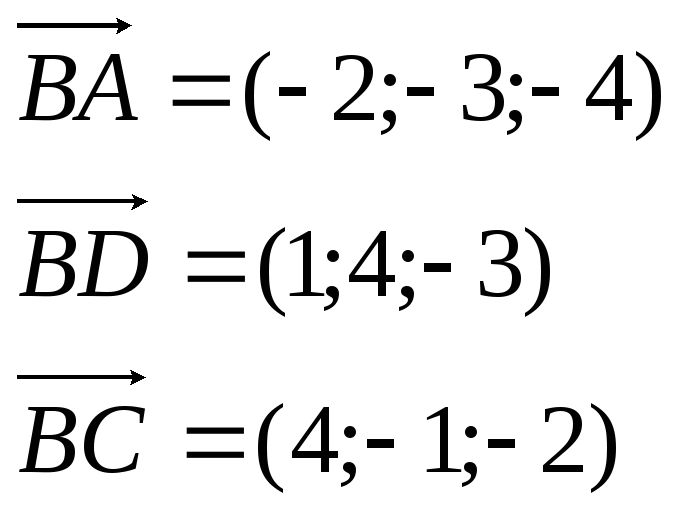
Объем
пирамиды
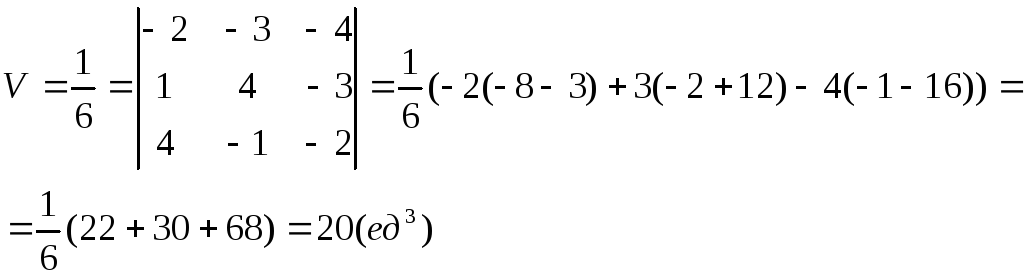
Для нахождения длины высоты пирамиды найдем сначала площадь основания BCD.
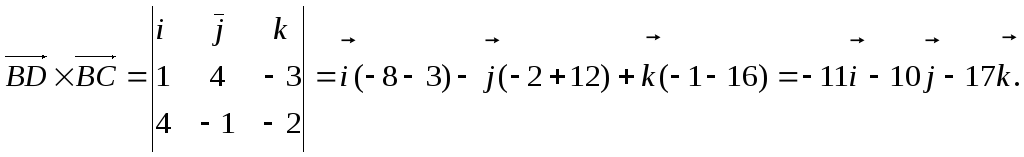
![]()
Sосн
=
![]() (ед2)
(ед2)
Т.к.
V
=
![]() ;
;
![]() (ед)
(ед)
12. Векторное произведение векторов, свойства, выражение через координаты перемножаемых векторов.
Определение.
Векторным
произведением векторов
![]() и
и
![]() называется вектор
называется вектор
![]() ,
удовлетворяющий следующим условиям:
,
удовлетворяющий следующим условиям:
1)
![]() ,
где
- угол между векторами
,
где
- угол между векторами
![]() и
и
![]() ,
,
![]()
2) вектор
![]() ортогонален
векторам
ортогонален
векторам
![]() и
и
![]()
3)
![]() ,
,
![]() и
и
![]() образуют правую тройку векторов.
образуют правую тройку векторов.
Обозначается:
![]() или
или![]() .
.
Свойства векторного произведения векторов:
1)
![]() ;
;
2)
![]() ,
если
,
если
![]()
![]() или
или
![]() =
0 или
=
0 или
![]() =
0;
=
0;
3)
(m![]() )
)![]() =
=
![]() (m
(m![]() )
= m(
)
= m(![]()
![]() );
);
4)
![]() (
(![]() +
+
![]() )
=
)
=
![]()
![]() +
+
![]()
![]() ;
;
5)
Если заданы векторы
![]() (xa,
ya,
za)
и
(xa,
ya,
za)
и
![]() (xb,
yb,
zb)
в декартовой прямоугольной системе
координат с единичными векторами
(xb,
yb,
zb)
в декартовой прямоугольной системе
координат с единичными векторами
![]() ,
то
,
то![]()
![]() =
=
-
Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах
 и
и
 .
.
Пример. Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3),
С(0, 1, 0).
![]()
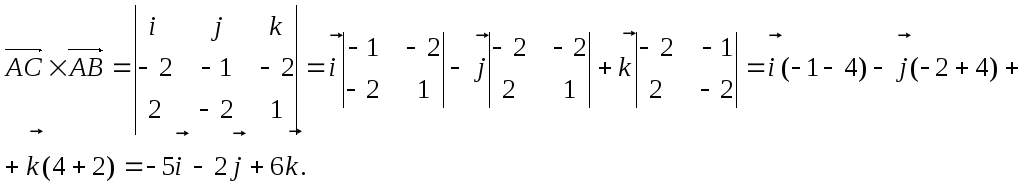
![]()
![]() (ед2).
(ед2).
Пример.
Доказать, что векторы
![]() ,
,
![]() и
и
![]() компланарны.
компланарны.
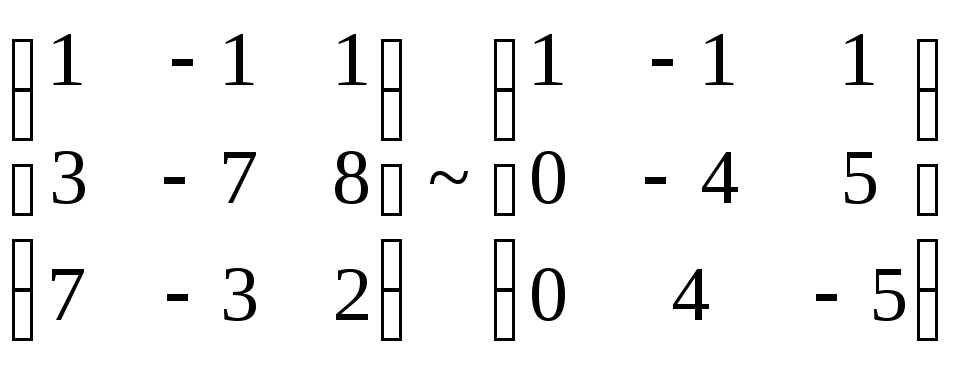 ,
т.к. векторы линейно зависимы, то они
компланарны.
,
т.к. векторы линейно зависимы, то они
компланарны.
Пример.
Найти площадь параллелограмма,
построенного на векторах
![]() ,
если
,
если
![]()
![]()
![]() (ед2).
(ед2).
11. Скалярное произведение векторов, свойства, выражение через координаты перемножаемых векторов.
Определение.
Скалярным произведением векторов
![]() и
и
![]() называется число, равное произведению
длин этих сторон на косинус угла между
ними.
называется число, равное произведению
длин этих сторон на косинус угла между
ними.
![]()
![]() =
= ![]()
![]() cos
cos
Свойства скалярного произведения:
-

 =
=  2;
2; -

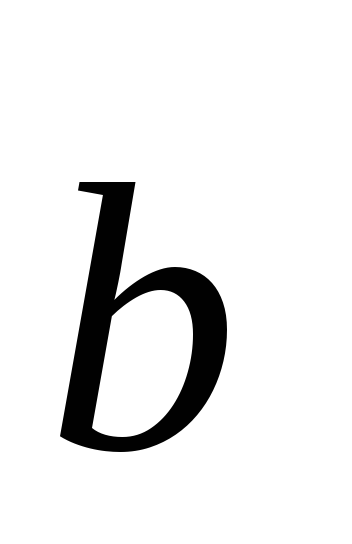 = 0, если
= 0, если

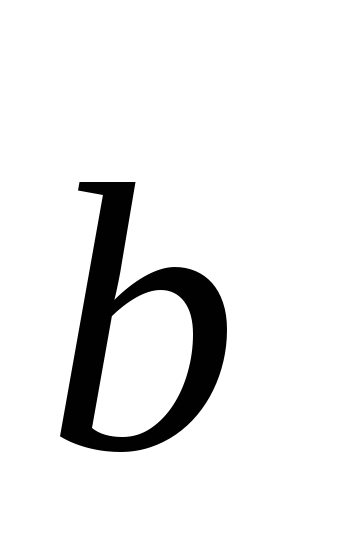 или
или
 =
0 или
=
0 или
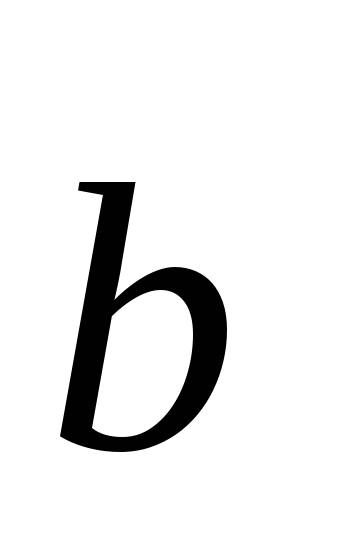 = 0.
= 0. -

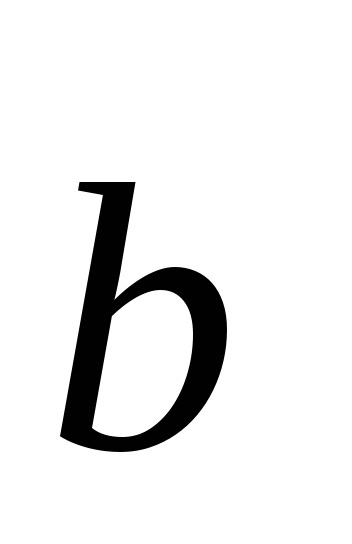 =
=

 ;
; -
 (
(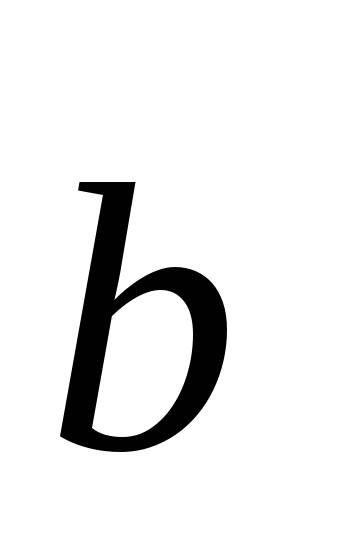 +
+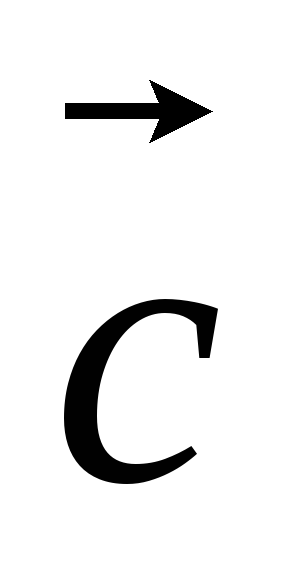 )
=
)
=

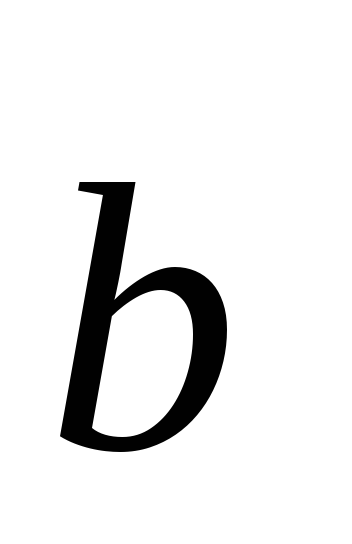 +
+

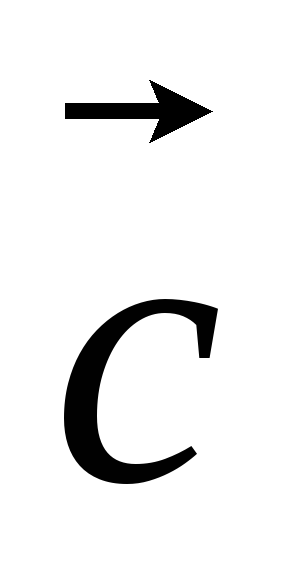 ;
; -
(m
 )
)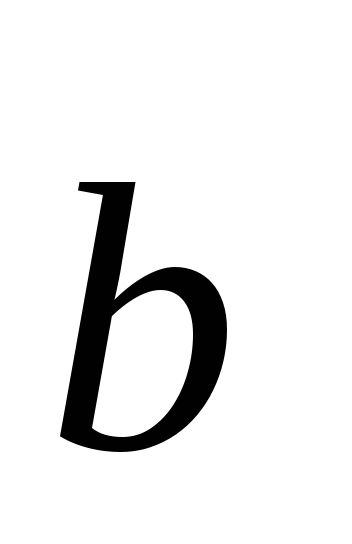 =
=
 (m
(m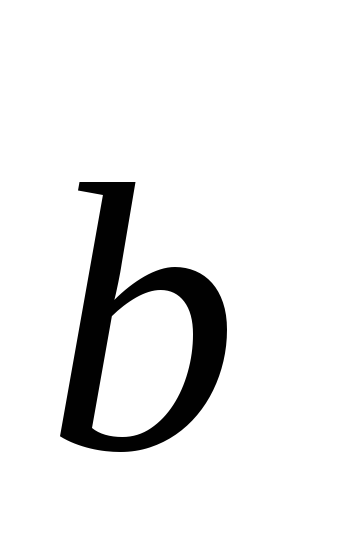 )
= m(
)
= m(
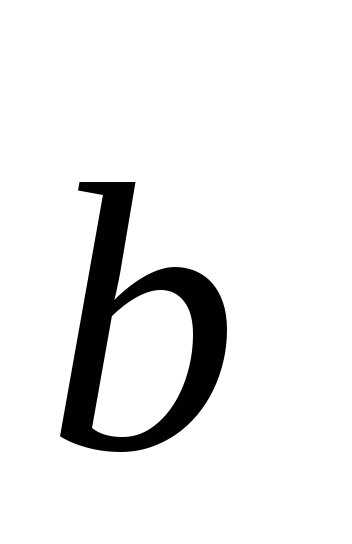 );
);
Если рассматривать
векторы
![]() в
декартовой прямоугольной системе
координат, то
в
декартовой прямоугольной системе
координат, то
![]()
![]() = xa
xb
+ ya
yb
+ za
zb;
= xa
xb
+ ya
yb
+ za
zb;
Используя полученные равенства, получаем формулу для вычисления угла между векторами:
![]() ;
;
Пример.
Найти векторное произведение векторов
![]() и
и
![]() .
.
![]() = (2, 5, 1);
= (2, 5, 1);
![]() =
(1, 2, -3)
=
(1, 2, -3)
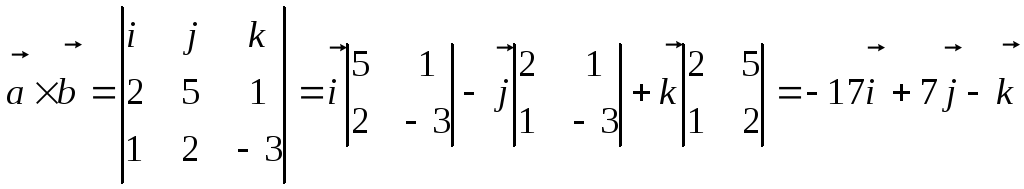 .
.
