Розв’язання

Дане рівняння визначає еліпсоїд у просторі. Знаходимо його найпростіше рівняння:

Відповідь: .

10.

З’ясувати геометричний зміст рівняння: x² = 2pz

Розв’язання

Дане рівняння на площині є рівнянням пароболи, симетричної відносно осі. У просторі – це рівняння є рівнянням параболічного циліндру, розташованого вздовж осі.

X

Z

X

Контрольна робота № 2

1. Обчислити вирази

1. ; 3. ; 5.

2. 4. ; 6. ; 10.

7. ; 8. ; 9.

2. Представити у вигляді многочлена першого степеня від тригонометричних функцій кутів, кратних х:

1. sin³x; 2. sin⁴x; 3. cos⁵x; 4.cos⁶x; 5. sin³x·cos⁵x;

6. 3sin⁴xcos³x; 7. 5cos³xsin²x; 8. sin⁷x; 9. cos⁴xsin³x; 10.sin⁵x.

3. Обчислити суми:

   1. cos x + cos 2x+ …+ cos nx; 5. cos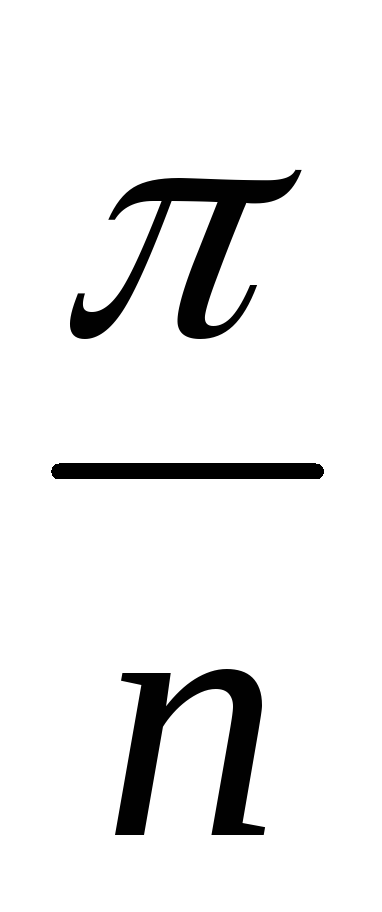+cos+cos+…+cos

   2. sin x + sin 2x + …+ sin nx; 6. sin+sin+sin+…+sin

   3. sin x + 2sin 2x + …+ nsin nx; 7. cos² x + cos² 2x+ …+ cos² nx;

   4. cos x +2cos 2x+ …+ ncos nx; 8. sin² x + sin² 2x + …+ sin² nx;

9. + cos x + cos 2x+ …+ cos nx; 10. 1+acosφ+a²cos2φ+…+a^kcoskφ.

4. 1. Знайти суму всіх коренів 6-го степеня з одиниці.

2. Довести, що первісний корінь n-го степеня з одиниці має порядок n.

3. Знайти суму всіх коренів 15-го степеня з одиниці.

4. Знайти суму всіх первісних коренів 10 степеня з одиниці.

5. Знайти суму всіх первісних коренів 15-го степеня з одиниці.

6. Знайти необхідну і достатню умови того, щоб кожен первісний корінь nm-го степеня з одиниці можна було зобразити у вигляді добутку первісних коренів n-го і m-го степенів з одиниці.

7. Знаючи, що є одним із значень , знайти всі значення .

8. Знаючи, що 2+і є одним із значень , знайти всі значення .

9. Знайти суму всіх коренів n-го степеня з одиниці.

10. Знайти суму всіх первісних коренів 24-го степеня з одиниці.

5. Дана система лінійних неоднорідних рівнянь:

(*)

1. Знайти ранг матриці А системи (*) А=.

2. Дослідити систему на сумісність.

3. Обчислити визначник матриці А способом:

а) зведенням до трикутного вигляду;

б) розкладанням за елементами першого рядка.

4. Розв'язати систему рівнянь методом Гауса, методом Крамера;

5. Знайти матрицю, обернену до матриці А системи двома способами:

а) за допомогою матриці А^*- приєднаної до матриці А:

б) за допомогою комбінованої матриці: (А/Е)~(Е/A^-1).

6) Записати систему (*) в матричному вигляді та розв’язати її в матричному вигляді.

Таблиця значень параметрів системи (*)

Варіант параметр	1	2	3	4	5	6	7	8	9	10
a	2	1	3	4	3	1	0	5	5	2
b	3	2	4	5	4	2	1	6	6	3
c	2	1	-4	-3	3	3	0	5	-5	-2
e	-2	3	5	-4	-2	-2	1	-4	6	3
f	2	1	1	1	3	4	0	5	-5	3
d	-1	-2	-2	1	0	1	-3	2	-8	-1

VI. За допомогою теореми про накладання розв’язків знайти загальний розв’язок системи лінійних рівнянь (*).

(*)

Таблиця значень параметрів системи (*)

Варіант параметр	1	2	3	4	5	6	7	8	9	10
m	7	6	5	6	4	5	3	5	1	8
n	-1	-3	0	2	-2	-5	1	5	-2	1