
- •С. Колеснік
- •Методичний посібник
- •Збірник контрольних робіт. Аналітична геометрія та лінійна
- •Контрольна робота № 1
- •Зразки розв’язання задач контрольної роботи №1
- •1) Довести, що з половини діагоналей будь-якого чотирикутника і будь-якої із його середніх ліній можна скласти трикутник.
- •2) Довести, що три висоти трикутника перетинаются в одній точці.
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Розв’язання
- •Контрольна робота № 2
- •Зразки розв’язання задач контрольної роботи №2
- •Контрольна робота № 3
- •1. Перевірити чи утворюють наступні множини векторні простори над полем дійсних чисел r
- •Зразки розв’язання задач контрольної роботи № 3
- •Розв’язання. Нехай м- множина всіх квадратних матриць порядку n з дійсними елементами. Покажемо, що м-абелева група відносно операції додавання.
- •Контрольна робота № 4
- •Зразки розв’язання задач контрольної роботи № 4 і. Для квадратичної форми f знайти:
- •Контрольна робота №5.
- •Зразки розв’язання задач контрольної роботи №5
- •Контрольна робота № 6
- •Зразки розв’язання задач контрольної роботи № 6
- •Контрольна робота №7
- •Зразки розв’язання задач контрольної роботи № 7
- •Контрольна робота № 8.
- •Зразки роз`язання задач контрольної роботи № 8
- •Для простого модуля старший коефіцієнт взаємнопростий з ним. Визначимо множник k так, щоб . Матимемо . Домножаючи обидві частини заданої конгруенції на 10 за модулем 13, дістаємо
- •Контрольна робота № 9
- •Зразки розв‘язання задач контрольної роботи № 9
- •Тоді з рівності
- •Додаток: таблиці первісних коренів та індексів
- •Література
- •Методичне видання Колеснік Світлана Григоровна
- •Методичний посібник
Контрольна робота № 8.
-
Розв`язати конгруенції:
-
 ,
, -
 (mod
5),
(mod
5), -
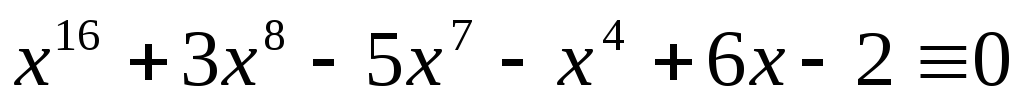 (mod
7),
(mod
7), -
 (mod
11),
(mod
11), -
 (mod
11),
(mod
11), -
 (mod
3),
(mod
3), -
 (mod
5),
(mod
5), -
 (mod
5),
(mod
5), -
 (mod
5),
(mod
5), -
 (mod
5).
(mod
5).
-
-
Розв`язати конгруенції, звівши їх до двочленних:
-
 (mod
5),
(mod
5), -
 (mod
17),
(mod
17), -
 (mod
31),
(mod
31), -
 (mod
41),
(mod
41), -
 (mod
47),
(mod
47), -
 (mod
13),
(mod
13), -
 (mod
23),
(mod
23), -
 (mod
5),
(mod
5), -
 (mod
7),
(mod
7), -
 (mod
7).
(mod
7).
-
-
Користуючись критерієм Ейлера знайти всі квадратні лишки за модулем:
-
5;
-
7;
-
11;
-
13:
-
17;
-
23;
-
37;
-
53;
-
19;
-
43.
-
-
Знайти порядок числа a за модулем m, якщо:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
a |
5 |
2 |
4 |
10 |
2 |
7 |
3 |
4 |
5 |
5 |
|
m |
13 |
5 |
5 |
13 |
17 |
43 |
7 |
7 |
7 |
11 |
-
Знайти всі первісні корені за модулем m:
|
варіант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
m |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
37 |
41 |
-
Розв`язати конгруенції:
-
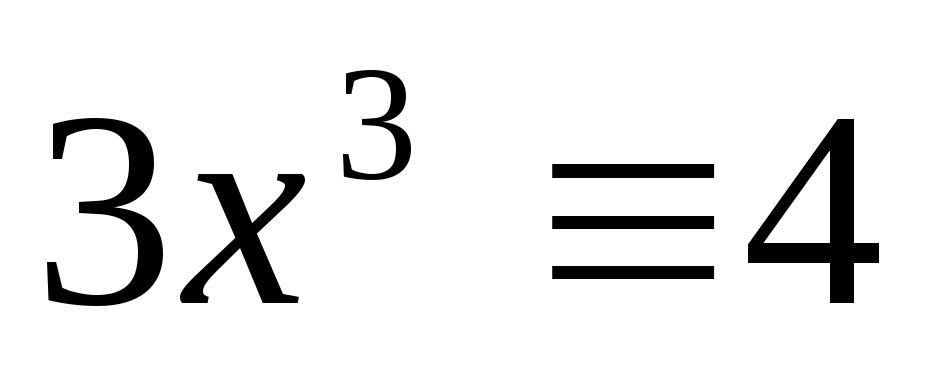 (mod
7),
(mod
7), -
 (mod
13),
(mod
13), -
 (mod
23),
(mod
23), -
 (mod
31),
(mod
31), -
 (mod
37),
(mod
37), -
 (mod
61),
(mod
61), -
 (mod
73),
(mod
73), -
 (mod
73),
(mod
73), -
 (mod
73),
(mod
73), -
 (mod
79).
(mod
79).
-
-
Знайти найменше натуральне число x, яке задовольняє наступній конгруенції:
-
 (mod
13),
(mod
13), -
 (mod
17),
(mod
17), -
 (mod
31),
(mod
31), -
 (mod
31),
(mod
31), -
 (mod
31),
(mod
31), -
 (mod
37),
(mod
37), -
 (mod
41),
(mod
41), -
 (mod
43),
(mod
43), -
 (mod
53),]
(mod
53),] -
 (mod
67).
(mod
67).
-
-
Знайти остачу від ділення;
-
 на
35;
на
35; -
 на
29;
на
29; -
 на
37;
на
37; -
 на
29;
на
29; -
 на
67;
на
67; -
 на
73;
на
73; -
 на
79;
на
79; -
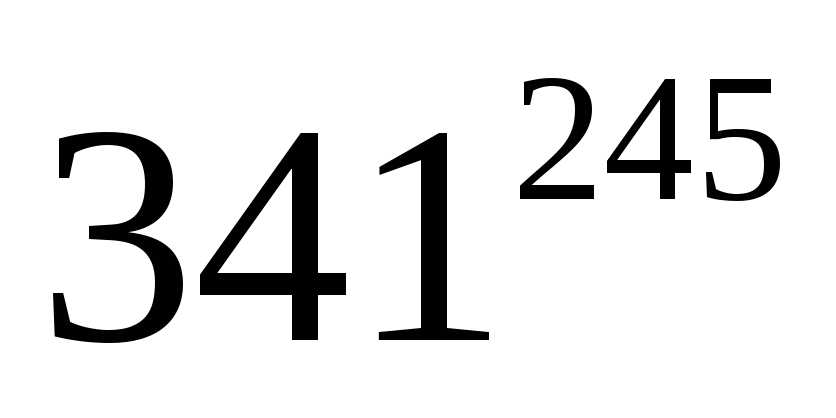 на
89;
на
89; -
 на
629;
на
629; -
 на
135.
на
135.
-
Зразки роз`язання задач контрольної роботи № 8
-
Розв`язати конгруенцію:
![]() (mod
5).
(mod
5).
Розв`язання.
Конгруенцію замінимо еквівалентною їй конгруенцією степеня не вище 4 за тим же самим модулем 5.
Поділимо
![]() на
на
![]() .
Дістанемо
.
Дістанемо
![]()
Замінивши
всі коефіцієнти остачі найменшими
лишками за модулем 5, дістанемо, що дана
конгруенція еквівалентна конгруенції
![]() (mod
5). (1)
(mod
5). (1)
Замінимо цю конгруенцію еквівалентною їй конгруенцією із старшим коефіцієнтом, що дорівнює 1. Розв`яжемо конгруенцію:
![]() (mod
5).
(mod
5).
Додамо до правої частини модуль:
![]() (mod
5).
(mod
5).
Обидві частини ділимо на 3:
![]() (mod
5).
(mod
5).
Домножимо конгруенцію (1) на 2:
![]() (mod
5).
(mod
5).
Останню конгруенцію замінимо еквівалентною їй:
![]() (mod
5).
(2)
(mod
5).
(2)
О скільки
скільки
![]() (mod
5),
то (x,
5)=1,
а тому
(mod
5),
то (x,
5)=1,
а тому
![]() (mod
5).
Тоді конгруенція (2) матиме вигляд
(mod
5).
Тоді конгруенція (2) матиме вигляд
![]() (mod
5).
(3)
(mod
5).
(3)
Оскільки (x, 5)=1, то обидві частини конгруенції (3) можна скоротити на x:
![]() (mod
5)
(4)
(mod
5)
(4)
Конгруенція (4) має такі розв`язки:
![]() (mod
5)
і
(mod
5)
і
![]() (mod 5).
(mod 5).
Отже, конгруенція (1) має розв`язки:
![]() 2;
3 (mod
5).
2;
3 (mod
5).
Зауваження:
Замість того, щоб ділити
![]() на
на
![]() ,
можна було б замінити
,
можна було б замінити
![]() на
на
![]() ,
де r
– остача від ділення s
на 5-1= 4, причому якщо s
ділиться на 4, то покладаємо r=4.
Тоді
,
де r
– остача від ділення s
на 5-1= 4, причому якщо s
ділиться на 4, то покладаємо r=4.
Тоді
![]() (mod
5);
(mod
5);
![]() ;
;
![]() ;
;
![]() .
.
Отже,
![]() .
.
-
Розв`язати конгруенцію, звівши її до двочленної:
 .
.
Розв`язання.
