Контрольна робота №7

Варіант 1.

1. Знайти усі натуральні числа n, для яких число n²+1 ділиться на n+1.

2. Довести, що сума квадратів двох непарний чисел не може бути квадратом цілого числа.

3. Знайти всі значення простого числа р, якщо 4p²+1 і 6p²+1 прості числа.

4. Знайти натуральні числа a і b, якщо (a,b)=24; [a,b]=2496.

5. Знайти кількість натуральних чисел, менших за число 1476 та маючих з ним НСД число 41.

6. Знайти остачу від ділення 109³⁴⁸ на 14.

7. Скількома нулями закінчується число n!, якщо n=50.

8. Розв’язати конгруенцію 20x 10(mod 25).

9. Розв’язати у цілих числах рівняння 45x-37y=25.

10. Скоротити дріб : .

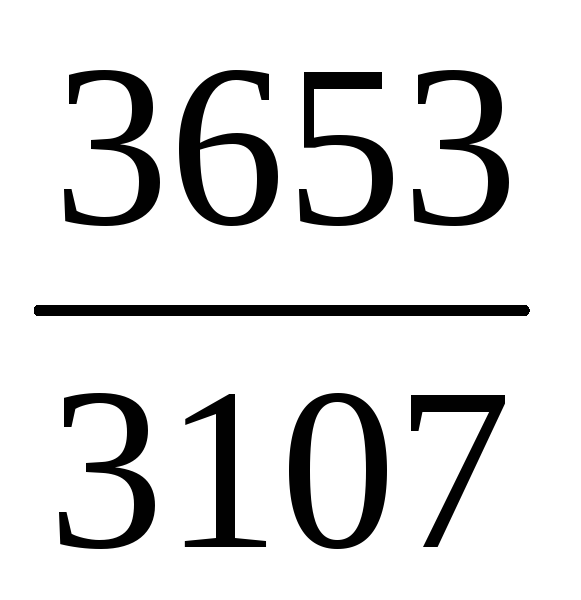11. Ірраціональне число 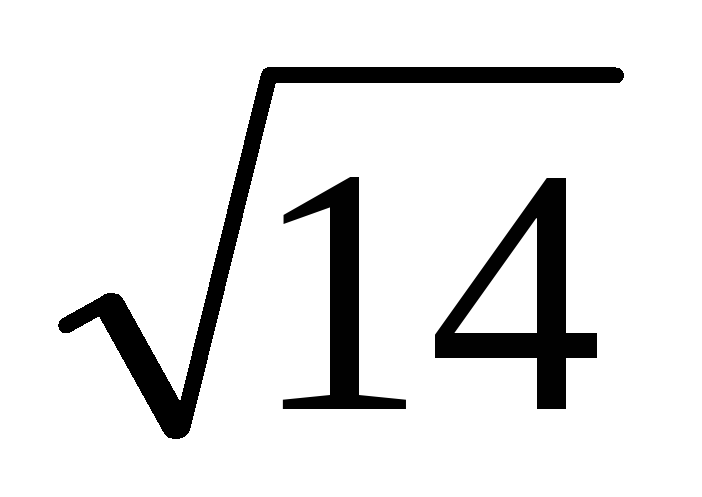розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення .

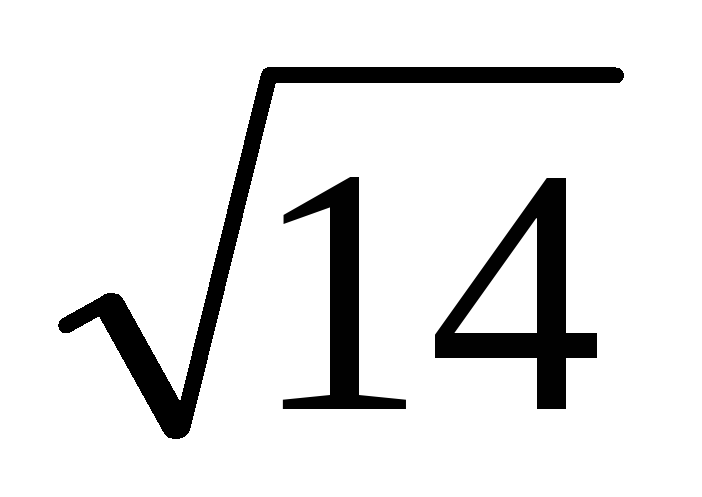Варіант 2.

1. Довести, що квадрат від непарного числа, відмінного від нуля, при діленні на 8 дає остачу 1.

2. Довести, що для кожного натурального числа n число 3(1⁵+2⁵+...+n⁵) ділиться на число (1³+2³+...+n³).

3. Знайти всі прості числа, які є одночасно сумами і різницями простих чисел.

4. Знайти натуральні числа a і b, якщо a+b=667; [a,b]=120(a,b).

5. Знайти кількість натуральних чисел, які менші від числа 300 і мають з ним НСД число 20.

6. Знайти остачу від ділення 439²⁹¹ на 60.

7. Скількома нулями закінчується число n!, якщо n=123.

8. Розв’язати конгруенцію 15x 3(mod 45).

9. Розв’язати у цілих числах рівняння 81x-48y=33.

10. Скоротити дріб : .

11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення .

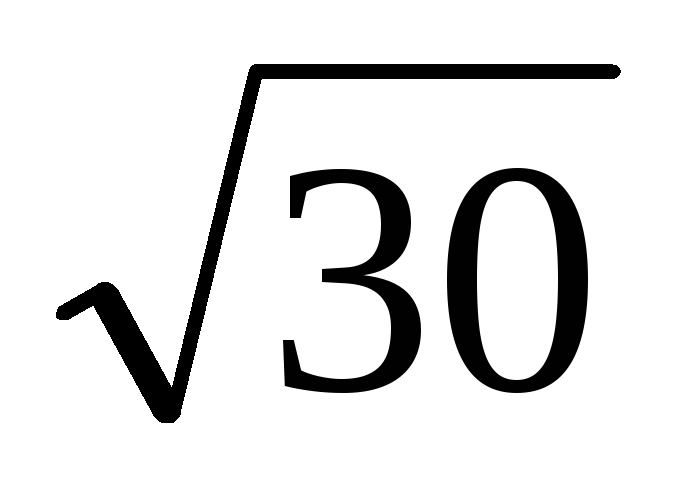Варіант 3.

1. Довести, що сума кубів трьох послідовних цілих чисел ділиться на 9.

2. Показати, що якщо mn+pq ділиться на m-p, то і mq+np ділиться на m-p, де m,n,p,q – цілі числа.

3. Знайти значення простого числа р, якщо відомо, що p+10 і p+14 - прості числа.

4. Знайти натуральні числа a і b, якщо a∙b=720; (a,b)=4.

5. Знайти кількість натуральних чисел, які менші від числа 1665 і мають з ним НСД число 37.

6. Знайти останні три цифри числа 243⁴⁰².

7. Знайти число N, добуток усіх дільників якого дорівнює 5832.

8. Розв’язати конгруенцію 78x 42(mod 51).

9. Розв’язати у цілих числах рівняння 17x-25y=117.

10. Скоротити дріб : .

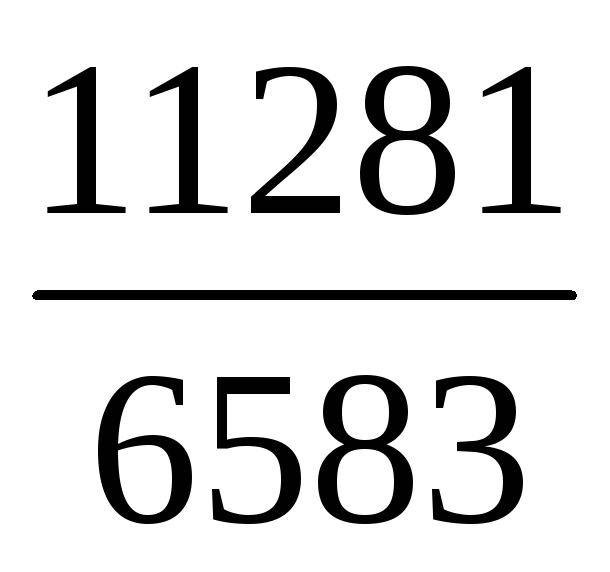11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення .

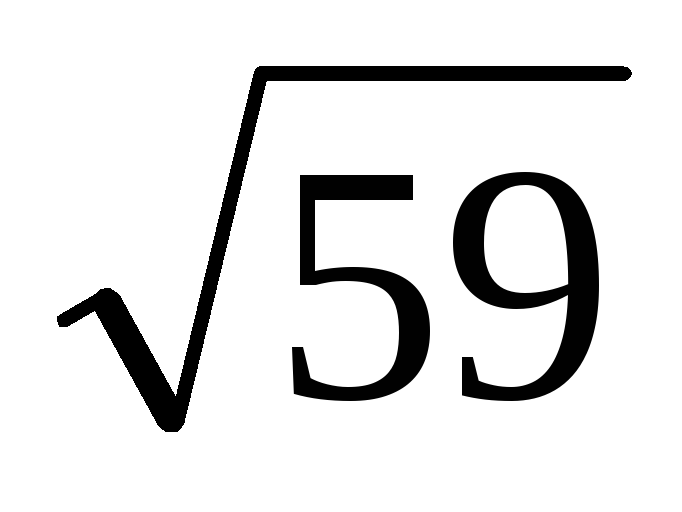Варіант 4.

1. Довести, що сума квадратів п’яти послідовних цілих чисел не може бути квадратом цілого числа.

2. Довести, що якщо a²+ b² ділиться на 7, де a і b –цілі числа, то а ділиться на 7 і b ділиться на 7.

3. Довести, що три числа а, a+m, a+n не можуть бути одночасно простими, якщо a>3 і натуральні числа m і n дають при діленні на 3 остачі, відповідно рівні 1 і 2.

4. Знайти натуральні числа a і b, якщо a+b=144; (a,b)=24.

5. Знайти кількість натуральних чисел, які менші від числа 1476 і мають з ним НСД число 41.

6. Скількома нулями закінчується число 100!?

7. Знайти x, якщо (х)=12.

8. Розв’язати конгруенцію 39x 84(mod 93).

9. Розв’язати у цілих числах рівняння 43x-37y=21.

10. Скоротити дріб : .

11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення .

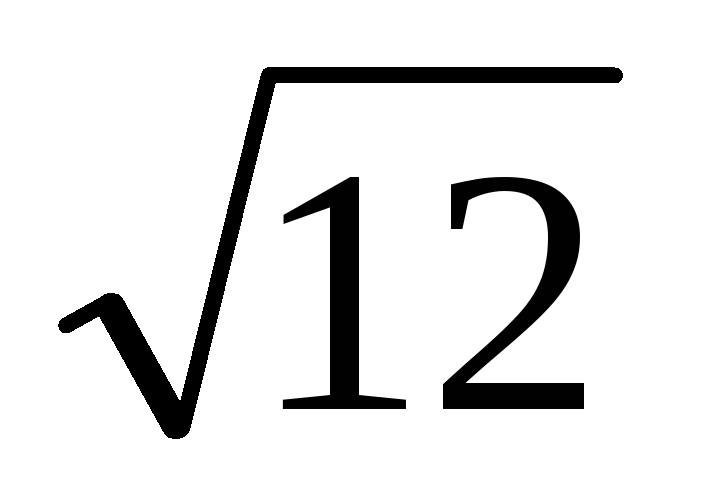Варіант 5.

1. Довести, що якщо чисельник дробу є різниця квадратів двох непарних чисел, а знаменник - сума квадратів тих же чисел, то такий дріб завжди скоротний на 2, але нескоротний на 4.

2. Довести, що сума кубів трьох послідовних цілих чисел ділиться на 9.

3. Довести, що з усіх цілих чисел виду 2р+1, де р- просте число, тільки одне число є точним кубом.

4. Сума двох чисел 667, а відношення НСК до їх НСД дорівнює 120.Занйти ці числа.

5. Знайти кількість натуральних чисел, які менші від числа 975 і мають з ним НСД число 13.

6. Знайти останні дві цифри числа 2¹⁰⁰.

7. Знайти натуральне число n, якщо n ділиться тільки на два простих числа і τ(n)=6, a σ(n)=42.

8. Розв’язати конгруенцію 12x 51(mod 39).

9. Розв’язати у цілих числах рівняння 17x-16y=31.

10. Скоротити дріб : .

11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення .

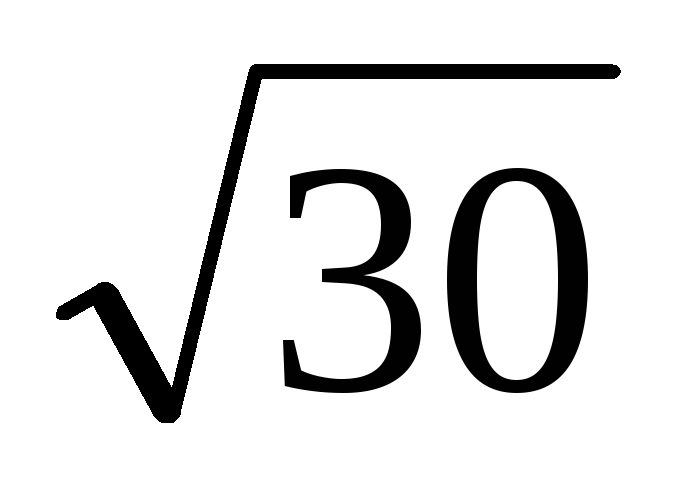Варіант 6.

1. Знайти чотиризначне число, яке є точним квадратом, у якого цифра тисяч однакова з цифрою десятків, а цифра сотень на 1 більша за цифру одиниць.

2. Довести, що числа виду 3k+2, kZ не можуть бути квадратами цілих чисел.

3. Довести, що існує нескінченна множина простих чисел виду р=6k-1.

4. Знайти натуральні числа a і b, якщо 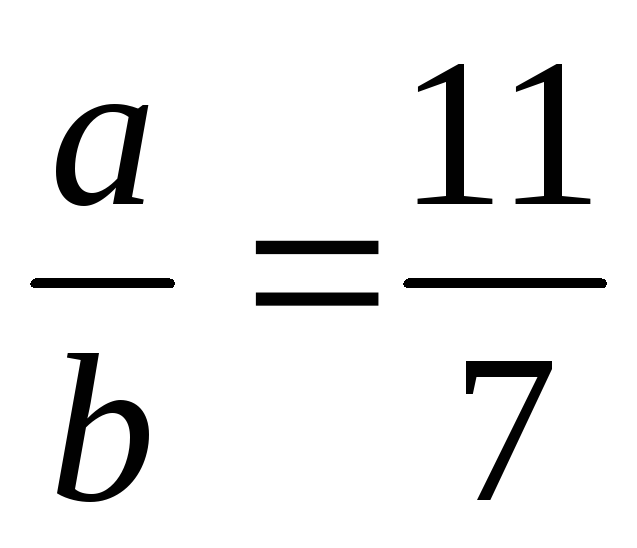, (a,b)=45.

5. Знайти кількість натуральних чисел, які менші від числа 1072 і мають з ним НСД число 8.

6. Знайти остачу від ділення 439²⁹¹ на 60.

7. Знайти число N, добуток усіх дільників якого дорівнює 3³⁰5⁴⁰.

8. Розв’язати конгруенцію 20x 10(mod 25).

9. Розв’язати у цілих числах рівняння 53x-17y=25.

10. Скоротити дріб : .

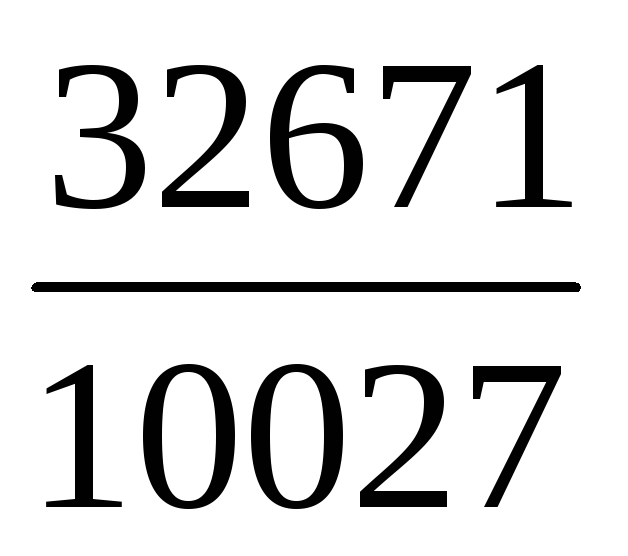11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення .

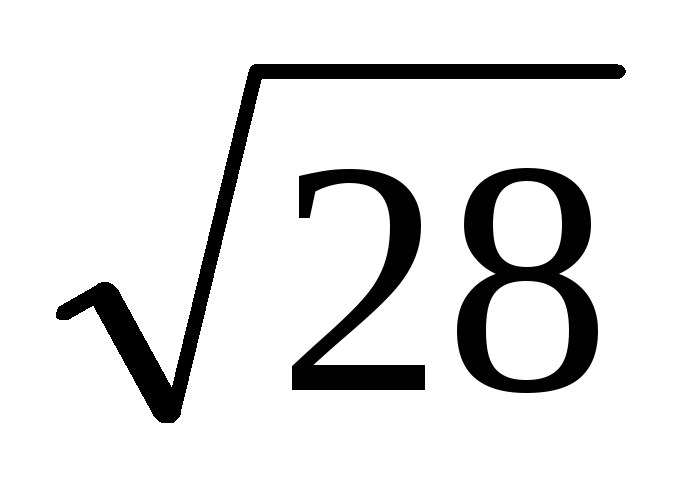Варіант 7.

1. Довести, що (n³-1)7, або (n³+1)7, якщо n не ділиться на 7, nZ.

2. Довести, що при натуральному n сума 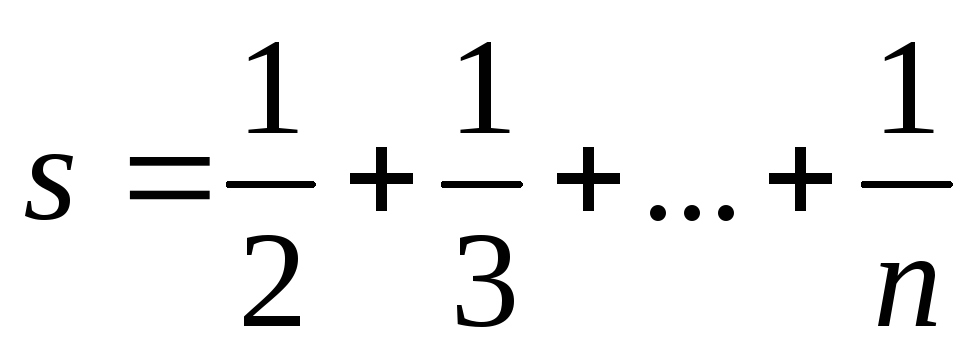не може біти цілим числом.

3. Довести, що якщо p і q - прості числа, більші за 3, то p²-q² кратне 24.

4. Знайти натуральні числа a і b, якщо 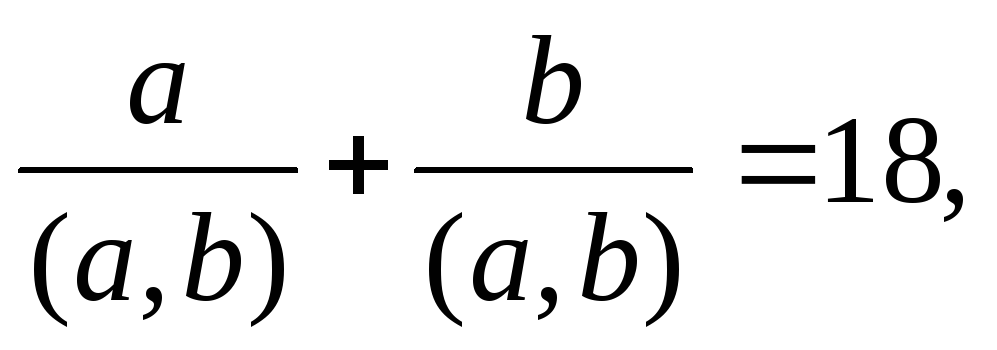[a,b]=975.

5. Знайти кількість натуральних чисел, які менші від числа 2476 і мають з ним НСД число 619.

6. Знайти остачу від ділення 93⁴¹ на 111.

7. Знайти натуральне число n, якщо n ділиться тільки на два простих числа і τ(n)=12, a σ(n)=465.

8. Розв’язати конгруенцію 5x 26(mod 12).

9. Розв’язати в цілих числах рівняння 23x-15y=19.

10. Скоротити дріб : .

11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення .

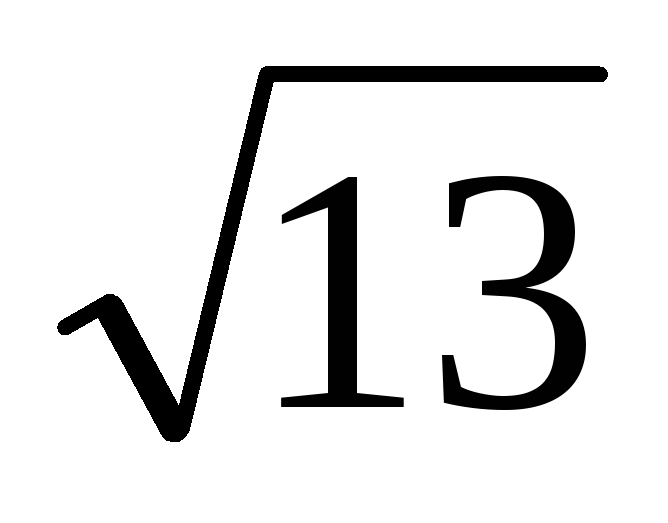Варіант 8.

1. Знайти усі натуральні числа n, для яких число n²+1 ділиться на n+1.

2. Довести, що для кожного натурального числа n число 3(1⁵+2⁵+...+n⁵) ділиться на число (1³+2³+...+n³).

3. Знайти значення простого числа р, якщо p+10 і p+14 - прості числа.

4. Знайти натуральні числа a і b, якщо 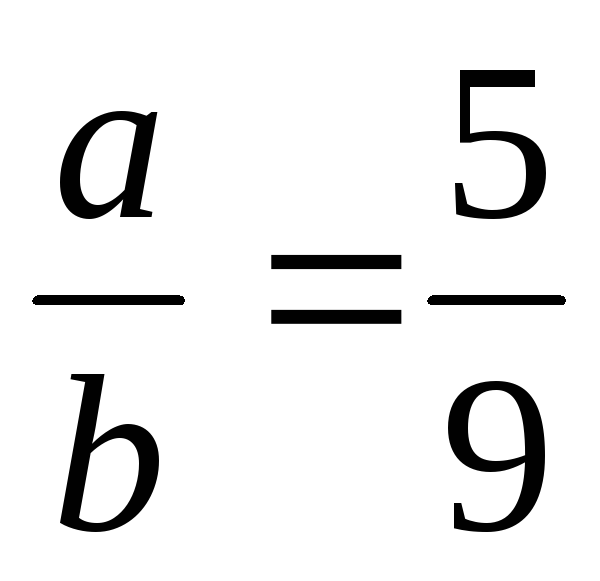, (a,b)=28.

5. Знайти кількість натуральних чисел, які менші від числа 975 і мають з ним НСД число 13.

6. Знайти остачу від ділення 439²⁹¹ на 60.

7. Розв’язати конгруенцію 29x 3(mod 12).

8. Знайти число N, добуток усіх дільників якого дорівнює 5832.

9. Розв’язати в цілих числах рівняння 41x-114y=5.

10. Скоротити дріб : .

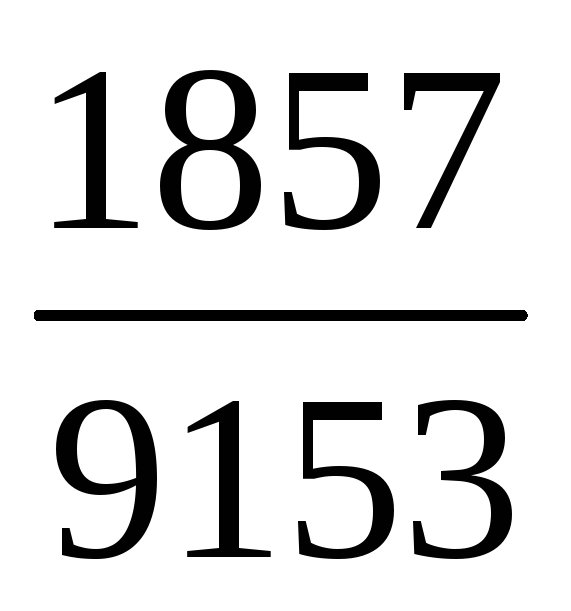11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення .

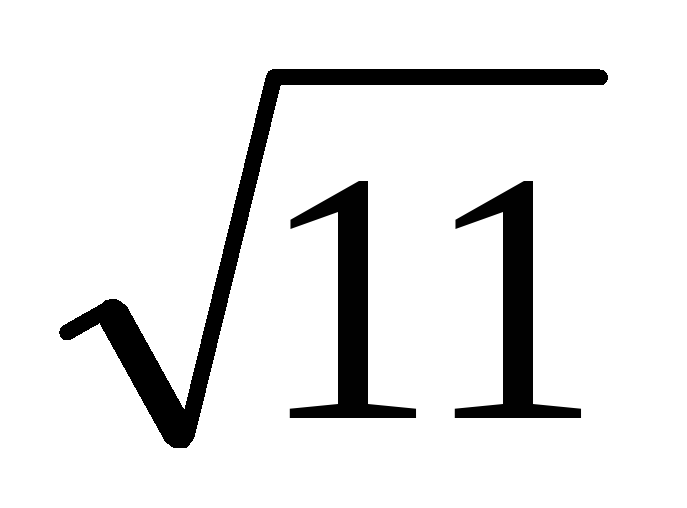Варіант 9.

1. Довести, що якщо mn+pq ділиться на m-p, то і mq+np ділиться на m-p, де m,n,p,q – цілі числа.

2. Довести, що сума квадратів двох послідовних цілих чисел, при діленні на 4 дає остачу 1.

3. Знайти всі прості числа, які є одночасно сумами і різницями простих чисел.

4. Знайти натуральні числа a і b, якщо (a,b)=24; [a,b]=2496.

5. Знайти кількість натуральних чисел, менших від числа 1072 і мають з ним НСД число 8.

6. Знайти натуральне число n, якщо n=pq, де p і q - різні прості числа, такі, що p-q=2 і φ(n)=120.

7. Розв’язати конгруенцію 16x 50(mod 23).

8. Розв’язати в цілих числах рівняння 47x-105y=4.

9. Знайти дві останні цифри числа 2¹⁵³.

10. Скоротити дріб : .

11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення .

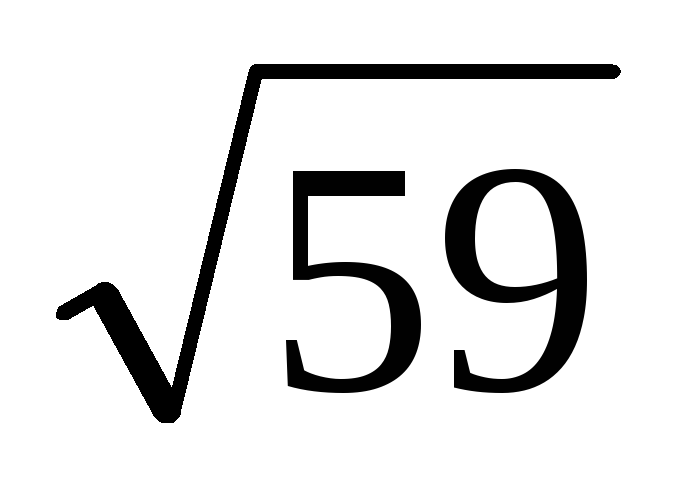Варіант 10.

1. Довести, що (2²ⁿ-6)10, для будь-якого натурального числа n≥2.

2. Нехай p – просте число і р≥5. Довести, що (р²-1)24.

3. Довести, що сума квадратів двох непарних чисел не може бути квадратом цілого числа.

4. Знайти натуральні числа a і b, якщо ab=168; (a,b)=14.

5. Знайти кількість натуральних чисел, які менші від числа 975 і мають з ним НСД число 13.

6. Знайти кількість нулів, якими закінчується число 295!

7. Знайти натуральне число n, якщо n ділиться на 12 і τ(n)=14.

8. Розв’язати конгруенцію 15x 3(mod 45).

9. Розв’язати в цілих числах рівняння 17x-16y=31.

10. Скоротити дріб : .

11. Розкласти в ланцюговий дріб і обчислити з точністю до 0,0001 значення .
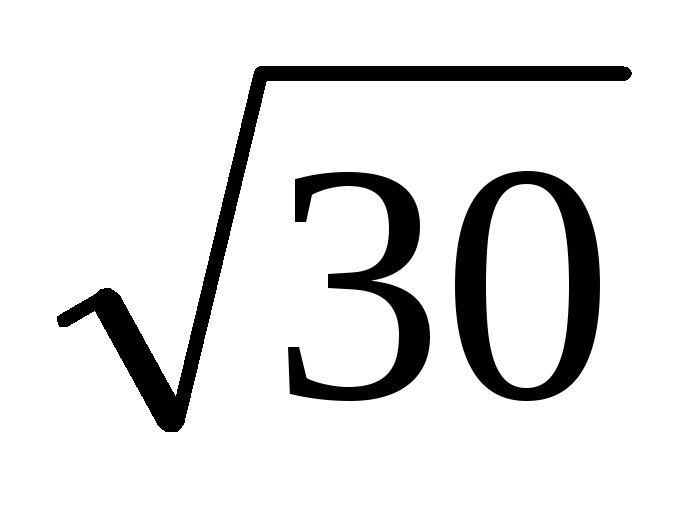