21.6. Енергія гармонічного коливання

Розглянемо тепер на прикладі пружинного маятника процеси зміни енергії в гармонічному коливанні.

Очевидно, що повна енергія пружинного маятника

.

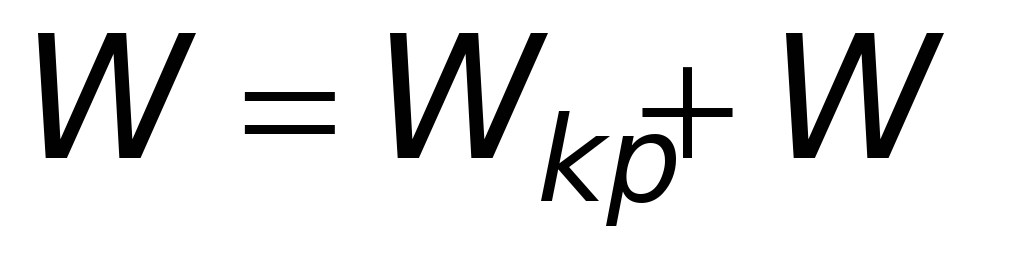де кінетична W_k і потенціальна W_p енергії визначаються виразми:

Оскільки , то вираз для потенціальної енергії можна представити у вигляді

.

Рис. 21.6

Залежності від часу кінетичної та потенційної енергії гармонічних коливань показані на рис. 21.6.

Повна енергія гармонічного коливання не залежить від часу:

(21.13)

Зауважимо, що енергія коливань пропорційна квадрату їх частоти. Ця залежність знаходить практичне застосування при використанні високочастотних коливальних процесів для збільшення потужності машин і механізмів без збільшення їхніх розмірів і маси (ультразвукові методи обробки матеріалів, використання високочастотних електродвигунів тощо.).

21.7. Коливальний контур

Розглянемо тепер принципово інший тип коливань – коливання електричних зарядів і струмів у коливальному контурі.

Рис. 21.7

Ідеальний коливальний контур (тобто такий контур, у якому відсутній омічний опір) складається з котушки індуктивності й конденсатора (рис. 21.7). Якщо конденсатор попередньо заряджений, то при замиканні контуру в ньому потече струм. На підставі другого закону Кірхгофа можна записати:

(21.14)

де — напруга на обкладках конденсатора, а — ЕРС самоіндукції. Підставивши значення і в (21.14) дістанемо:

.

(21.15)

На підставі того, що , рівняння (21.15) можна перетворити до вигляду

.

(21.16)

Зіставляючи (21.16) і (21.6), можна встановити, що заряд на обкладках конденсатора буде змінюватися за гармонічним законом

с циклічною частотою . Звідси випливає відома формула Томсона, що визначає період коливань заряду в контурі:

.

(21.17)

Із зіставлення формули Томсона з періодом коливань пружинного маятника (§21.3) можна встановити аналогію між механічними та електричними параметрами коливальних систем: аналогом маси є індуктивність, а роль жорсткості (коефіцієнта пружності) у коливальному контурі виконує величина 1/C.

У процесі коливань пружинного маятника відбувається перетворення кінетичної енергії в потенціальну . Аналогічні перетворення енергії відбуваються в коливальному контурі: енергія магнітного поля котушки перетворюється в енергію електричного поля конденсатора і навпаки. В ідеальному контурі або , звідки

.

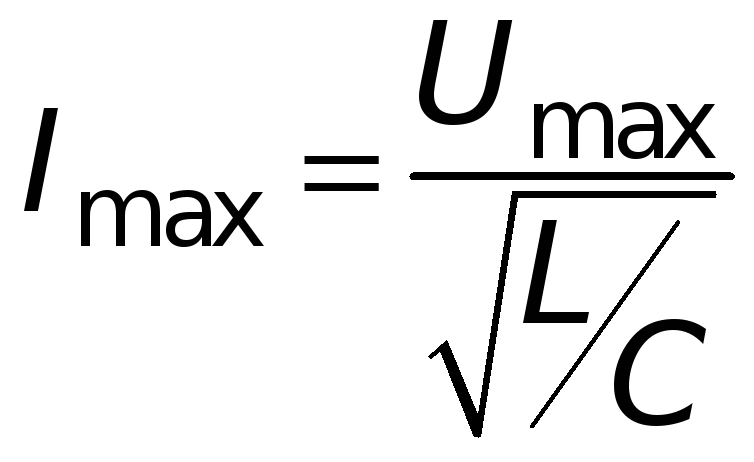В останньому виразі величина відіграє роль опору й називається хвильовим опором контуру.

21.8. Додавання скалярних коливань

У загальному випадку коливальна система може одночасно виконувати кілька коливальних рухів. Для описання таких рухів застосовне одне з найважливіших положень, що характеризують гармонічні коливання — принцип суперпозиції: якщо x₁(t) і x₂(t) — зміщення, що виникають під дією збурювальних сил F₁(t) і F₂(t), то результуюче зміщення x(t) =x₁(t) + x₂(t) буде виникати під дію сили F(t)= F₁(t) + F₂(t). Якщо система виконує кілька коливань, то ці коливання складаються незалежно одне від одного.

Розглянемо спочатку додавання скалярних коливань, тобто коливань скалярних фізичних характеристик (тиску, температури, щільності, заряду тощо). У випадку механічних коливань скалярними є коливання, що відбуваються уздовж однієї з осей координат.