26.3. Дифракція плоских хвиль (дифракція Фраунгофера)

Цей вид дифракції спостерігається в паралельних променях. На шляху цих променів поставимо екран з вузькою нескінченно довгою щілиною (у реальних умовах необхідно, щоб ширина щілини була значно менше її довжини). Промені, що пройшли крізь щілину, збираються лінзою. Дифракційна картина спостерігається на екрані, поміщеному у фокальній площині лінзи (рис. 26.6).

Оптична різниця ходу  між крайніми променями MA і NB, що відхилилися на кут , становить

,

(26.9)

де a — ширина щілини.

Розіб'ємо щілину MN на зони Френеля у вигляді вузьких смужок, паралельних ребру щілини, так щоб різниця ходу від країв цих зон відрізнялася на /2. Число таких зон буде рівнятися . Як і в попередньому випадку (§26.2), результуюча амплітуда коливань у точці P визначається знакозмінною сумою:

Ep = E1 – E2 + E3 – …  En...

(26.10)

У цьому випадку всі зони Френеля рівні по площі й нахилені під одним і тим же кутом у напрямку спостереження, тому

E₁ = E₂ = … = E_n = E...

Рис. 26.6

Результат підсумовування в (26.10) залежить від того, парне чи непарне число зон Френеля укладається на ширині щілини (число таких зон залежить від кута спостереження ).

Нехай на ширині щілини укладається парне число зон, тобто

(26.11)

Легко бачити, що в цьому випадку сума

E_p = E – E + E – … – E = 0...

Отже, якщо оптична різниця ходу між крайніми променями дорівнює парному числу довжин напівхвиль (або, що те ж саме, на ширині щілини укладається парне число зон Френеля), то в даному напрямку спостерігається дифракційний мінімум. Зони в цьому випадку попарно гасять одна одну.

І навпаки, якщо на ширині щілини укладається непарне число зон, тобто

,

(26.12)

то

E_p = E – E + E – … + E = E...

Отже, якщо оптична різниця ходу між крайніми променями дорівнює непарному числу напівхвиль (або, що те ж саме, на ширині щілини укладається непарне число зон Френеля), то в даному напрямку спостерігається дифракційний максимум. У цьому випадку одна із зон залишається нескомпенсованою.

Розрахунки показують, що інтенсивності центрального й наступного максимумів відносяться як 1:0,047:0,017:..., тобто основна частина світлової енергії зосереджена в центральному максимумі (рис. 26.6).

26.4. Дифракційна решітка

Рис. 26.7

При розгляді дифракції на одній щілині ми бачили, що основна частка інтенсивності доводиться на центральний максимум, а дифракційна картина виходить більш-менш розмитою. Крім того, якщо скористатися щілиною як спектральним приладом, то його світлосила виявляється дуже малою.

Для усунення цих недоліків застосовують дифракційну решітку, тобто сукупність паралельних щілин однакової ширини a, розділених однаковими по ширині b непрозорими проміжками. Величина a+b=l називається періодом дифракційної решітки.

Розглянемо спочатку дифракційну решітку, що складається із двох щілин (рис. 26.7). Промені 1-1' і 2-2' називаються відповідними. Різниця ходу між двома відповідними променями

,

(26.12)

Очевидно, що умова мінімуму для однієї щілини зберігається й для дифракційної решітки:

.

(26.13)

Стосовно до дифракційної решітки умова (26.13) - це умова виникнення головних мінімумів. У результаті інтерференції відповідних променів, крім того, виникають додаткові мінімуми. При цьому

,

(26.14)

тобто різниця ходу між відповідними променями дорівнює непарному числу довжин напівхвиль.

Між додатковими мінімумами розташовуються так звані головні максимуми. Їх можна спостерігати в тих напрямках, де дію однієї щілини підсилює дія іншої. Точніше, головні максимуми спостерігаються в тому випадку, коли оптична різниця ходу між відповідними променями дорівнює парному числу довжин напівхвиль:

,

або

.

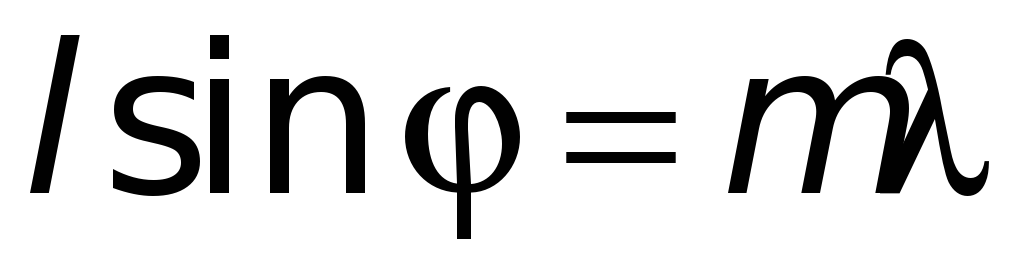(26.15)

Таким чином, повна дифракційна картина від двох щілин описується наступними співвідношеннями:

головні мінімуми — a sin  = m;

додаткові мінімуми — ;

головні максимуми — l sin  = m.

У випадку, якщо дифракційна решітка складається з N щілин, умови для головних мінімумів і головних максимумів зберігаються, а умова для додаткових мінімумів узагальнюється:

.

(26.16)

Рис. 26.8

де m приймає цілочислові значення, крім m = 0, N, 2N, ... , тобто крім тих значень, при яких умова (26.16) переходить в (26.15).

Отже, у випадку N щілин між двома головними максимумами розташовуються N-1 додаткових мінімумів, розділених вторинними максимумами, що створюють досить слабке тло (рис. 26.8). З ростом числа щілин N зростає інтенсивність світла, що пройшло через решітку.

При цьому число мінімумів між головними максимумами зростає й, отже, головні максимуми будуть більш інтенсивними і більш гострими (див. рис. 26.8, де показана дифракційна картина на одній, двох, чотирьох і восьми щілинах).

Положення головних максимумів залежить від довжини хвилі  (див. формулу (26.15)). Тому, якщо на дифракційну решітку падає біле світло, то вона розкладає його в спектр. При цьому, чим більше довжина хвилі , тим на більший кут відбувається відхилення (рис. 26.9). При m=1 одержуємо спектр першого порядку, при m=2 — спектр другого порядку і т.д. Спектри другого й третього порядку можуть частково перекриватися. Чим більше порядок спектра, тим менше його інтенсивність. На практиці звичайно використають спектри першого та другого порядків.

Таким чином, дифракційна решітка є спектральним приладом і служить для визначення спектрального складу світла.

Рис. 26.9

На закінчення розглянемо одну з найважливіших характеристик дифракційної решітки – її роздільну здатність.

Роздільною здатністю спектрального приладу називають безрозмірну величину

,

Рис. 26.10

де — абсолютне значення мінімальної різниці довжин хвиль двох сусідніх спектральних ліній, при якій ці лінії реєструються роздільно. Відповідно до критерію Релея, роздільна реєстрація двох спектральних ліній можлива, якщо інтенсивність провалу становить 80 % інтенсивності в максимумі (рис. 26.10, а). Якщо критерій Релея не виконується, то роздільне спостереження ліній неможливо (рис. 26.10, б).

Можна показати, що для дифракційної решітки R=mN, тобто роздільна здатність дифракційної решітки пропорційна порядку спектра m і числу щілин N. Для сучасних решіток R ~ 2·10⁵.