25.2. Розрахунок інтерференційної картини від двох когерентних джерел

З'ясуємо умови виникнення інтерференційних максимумів або мінімумів при інтерференції хвиль від двох когерентних джерел S₁ і S₂. У загальному випадку ці джерела можуть перебувати в різних середовищах з показниками заломлення n₁ і n₂. При цьому оптичні когерентні джерела випромінюють світлові хвилі з однаковою частотою , але різними довжинами хвиль:

,

де — довжина світлової хвилі у вакуумі.

У точці P (рис. 25.2) накладаються дві хвилі, рівняння яких

,	(25.1)
,	(25.2)

де x₁ і x₂ — відстані від джерел до розглядуваної точки P, причому вектори й напрямлені однаково (наприклад, перпендикулярно до площини креслення).

Рис. 25.2

Розрахунок результуючої амплітуди і відповідно інтенсивності світлової хвилі в точці P можна виконати як додавання скалярних коливань однакової частоти (див. §  21.8).

Різниця фаз коливань, що додаються, на підставі (25.1) і (25.2) становить

.

Виразивши довжини хвиль _ і ₂ через довжину хвилі у вакуумі, можна записати

.

Різниця  = n₂x₂ – n₁x₁ називається оптичною різницею ходу. Таким чином, різниця фаз

.

(25.3)

Підставивши (25.3) в (21.24), знайдемо значення результуючої амплітуди коливань у точці P

,

(25.4)

Розглянемо окремі випадки.

1. Оптична різниця ходу дорівнює цілому числу напівхвиль:

	(25.5)
;
;
.	(25.6)

З (25.6) видно, що в цьому випадку результуюча амплітуда коливань дорівнює сумі амплітуд, тобто відбувається взаємне посилення коливань і інтенсивності. Таким чином, умова (25.5) є умова виникнення інтерференційного максимуму.

2. Оптична різниця ходу дорівнює непарному числу напівхвиль:

	(25.7)
;
;
.	(25.8)

З (25.8) видно, що результуюча амплітуда коливань дорівнює різниці амплітуд, тобто відбувається взаємне ослаблення амплітуд коливань. У випадку, якщо E₀₁ = E₀₂, відбувається повне гасіння, тобто E_p = 0. Таким чином, умова (25.7) є умова виникнення інтерференційного мінімуму.

25.3. Інтерференція в тонких плівках

Рис. 25.3

Важливим у практичному відношенні випадком інтерференції світлових хвиль є інтерференція світла в тонких плівках.

Нехай на поверхню розташованої в повітрі тонкої прозорої плівки товщиною h і з показником заломлення n падає світловий промінь (рис. 25.3). У точці A світловий промінь частково відбивається (промінь 1') і частково заломлюється. Заломлений промінь відбивається в точці B і повертається назад — промінь 2'. Промені 1' і 2' когерентні, тому що вони утворилися в результаті поділу одного й того самого падаючого променя. Оптична різниця ходу між ними

.

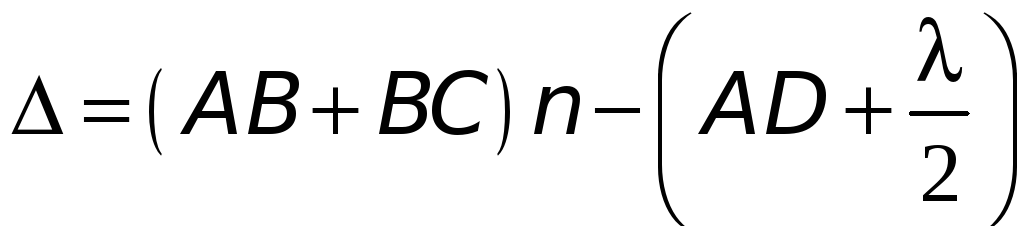(25.9)

Необхідність врахування додаткового доданка /2 пов'язана з тим, що умови відбиття світлових променів у точках A і B різні. У точці A відбиття походить від оптично більш щільного середовища; при цьому фаза світлової хвилі змінюється на , що еквівалентно різниці ходу /2. У точці B світлова хвиля відбивається від оптично менш щільного середовища і її фаза при цьому не змінюється.

З рис. 25.3 видно, що

Підставивши ці вираз в (25.9) і замінивши за допомогою закону заломлення (24.16) кут заломлення  на кут падіння , після нескладних перетворень дістанемо

.

(25.10)

З (25.10) видно, що оптична різниця ходу залежить від трьох параметрів: товщини плівки h, кута падіння  і довжини хвилі , тобто  = f(h, , ). Для аналізу результату інтерференції розглянемо окремі випадки, коли одні з параметрів змінний, а інші фіксовані.

1. Нехай h=const, =const, ≠const, тобто на плівку постійної товщини під тим самим кутом падає біле світло. Тоді, залежно від довжини хвилі, буде виконуватися або умова максимуму (25.5), або умова мінімуму (25.7). Внаслідок цього плівка у відбитому світлі буде пофарбованою - будуть видні ті кольори (ізохроми), яким відповідають довжини хвиль, що задовольняють умові максимуму. Додаткові кольори будуть видні в проходячому світлі: цим кольорам відповідають довжини хвиль, які задовольняють умові мінімуму у відбитому світлі й умові максимуму – в проходячому світлі.

Рис. 25.4

2. Нехай h=const, const, =const, тобто на плівку постійної товщини під різними кутами падає монохроматичне світло. У цьому випадку на плівці у відбитому світлі будуть видні світлі й темні смуги. Ці смуги називаються лініями рівного нахилу, тому що кожна з них проходить по таких місцях плівки, де кут падіння один і той самий: світлі смуги відповідають кутам нахилу, що задовольняє умові максимуму, темні — умові мінімуму. Різним лініям відповідають різні, але постійні кути падіння. Якщо джерело точкове, то на плівці будуть видні концентричні темні й світлі кола (рис. 25.4).

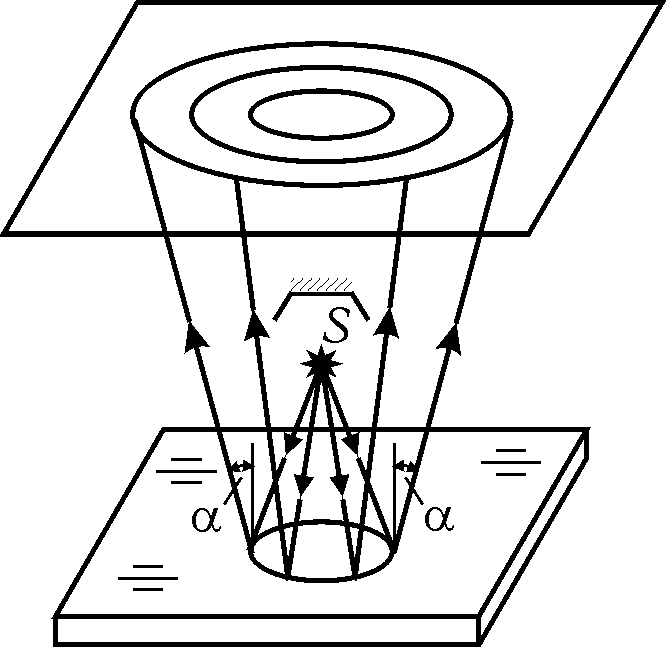
3. Нехай hconst, =const, =const, тобто на плівку змінної товщини під одним і тим же кутом падає монохроматичне світло. На плівці будуть видні темні й світлі смуги, кожна з яких проходить по таких її місцях, де товщина одна і та сама (лінії рівної товщини). Різним лініям відповідають різні, але сталі товщини. Якщо, наприклад, взяти дротовий каркас із мильною плівкою й поставити його вертикально, то за рахунок стікання рідини вона набирає форми клина і на ній будуть видні горизонтальні світлі й темні смуги.

Явище інтерференції світла в тонких плівках лежить в основі просвітління оптики. Сучасні оптичні прилади (об'єктиви фотоапаратів, біноклі, секстанти, перископи й тощо.) містять велику кількість оптичних елементів (лінз, призм тощо Проходження світла через кожний з таких елементів супроводжується частковим відбиттям, що може привести до істотного (до 40 %) втраті інтенсивності. Для зменшення втрат на відбиття на поверхню оптичних елементів наносять тонку плівку речовини, підбираючи її товщину так, щоб різниця ходу відбитих променів задовольняла умові мінімуму. Крім того, як показують теоретичні розрахунки, для повного гасіння відбитих променів необхідно підібрати плівку з показником заломлення, рівним кореню квадратному з показника заломлення скла. При виконанні цих умов відбиття припиняється, що істотно збільшує світлосилу оптичних приладів.