Задача 13

Методом вращения вокруг оси, параллельной плоскости проекций, определить истинную величину плоской фигуры.

Индивидуальное задание представлено на рис.13.1.

Для решения этой задачи необходимо вспомнить материал раздела 4.4. «Проецирование плоских фигур. Пересечение плоских фигур» учебного пособия [3]. Если плоская фигура задана многоугольником с количеством сторон, большим чем три, то первоначально необходимо построить недостающие проекции вершин так, чтобы все точки этой фигуры находились в одной плоскости. Например, четырехугольник может быть задан двумя проекциями трех его вершин и лишь одной проекцией четвертой вершины (рис.13.2). Недостающая проекция вершины лежит на пересечении линии проекционной связи, проведенной из имеющейся проекции вершины многоугольника, и проекции диагонали, проходящей, в свою очередь, через точку пересечения диагоналей (рис.13.3).

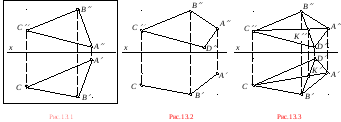
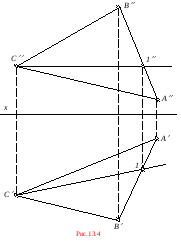
1. Для нахождения истинной величины заданного треугольника ABC повернем его вокруг горизонтали в положение, параллельное плоскости проекций ₁, тогда горизонтальная проекция фигуры будет представлять собой ее истинную величину^.

2. В плоскости ABC, например, через точку C проводим горизонталь C1 (рис.13.4):

C1  x; 1  AB.

Эту горизонталь принимаем за ось вращения. Точки, в том числе и вершина С треугольника, оказавшиеся на оси вращения, при вращении своего положения не меняют:

C  С.

3. Проводим плоскость вращения γ₁ точки В (рис.13.5): горизонтальный след плоскости вращения проходит через B и перпендикулярен C1 (эта плоскость является горизонтально-проецирующей; фронтальный след плоскости вращения для решения задачи не используется и на чертеже он не указан).

4. Определяем проекции центра вращения точки В (О_В) в пересечении плоскости вращения и оси вращения:

 =   C1;

  С1.

5. Радиус вращения точки В на горизонтальную (В) и фронтальную (В) плоскости проекций спроецирован с искажением. Определяем истинную величину радиуса вращения точки В (R_B) методом прямоугольного треугольника, одним катетом которого является горизонтальная проекция радиуса вращения В, а другим катетом расстояние, равное алгебраической разности координат z_В.

6. Определяем горизонтальную проекцию нового положения вершины В (В). На пересечении дуги окружности радиусом R_B, проведенной из , и следа плоскости вращения отмечаем В:

В    = R_В.

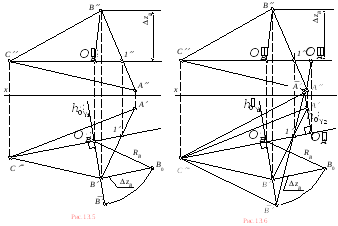
7. Для построения нового положения точки А не обязательно определять истинную величину ее радиуса вращения. Точка 1 (1  АВ) при вращении АВС остается неподвижной, поэтому новое положениеА можно найти в пересечении прямойВ1 с горизонтальным следом плоскости вращения точки А – (рис.13.6).

8. Соединив точки , и , получаем истинную величину заданного треугольника.

Задача 14

По истинной величине плоской фигуры, принадлежащей плоскости  и вписанной в окружность радиуса R с заданным центром О, построить ее проекции. Задачу решить способом совмещения.