Функция Лапласа

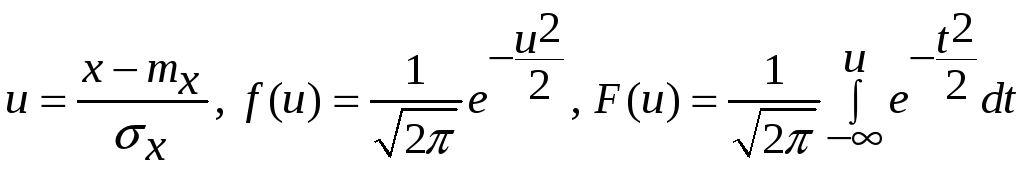- стандартное нормальное распределение с.в. от до . Проще рассматривать случай, когда .

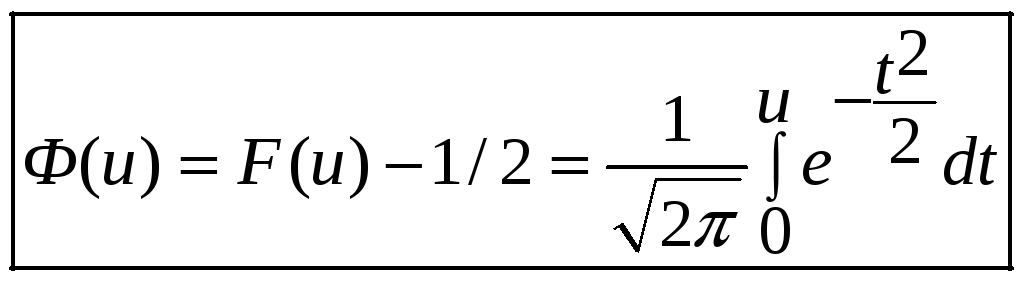
- табулированная функция Лапласа, широко используемая для определения вероятности попадания в диапазон значений:

.

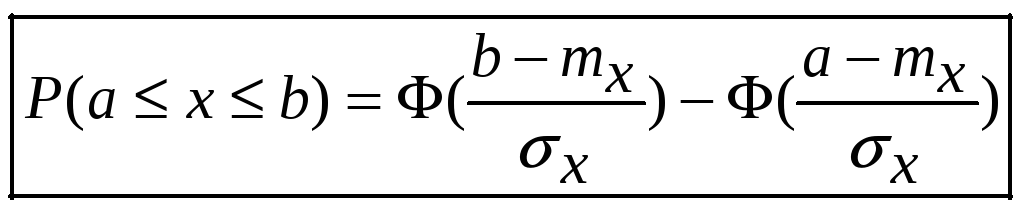Роль нормального распределения. Теоретики и практики («мифы»).

Центральная теорема: Сумма конечного числа нормальных с.в. есть нормальная с. в.

Центральная предельная теорема: Сумма бесконечного числа с.в. с любыми законами распределения, но с примерно одинаковыми дисперсиями, имеет нормальное распределение.

Многие экономические показатели имеют нормальный или близкий к нормальному закон распределения: доход населения, прибыль фирмы в отрасли и др.

Пример. В результате длительных наблюдений определено, что дивиденды и по акциям фирм и являются нормальными с. в.:; . Стоимость каждой акции равна 100$. Инвестор хочет приобрести акции на 1000 $.

а)Какие законы распределения имеют доходы X, Y от вложения всей суммы в акции фирмы А или В? б)Каков закон распределения имеет доход Z от покупки акций в пропорции 2/3? в)Построить графики функций случайных величин X, Y, Z. г)Какова вероятность того, что полученный доход Z от вложения будет лежать в пределах от 110$ до 150$?

а)X ~ (50;) или Y ~ (150, );

б) Z ~ (m_z=45+615=110, σ_z=);

в) При построении графиков целесообразно пользоваться правилом 3-х сигм и обязательно соблюдать условие нормировки (площадь под кривой распределения одна и та же - равна единице).

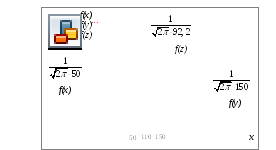
г)Р(110≤Z≤150)=Ф(0,43)-Ф(0)=0,16 (используются таблицы функции Лапласа).

Равномерное (равновероятное, прямоугольное)

распределение

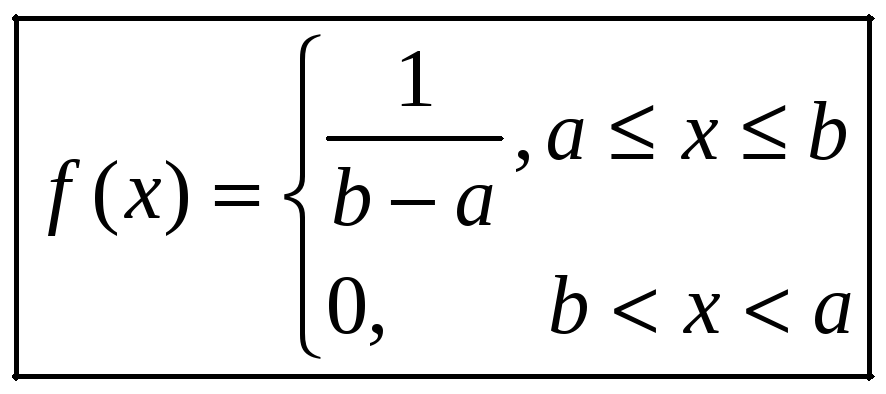
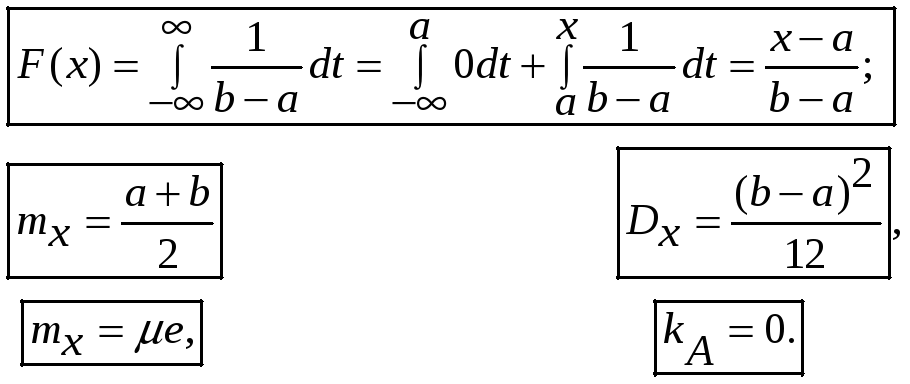
Показательное (экспоненциальное) распределение

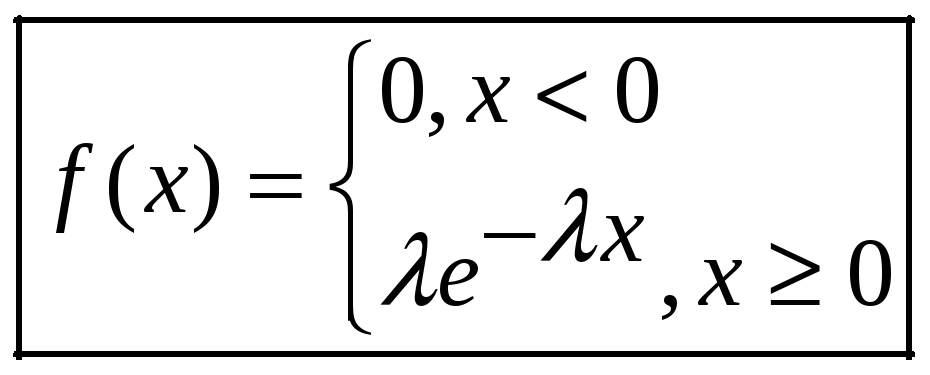
F(x)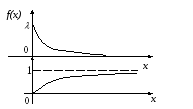

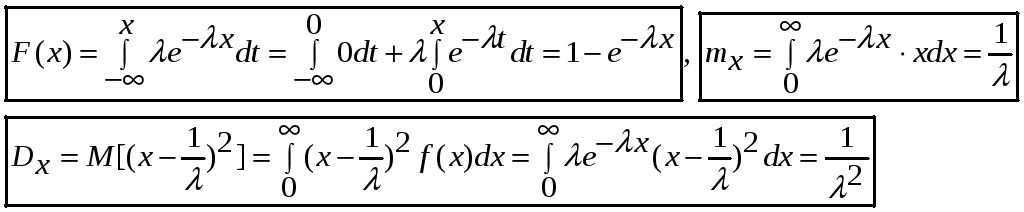
- характеристическое свойство показательного распределения

Приложение - функция надежности. Пусть объект анализа начинает функционировать в момент времени и по истечении выходит из строя. Обозначим через время безотказной работы. Тогда, вероятность отказа за время t равна:

Для оценки вероятности безотказной работы («накапливающиеся отказы») часто используется экспоненциальное распределение. При этом параметр распределения λ=λ(t) является функцией времени. Технические системы, в демографии – смертность.

«Внезапные отказы» - Гамма – распределение.

Распределение χ2

Сумма квадратов нормальных с.в. ~ (0,1) является с.в.

и имеет табулированное распределение χ² с числом степеней свободы. Здесь – число наложенных связей: обязательно - условие нормировки, и связи, связанные с расчетом тех или иных центральных или начальных моментов. Аналитическое выражение не приводится (сложное), распределение табулировано.

t - распределение (Стьюдента)

Если ~ (0,1), а ~χ² с степенями свободы, то с.в. 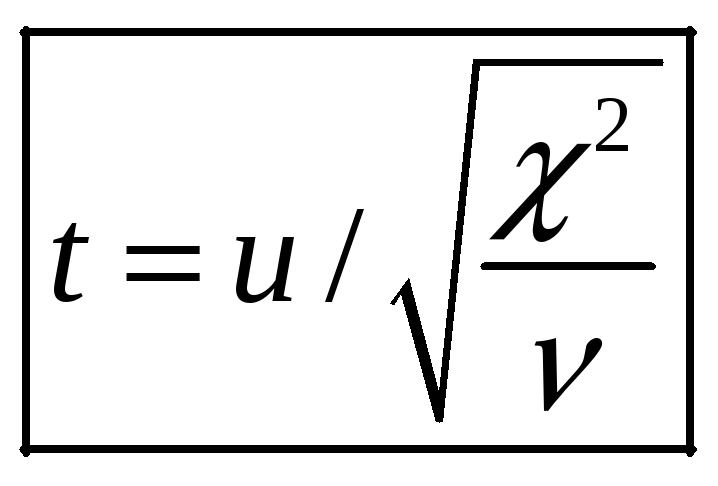имеет распределение Стьюдента с степенями свободы. . Основное распределение малых выборок (до 15 -17 – ти наблюдений). Распределение табулировано

F - распределение (Фишера)

Если и – независимые случайные величины, распределенные по закону χ² с степенями свободы и , соответственно, то с.в.

имеет распределение Фишера (табулировано).

В статистике широко используют прием введения некоторой случайной величины, распределение которой не зависит от числовых характеристик исходного анализируемого распределения. Такие величины имеют распределение Стьюдента, Фишера и .