Точечные оценки точности оценок (статистик) генеральных числовых характеристик

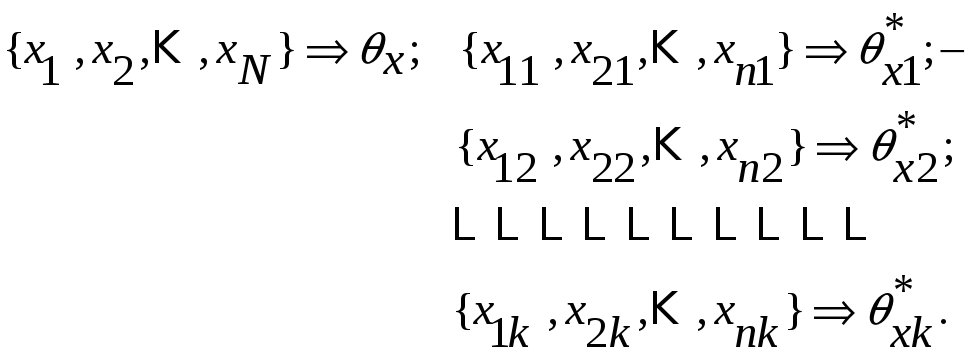-оценки статистических характеристик

- с.в., характеризуемая законами распределения и числовыми характеристиками распределения (обычно математическим ожиданием и дисперсией).

Можно говорить о распределении оценки матожидания, о матожидании оценки матожидания, о дисперсии оценки матожидания и т.д.

1. Оценка называется состоятельной, если она сходится по вероятности к оцениваемой характеристике.

2.Оценка называется несмещенной, если .

- смещение, систематическая погрешность (от смещенности)

Асимптотически несмещенная оценка

3.Оценка называется эффективной, если при используемом методе ее расчета выполняется условие .

Пример1. Оценка является несмещенной, а ее дисперсия уменьшается при усреднении в раз:

Если ~- эффективная оценка.

В прикладной статистике и в эконометрике, наибольшее внимание уделяют обеспечению эффективности и несмещенности оценок.

Пример 2. Оценка дисперсии является смещенной:

Доказано, что 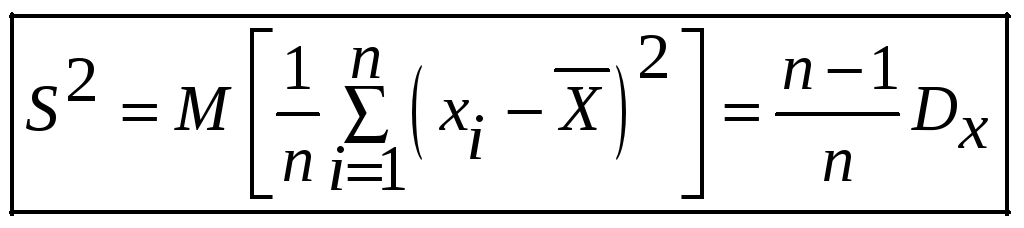- т.е. данный алгоритм дает смещенную оценку дисперсии: . Исправленная (несмещенная) оценка дисперсии

.

На практике исправленной оценкой дисперсии пользуются при

Интервальная оценка точности (надежность) генеральных

Математического ожидания и дисперсии

Д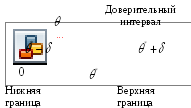оверительный интервал - интервал значений, в котором с заданной доверительной вероятностью (обычно назначают ) находится истинное значение оцениваемой статистической характеристики : .

Радиус доверительного интервала равен:,

- аргумент, соответствующий значению функции Лапласа, равной :

; - среднеквадратическое отклонение (его оценка).

Доверительный интервал случаен (зависит от конкретных выборок): случайно его положение на числовой оси и случайна его длина.

При , а при

Доверительный интервал для оценки математического ожидания

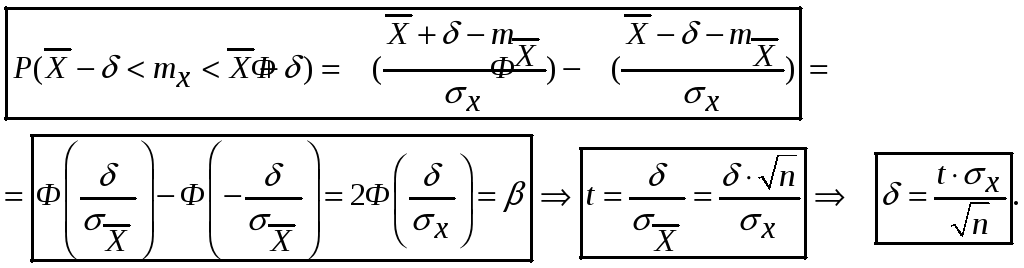
Здесь рассматривается как аргумент табулированной функции распределения Лапласа (нормальной !), при котором она равна значению : .

Значение генерального среднеквадратического отклонения редко известно, поэтому обычно в формуле используют оценку среднеквадратического отклонения, т.е. .

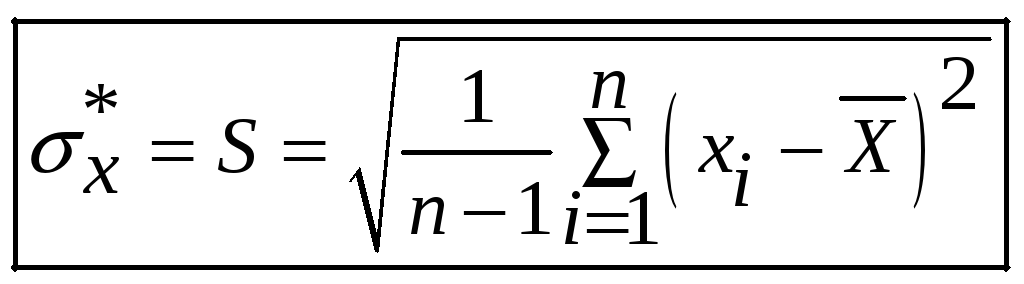Пример:~ Найти доверительный интервал для оценки неизвестного , при выборочном среднем , если объем выборки n=36, а .

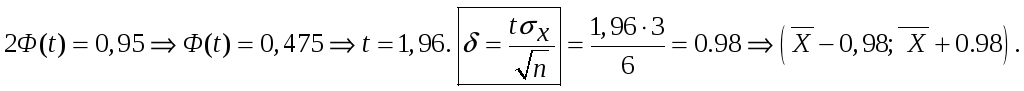
Замечание. Практически важной может быть задача определения объема выборки, которая обеспечит заданный радиус доверительного интервала: .

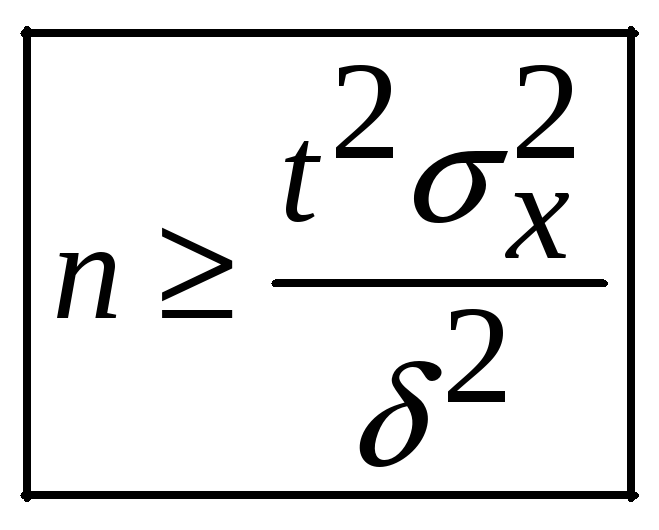Более точные результаты при малых объемах выборки и неизвестном дает использование распределения Стьюдента: для переменной - 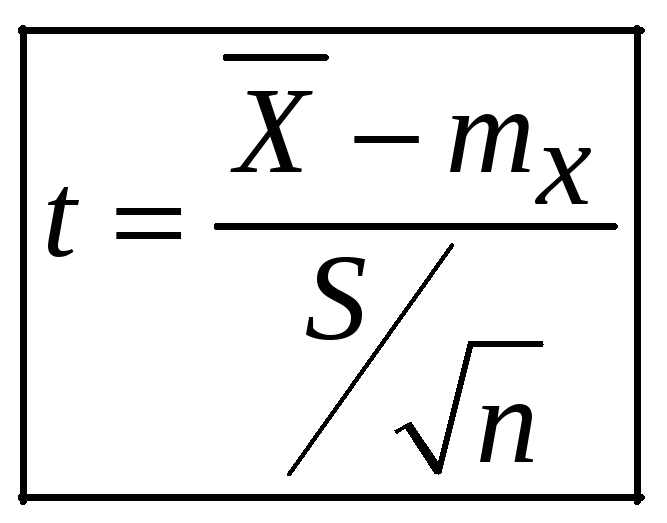, имеющей распределение Стьюдента с степенями свободы отклонение (~) Тогда доверительный интервал при неизвестном среднеквадратическом отклонении определяется следующим образом: 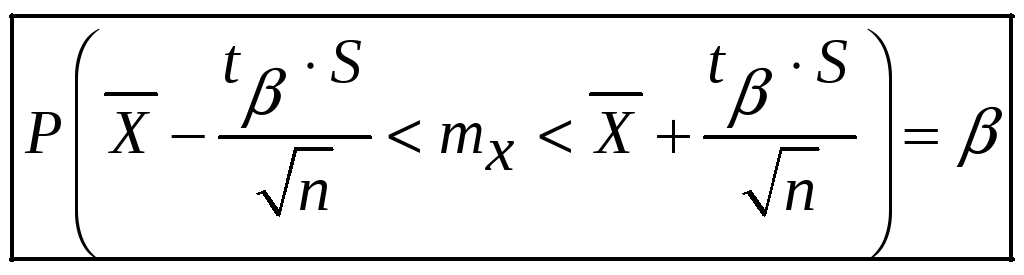, где аргумент табулированного распределения Стьюдента.

Доверительные интервалы оценки среднеквадратического отклонения

Пусть вновь ~, и - неизвестно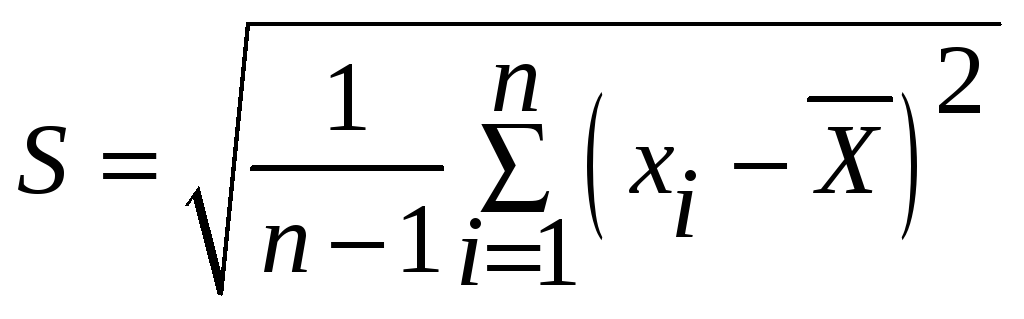, а . Тогда

где .

Доказано, что имеет табулированное распределение , независящее от параметров и исходного распределения, но зависящее от объема выборки и доверительной вероятности. Вычислив по выборке , находим по таблице , определяем границы доверительного интервала.