Распределения вероятностей дискретной случайной величины

, где - условие полноты группы

событий (нормировки)

			...
			...

ряд распределения, если наложено условие, => вариационный ряд

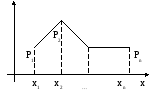График: многоугольник или

полигон распределения

Пример. В денежной лотерее выпущены 100 билетов. При этом могут быть 1 выигрыш по 50 руб., 10 выигрышей по 1 руб. Найти закон распределения. Пусть – величина возможного выигрыша при покупке 1 билета. =50 руб.=1/100;

	0	1	50
	0,89	0,1	0,01

=10 руб.=10/100;

=0 руб.=89/100.

Известно более 100 аналитических распределений

1.Биноминальное распределение _(схема испытаний Бернулли)

Пример. Монета брошена 2 раза. Определить закон распределения числа выпадения герба. Пусть – появление «герба». Тогда

;

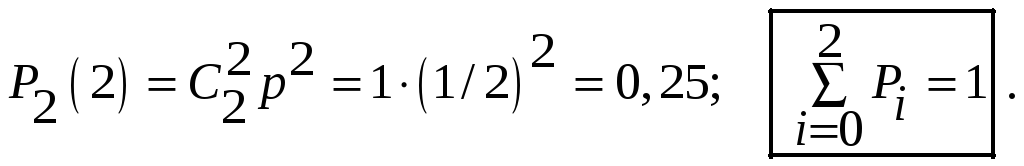
2.Распределение Пуассона

Схема испытаний Бернуллиформула Бернулли. При дополнительном условии локальная теорема Лапласа. При дополнительных условиях , вероятность «успехов» из испытаний определится асимптотической формулой Пуассона:

.

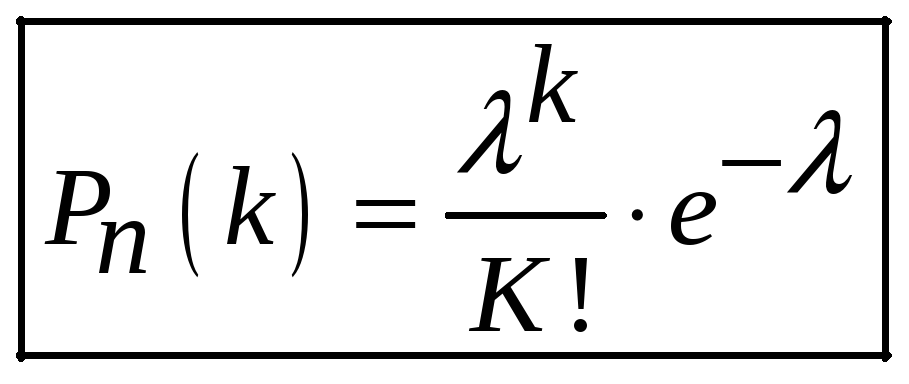Формула Пуассона широко используется в теории массового обслуживания и в теории надежности, где- имеет смысл интенсивности отказов.

Пример. Поставщик отправил дистрибъютеру 5000 товаров. Вероятность того, что единица товара выйдет из строя 0,0002. Найти вероятность того, что у дистрибъютера выйдут из строя 3 единицы товара.

. .

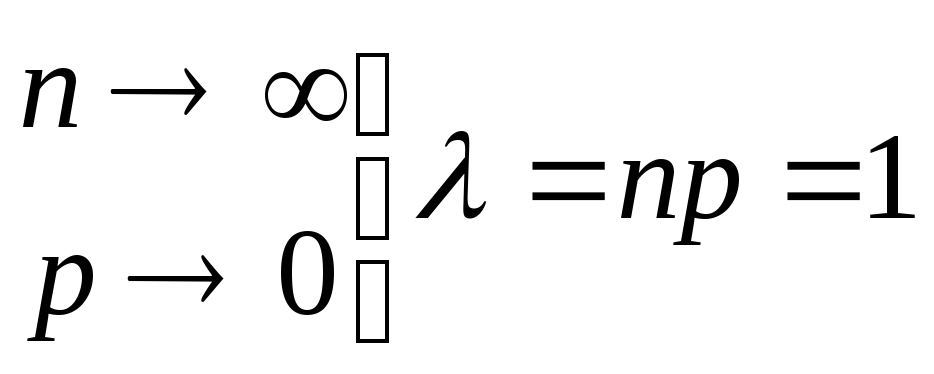
Основные формулы комбинаторики, используемые для определения вероятностей алгебры событий

Комбинаторика изучает количество комбинаций, подчиненных определенным условиям для элементов конечного множества.

1. Перестановками называют комбинации, составленные из одних и тех же элементов множества, отличающихся только порядком расположения .

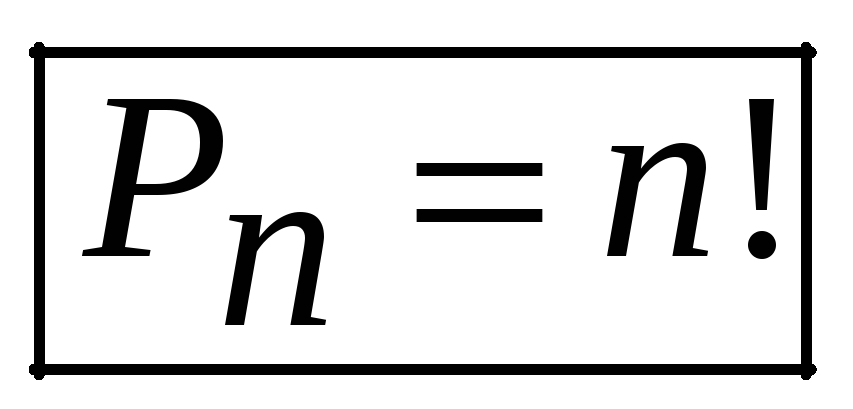Пример. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в число один раз.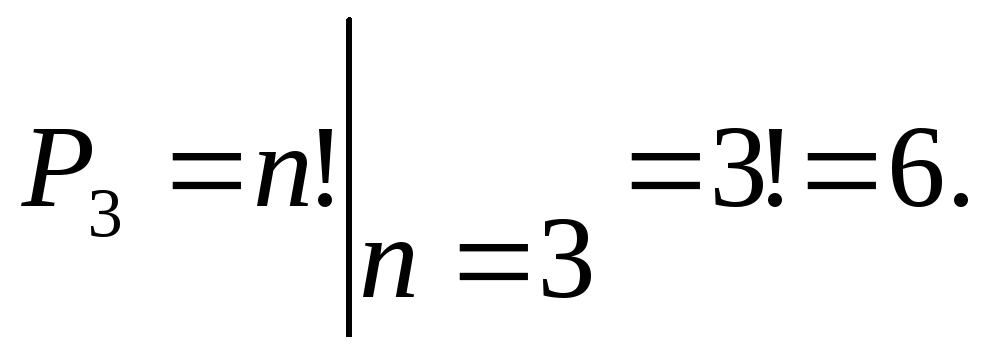

2. Размещениями 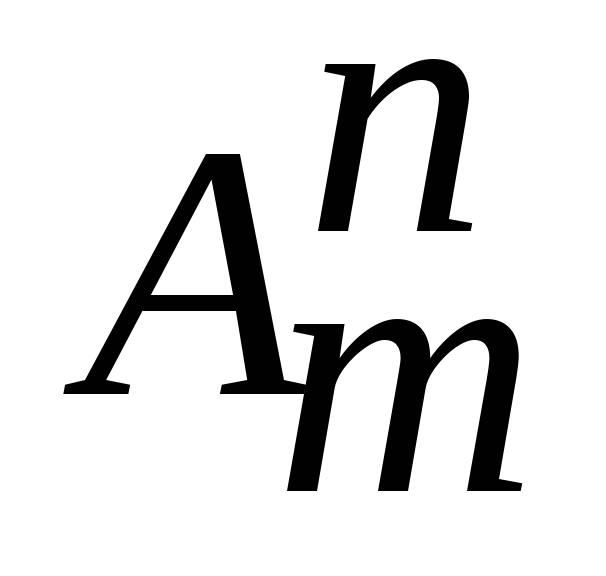называются комбинации, составленные из 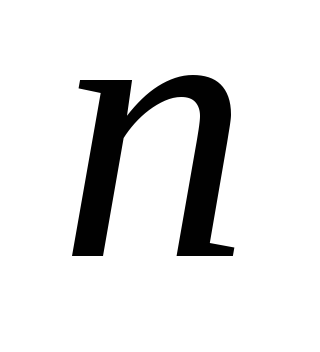– различных элементов по 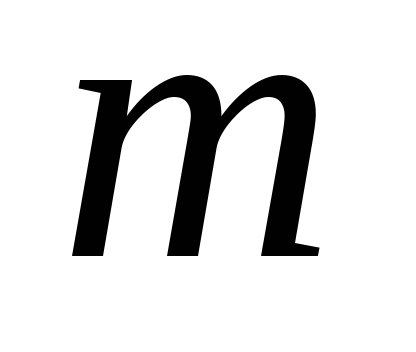– элементам, которые отличаются либо составом элементов, либо их порядком.

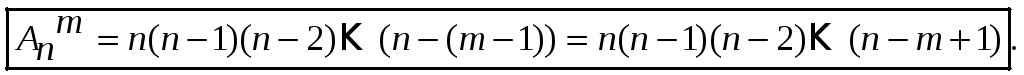
Пример. Сколько сигналов можно составить из 6 букв: A, B, C, D, E, F по 2 элемента?

AB, AC, AD, AE, AF

BA, BC, BD, BE, BF

CA, CB, CD, CE, CF

DA, DB, DC, DE, DF

EA, EB, EC, ED, EF

FA, FB, FC, FD, FE

3. Сочетаниями называют комбинации, составленные из n- различных элементов по m – элементам, которые отличаются хотя бы одним элементом.

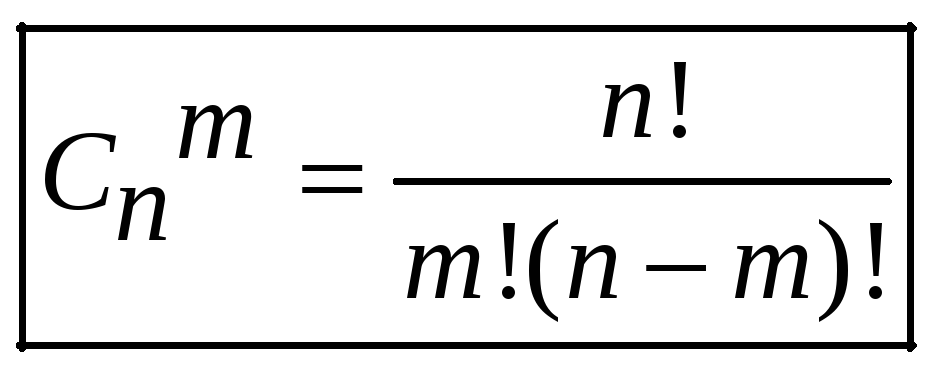
Пример. Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?

.

- связь числа размещений, перестановок и сочетаний.

Функция (интегральный закон) распределения с.В.

– является универсальной характеристикой и для непрерывных и для дискретных одномерных с.в. и описывает вероятность события :

.

Пример. Пусть случайная величина Х задана таблицей распределения (т.е. Х – дискретная случайная величина).

х	1	4	8
р	0,3	0,1	0,6

.

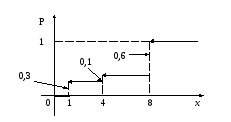
Свойства функции распределения

1. ;

2. ;

3. ;

4. - вероятность противоположного события;

5. - вероятность попадания в интервал значений.

х

6.