
- •Наблюдаемые явления (результат испытаний)
- •Алгебра событий
- •Диаграммы Эйлера-Венна
- •Доказательство теоремы о сложении вероятностей совместных событий
- •Формула полной вероятности
- •Формула вероятности гипотез
- •Формула Бернулли
- •Локальная формула Лапласа
- •Интегральная формула Лапласа
- •Случайные одномерные величины
- •Распределения вероятностей дискретной случайной величины
- •2.Распределение Пуассона
- •Основные формулы комбинаторики, используемые для определения вероятностей алгебры событий
- •Функция (интегральный закон) распределения с.В.
- •Плотность вероятности (дифференциальный закон) распределения непрерывной с.В.
- •Числовые характеристики распределения с.В.
- •Математическое (безусловное) ожидание с.В.
- •Дисперсия (безусловная) с.В.
- •5.Квантили распределения
- •Нормальное (Гауссово) распределение
- •Функция Лапласа
- •Равномерное (равновероятное, прямоугольное)
- •Показательное (экспоненциальное) распределение
- •Распределение χ2
- •Двумерные с.В. («проклятие размерности»)
- •Свойства
- •Условные математические ожидания (регрессии)
- •II. Математическая статистика
- •Построение эмпирической (статистической) функция распределения
- •Статистические оценки параметров распределения
- •Точечные оценки точности оценок (статистик) генеральных числовых характеристик
- •Математического ожидания и дисперсии
- •Доверительные интервалы оценки среднеквадратического отклонения
- •Методы оценки параметров известного распределения
- •1.Метод моментов (Пирсона)
- •2. Метод максимального правдоподобия (Фишера)
- •Парная линейная регрессия
- •Множественная линейная регрессия
- •Коэффициент детерминации регрессий
Доказательство теоремы о сложении вероятностей совместных событий
![]() - для несовместных
событий
- для несовместных
событий
![]() - для совместных
событий
- для совместных
событий
Доказательство:
Так как события А
и В считаются совместными, то событие
![]() наступит, если произойдет хотя бы одно
из трех следующих несовместных событий:
наступит, если произойдет хотя бы одно
из трех следующих несовместных событий:
![]()
Тогда
![]() (1)
(1)
Событие
![]() можно определить следующей алгеброй
событий
можно определить следующей алгеброй
событий
![]() и вероятностью
и вероятностью
![]() ,
откуда
,
откуда
![]() (2)
(2)
Аналогично для
события
![]() получим
получим
![]()
![]() (3)
(3)
Подставляя (2) и (3) в (1), будем иметь:
![]()
Замечание. Совместные события
![]() и
и
![]() могут быть зависимыми или независимыми.
Для независимых и совместных событий:
могут быть зависимыми или независимыми.
Для независимых и совместных событий:
![]() где
где
![]()
Для зависимых и совместных событий:
![]()
Пример. Вероятность попадания в
цель при стрельбе первого и второго
орудий соответственно равны:
![]() .
Найти вероятность попадания при одном
залпе (из двух орудий) хотя бы одним из
орудий. Обозначим через
.
Найти вероятность попадания при одном
залпе (из двух орудий) хотя бы одним из
орудий. Обозначим через
![]() – попадание первого орудия, а через
– попадание первого орудия, а через
![]() – попадание второго орудия.
– попадание второго орудия.
Отметим, что в данном случае
![]() и
и
![]() – независимые события, тогда
– независимые события, тогда
![]() .
Искомая вероятность будет равна
.
Искомая вероятность будет равна
![]()
Формула полной вероятности
Пусть событие
![]() может наступить при условии появления
одного из несовместных событий
может наступить при условии появления
одного из несовместных событий
![]() ,
называемых гипотезами
и образующих полную группу событий. При
этом вероятности
,
называемых гипотезами
и образующих полную группу событий. При
этом вероятности
![]() и
и
![]() будем считать
известными.
будем считать
известными.
Тогда справедлива
формула
полной вероятности
![]()
Формула полной вероятности – «удобная схема» (форма) расчета вероятности событий.
Пример 1. Имеются 2 набора деталей.
Вероятность того, что деталь первого
набора стандартна, равна 0,8, а второго
– 0,9. Найти вероятность того, что взятая
наудачу деталь из наудачу взятого набора
– стандартна. Обозначим, через
![]() событие – извлеченная деталь стандартна.
В качестве гипотез удобно принять
события
событие – извлеченная деталь стандартна.
В качестве гипотез удобно принять
события
![]() - взята деталь из первого набора,
- взята деталь из первого набора,
![]() - взята деталь из второго набора. Эти
события несовместны (берут деталь один
раз), образуют полную группу событий
(деталь берут) и, в данном случае,
равновероятны (набор выбирается
наудачу):
- взята деталь из второго набора. Эти
события несовместны (берут деталь один
раз), образуют полную группу событий
(деталь берут) и, в данном случае,
равновероятны (набор выбирается
наудачу):![]() Выбор того или иного набора – условие.
В различных наборах вероятность
извлечения стандартной детали различна:
Выбор того или иного набора – условие.
В различных наборах вероятность
извлечения стандартной детали различна:
![]() Тогда рассмотрим сумму двух событий,
каждое из которых, в свою очередь, состоит
из произведения, т.е. формулу полной
вероятности
Тогда рассмотрим сумму двух событий,
каждое из которых, в свою очередь, состоит
из произведения, т.е. формулу полной
вероятности
![]()
Пример 2. В первом наборе 20 деталей
и из них 18 - стандартны. Во втором наборе
10 деталей и из них 9 - стандартны. Из
второго набора наудачу взята деталь и
переложена в первый. Найти вероятность
того, что деталь, наудачу извлеченная
из первого набора, будет стандартна.
Введем обозначения для событий:
![]() – из первого набора извлечена стандартная
деталь,
– из первого набора извлечена стандартная
деталь,
![]() – из второго набора извлечена стандартная
деталь,
– из второго набора извлечена стандартная
деталь, ![]() – из второго набора извлечена нестандартная
деталь. Можно ли
– из второго набора извлечена нестандартная
деталь. Можно ли
![]() и
и
![]() - считать гипотезами?
- считать гипотезами?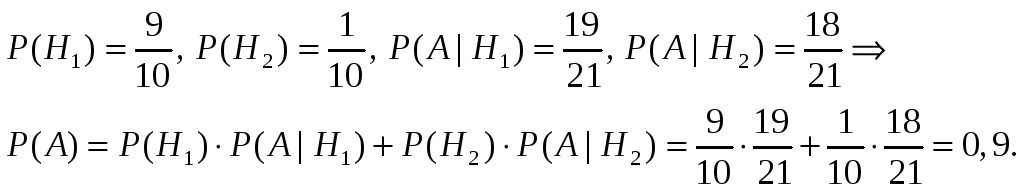
Формула вероятности гипотез
До сих пор
рассматривалась - априорная,
безусловная
вероятность гипотез
![]() .
Опытные данные (реальные события) могут
уточнить априорную характеристику
объекта анализа, определить
.
Опытные данные (реальные события) могут
уточнить априорную характеристику
объекта анализа, определить
![]() - условную
(апостериорную) вероятность гипотезы.
По формуле произведения вероятности
событий можем записать:
- условную
(апостериорную) вероятность гипотезы.
По формуле произведения вероятности
событий можем записать:
![]()
Откуда выразим
условную
апостериорную
(условие - событие
![]() произошло) вероятность
произошло) вероятность
![]()
Знаменатель раскроем по формуле полной вероятности и получим формулу вероятности гипотез (формулу Байеса, лежащую в основе известного «байесовского подхода» в уточнении гипотез):
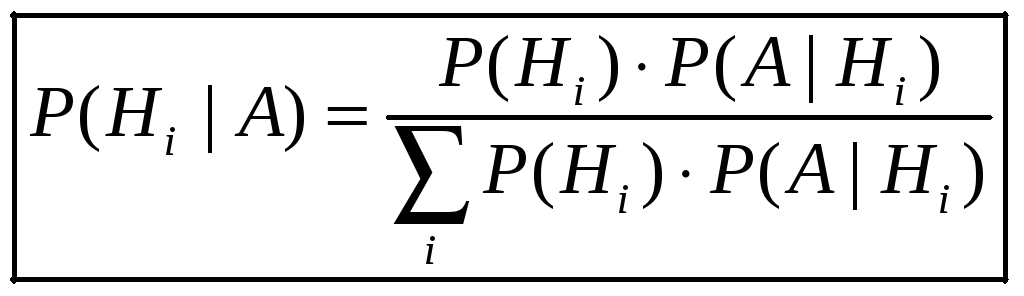 .
Например,
.
Например,
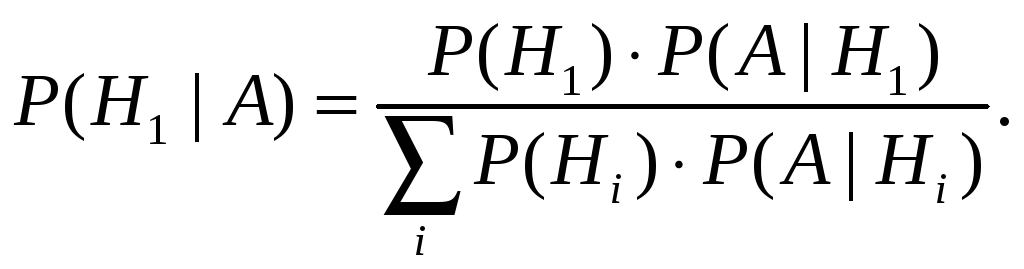
Пример. Детали, изготовленные цехом, попадают для проверки на стандартность к одному из контролеров. Вероятность того, что деталь попадет к первому контролеру, равна 0,6, а ко второму – 0,4. (Их загрузка или производительность). Вероятность того, что годная деталь будет признана стандартной первым контролером – 0,94, а вторым – 0,98 (второй имеет лучшую квалификацию). Годная деталь при проверке была признана стандартной. Найти вероятность того, что годную деталь проверил первый контролер.
Введем обозначения:![]() – деталь признана стандартной (событие
произошло); гипотезы:
– деталь признана стандартной (событие
произошло); гипотезы:
![]() - деталь проверил первый контролер,
- деталь проверил первый контролер,
![]() – деталь проверил второй контролер:
– деталь проверил второй контролер:
![]() Условные вероятности
Условные вероятности
![]()
![]() Сравним априорную и апостериорную
вероятности гипотез
Сравним априорную и апостериорную
вероятности гипотез
![]()
