Диаграммы Эйлера-Венна

Пример. В урне 30 шаров: 10 красных, 5 синих, 15 белых. Найти вероятность появления цветного шара при вынимании из урны одного шара. С появлением цветного шара свяжем или событие - вынимание красного шара, или событие вынимание синего шара.

Сумма вероятностей событий , образующих полную группу, равна 1 (условие полноты группы событий).

2.Противоположными называют два единственно возможных события, образующих полную группу.

3.Произведением двух событий и называют событие , состоящее в совместном появлении этих событий.

Пример: – деталь годна, – деталь окрашена – деталь годная и окрашенная.

Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий.

Пример: событие – появление герба при первом броске монеты, - появление герба при втором броске, - появление герба при третьем броске, – появление герба при всех трех бросках.

4.Условной вероятностью (или ) называют вероятность

события , вычисленную в предположении, что событие наступило.

Пример. В урне 3 белых шаров и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая обратно. Найти вероятность появления белого шара, при втором испытании (событие ), если при первом испытании (событие ) был извлечен черный шар. .

События и в этом примере зависимые.

- безусловная вероятность, а - условная вероятность.

5.Формула вероятности произведения двух зависимых событий.

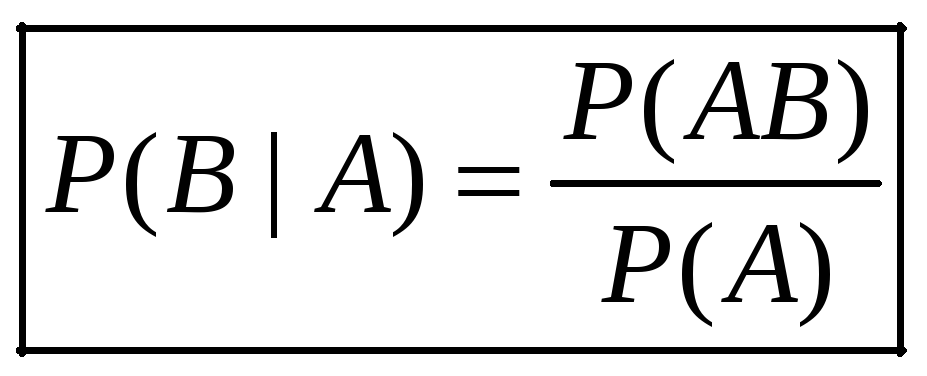и

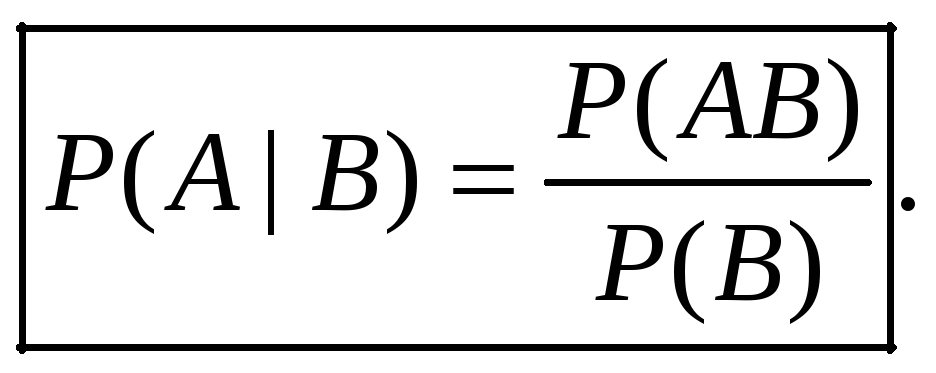
5. Формула вероятности произведения двух независимых событий:

Условие независимости: .

6.Формула вероятности произведения нескольких зависимых событий:

Пример. В урне 5 белых шаров, 4 черных и 3 синих шара. Наудачу извлекают по одному шару, не возвращая обратно. Найти вероятность того, что при первом испытании появится белый шар (событие А), при втором – черный (событие В), при третьем–синий (событие С).

Замечания: 1.Порядок, в котором расположены события, может быть выбран любым, т.е. безразлично какие события можно считать первыми, вторыми и т.д.

2.Независимость событий взаимна: если не зависит от , то и не зависит от .

7.Формула вероятности произведения нескольких независимых событий:

,

Пример 1.Вероятности появления каждого из трех событий равны: Найти вероятность появления только одного из этих событий.

Пример 2. Вероятности попадания в цель при стрельбе из трех орудий равны: Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий. Событие – попадание первым орудием, – попадание вторым орудием, А₃ – попадание третьим орудием. . Прямое событие

Обратное событие (не попал ни разу) определится следующей алгеброй

и вероятностями

Пример 3. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 попал в цель хотя бы один раз. Пусть событие – при – выстрелах стрелок попадает в цель хотя бы один раз.

Вывод: стрелок должен произвести не менее пяти выстрелов.