Теория вероятности

и математическая статистика

Лекции

Авторский текст:

проф. Семёнычев Валерий Константинович

Самара, 2007 г.

I. ТЕОРИЯ ВЕРОЯТНОСТИ

Моделирование – прогнозирование – принятие решений

Модели

Детерминированные Вероятностные Нечеткой логики

«Случайность» - непознанная закономерность

«Пирог познания»

Более сложная детерминированная модель

Более сложная вероятностная модель

Простая вероятностная модель

Простая детерминированная модель

Теория вероятностей – наука о закономерностях массовых случайных явлений (Лаплас, Пуассон, Гаусс, Бернулли, П.Л.Чебышев, А.М.Ляпунов, А.А.Марков, А.Н.Колмогоров и др.)

Теория вероятностейматематическая статистика

Курсы в ВУЗах, использующие теорию вероятности и матстатистику:

социально - экономическая статистика;

многомерные статистические методы;

эконометрика; эконометрическое моделирование;

методы социально-экономического прогнозирования;

страхование и актуарные расчеты;

теория риска и моделирования рисковых ситуаций;

маркетинг; теория массового обслуживания;

технический и фундаментальный анализ,

теория планирования эксперимента; теория надежности; теория информации (статистическая радиотехника), статистическая физика; выборочный контроль качества и др.

Предмет теории вероятностей – явления, события, случайные величины (одномерные, многомерные)

Наблюдаемые явления (результат испытаний)

Достоверные Невозможные Случайные

Условия: t=20⁰ C, P- норм. Условия t=20⁰ C, Испытание -

Р – норм бросание

монеты

Вода в сосуде – жидкая Вода в сосуде – твердая (герб или цифра)

События несовместные, если появление одного из них исключает появление других событий в одном и том же испытании.

События образуют полную группу событий, если в результате испытаний появится хотя бы одно из них.

Испытание. Бросание монеты: – герб, – цифра;

Испытание. Выстрел: - попадание, – промах (противоположное событие). и - образуют полную группу событий при одном выстреле.

Испытание. Покупают 23 лотерейных билета: событие А – выигрыш выпал на первый билет, отсутствие выигрыша на втором; событие B – выигрыш не на первом, а на втором билете; событие С – выигрыш обоих билетов; событие D – выигрыш не выпал ни на один билет.

Данные события образуют полную группу событий, если проверяются два билета. А при проверке трех билетов, что образует полную группу событий?

Испытание - игральная кость: событие A – появление числа 1, событие B 2, событие C 3, D 4, E 5, F 6. События равновероятны? (если…).

Вероятность – мера объективной возможности появления события

Классическое определение вероятности:

,

где – число исходов испытания, которое благоприятствует появлению события , – общее число исходов испытания.

Свойства вероятности:

1. Вероятность достоверного события равна 1:

2. Вероятность невозможного события равна 0:

3. Вероятность случайного события есть положительное число, заключенное между 0 и 1:,

«Судебная машина» Лапласа. Парадокс кавалера де Грие. Аксиоматика Колмогорова.

Теоретико-множественный подход к определению вероятности

- некоторое пространство элементарных событий, в котором с исходами испытаний связывают точки пространства. Каждому ставят в соответствие .

Пример. Для игральной кости: Событие – подмножество пространства элементарных событий - появление четного числа (событие):

Недостатки классического определения вероятности

1.Неприменимость при бесконечном числе исходов

Выход находят путем введения геометрической вероятности: как отношение мер длин, площадей. Примеры: рулетка, попадание точки в отрезок длиной на отрезке длиной : .

2. Априори трудно представить результат испытаний в виде совокупности элементарных событий, еще труднее указать основание, позволяющее считать элементарные события равновозможными.

Тогда вводят статистическую (апостериорную) вероятность ,

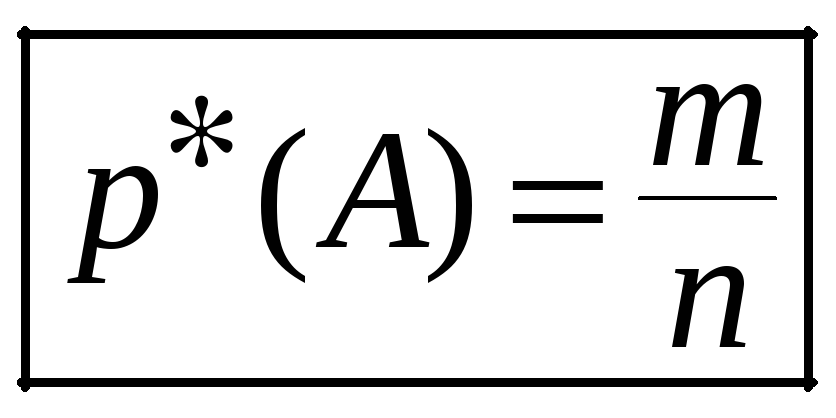– число исходов, в которых событие появилось, – общее число исходов

Алгебра событий

1.Суммой двух событий и называют событие , состоящее в появлении или , или , или обоих (если они совместны).

Пример. Для двух выстрелов сумма событий: – попадание при первом выстреле, попадание при втором выстреле, – попадание при обоих выстрелах, т.е.

Суммой нескольких событий называют событие, заключающееся в появлении хотя бы одного из них. .

При несовместных событиях: