
- •1 Курс, 1 семестр.
- •1.Свойства степени с произвольным показателем.
- •2. Определение логарифма числа и его свойства. Натуральные и десятичные логарифмы.
- •Свойства логарифмов.
- •3.Тригонометрические функции числового аргумента(определения, табличные значения).
- •Табличные значения тригонометрических функций
- •1.Арккосинус
- •Табличные значения арккосинуса
- •2.Арксинус
- •Табличные значения арксинуса
- •3.Арктангенс
- •Табличные значения арктангенса
- •4.Арккотангенс
- •5.2.Формулы суммы и разности аргументов.
- •5.3.Формулы двойного аргумента.
- •5.4.Вывод формул понижения степени.
5.4.Вывод формул понижения степени.
cos
1 cos2
cos2
1 cos2
cos2
(4)
1

Выразим
 - Формула
понижения степени
- Формула
понижения степени
cos
cos2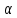 =
=
1 cos2
cos2
1 cos2
cos2
1 cos2
cos2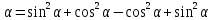
1 cos2
cos2
(5)

sin
Из
формул с 1 по 3 заменим
 ,
получим 6 формулу
,
получим 6 формулу
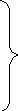
(6)
sin
Формулы половинных углов
(7)
cos
(8)
tg
5.5.Формулы суммы и разности
тригонометрических функций.
Формулы сложения тригонометрических функций позволяют преобразовывать сумму и разность функций в произведение этих функций.
sin
cos
sin
cos
5.6.Формулы приведения.
Значения тригонометрических функций острых углов вычисляют по таблице, либо по модели числовая окружность.
Значения функций любых углов можно вычислить с помощью формул приведения к острому углу. Формул приведения много, поэтому лучше запомнить правило написаний этих формул, а не сами формулы.
ПРАВИЛО НАПИСАНИЯ ФОРМУЛ ПРИВЕДЕНИЯ:
1)
Если под знаком тригонометрической
функции содержится ( ,
или (
,
или ( ,
то наименование функции нужно изменить
на родственное (sin
cos
; tg
ctg)
,
то наименование функции нужно изменить
на родственное (sin
cos
; tg
ctg)
2)
Если под знаком тригонометрической
функции содержится ( то наименование тригонометрической
функции менять не нужно.
то наименование тригонометрической
функции менять не нужно.
3)Перед полученной функцией от аргумента t нужно поставить тот знак, которая имела бы преобразуемая функция при условии, что
0<t< (0
(0 <
< <90
<90
1)
sin ( 17) tg (
17) tg (
2)
sin ( 18) tg (
18) tg (
3)
sin (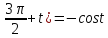 19) tg (
19) tg (
4)
sin
 20) tg
20) tg

5)
sin ( 21) tg (
21) tg (
6)
sin
 22) tg
22) tg

7)
sin
 23) tg
23) tg

8)
sin
 24) tg
24) tg

9)
cos ( 25) ctg (
25) ctg (
10)
cos ( 26) ctg (
26) ctg (
11)
cos ( 27) ctg (
27) ctg (
12)
cos
 28) ctg
28) ctg

13)
cos ( 29) ctg (
29) ctg (
14)
cos
 30) ctg
30) ctg

15)
cos
 31) ctg
31) ctg

16)
cos
 32) ctg
32) ctg

6.Решение уравнения sinx=a.
(вывод формул корней уравнения sint=a)
Если
 то уравнение sin
=a
имеет корни, если
то уравнение sin
=a
имеет корни, если
 то уравнение корней не имеет. Например:
то уравнение корней не имеет. Например:
sint = 2
2 нет корней
нет корней
sint = -1,8
|-1,8|=1,8 нет корней
нет корней
Вывод формул корней


 0;
0;
t=
arcsina+ k
k
Вывод:
Уравнение sint a
имеет две серии решений:
(1)
a
имеет две серии решений:
(1)
 arcsina
arcsina
(2)
Эти две формулы объединим в одну:
t k
k
(1)
t

при любом k
(2)
t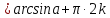
t
=

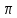 k
k
Формула корней уравнения sin t=a

Свойство:
 (1) формула
(1) формула
 (2) формула
(2) формула
Три частных случая:
1)
sint
 t
t
2)
sint t
t
3)
sin
 t
t
Например, Решить уравнение
sint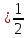
t
t
7.Решение уравнения cosx=a
(Вывод формул корней уравнения cost=a)
Решить тригонометрическое уравнение cost=a, значит найти все числа t на окружности cos, которых равен числу a.
y


a
x
|a| 1
1
Если
|a| то тригонометрическое уравнение cos
t=a
имеет корни.
то тригонометрическое уравнение cos
t=a
имеет корни.
Если
|a| то тригонометрическое уравнение cos
t=a
не имеет решений.
то тригонометрическое уравнение cos
t=a
не имеет решений.
cos
t 1,5
1,5 нет корней
нет корней
cos
t |
|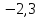 |
| нет корней
нет корней
y Вывод формул корней


(k
x
 1
1

Вывод: Уравнение cost=a имеет две серии решений:
t= k
k
t= (k
(k ,
которые можно объединить в одну формулу
,
которые можно объединить в одну формулу

Формула корней уравнения cost=a

Свойство:
Но в трёх частных случаев предпочитают пользоваться не формулой корней, а более простыми соотношениями:
1)
cos t
 t
t
2)
cos t t
t
3)
cos
t t
t
Например, Решить уравнение
cos
t
|a|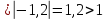 нет корней
нет корней
8.Решение уравнения tgx=a.
(Вывод формулы корней уравнения tgt=a),
y
где a-любое
действительное число на линии tg.
tg
a +
t=arctga
x


Формула
корней уравнения tgt a:
a:

Свойство:
Частных случаев нет!
Например, Решить уравнение:
tgt=1,5
t=arctg1,5
9.Решение уравнения ctg=a.
(Вывод формулы корней уравнения ctgt=a),
Где
a-любое
действительное число на линии ctg
y
ctgt 0 a ctgt
arcctga
x
arcctga+
t
Формула корней уравнения ctgt=a
Свойство:
arcctg(-a)
Например, Решить уравнение:
ctgt
t
tgt


0

 ctgt
ctgt
 1
1
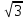 ctgt
ctgt







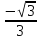

 0;2
0;2
0



x











|
|
Страница |
|
|
|
|
