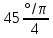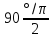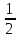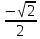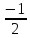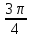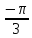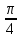Табличные значения тригонометрических функций

sint	0				1	0	-1	0
cost	1				0	-1	0	1
tgt	0		1		Не сущ.	0	Не сущ.	0
ctgt	0		1		0	Не сущ.	0	Не сущ.

4.Обратные тригонометрические функции (Определение, свойства, табличные значения)

1.Арккосинус

Определение: Арккосинусом числа a (arccos a), где a , называется такое число t на окружности (или угол) t, косинус которого равен числу a

cos t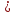 a

arccosa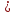t

0

Свойство арккосинуса:

arccos(-a)-arccosa

Функция не является ни четной, ни нечётной

Табличные значения арккосинуса

	-1				0				1
t=arccosa									0

2.Арксинус

Определение: Арксинусом числа a(arcsina), где -1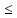a1, называется такое число t на окружности (или угол) tсинус которого равен числу a

sin ta

arcsina=t

Свойство арксинуса:

arcsin(-a)=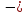arcsina

Функция не чётная

	-1				0				1
t=arcsina					0

Табличные значения арксинуса

3.Арктангенс

Определение: Арктангенсом числа a (arctga), где a-любое действительное число на линии tg, называется такое число t на окружности из интервала, тангенс которого равен числу a

tg ta

arctga=t

a-любое

Свойство арктангенса:

arctg(-a)=arctga

Функция не чётная