10.1 Эллипсоид
Поверхность, задаваемая в ортонормированной системе координат каноническим уравнением вида
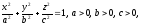
называется эллипсоидом.
Свойства эллипсоида
1.
Эллипсоид – ограниченная поверхность,
поскольку из его канонического уравнения
следует, что
.
2. Эллипсоид обладает:
- центральной симметрией относительно начала координат;
- осевой симметрией относительно координатных осей;
- плоскостной симметрией относительно координатных плоскостей.
3. В
сечении эллипсоида плоскостью,
ортогональной любой из осей координат,
получается эллипс (см. рис.).
z
y
x
10.2 Эллиптический параболоид
Поверхность, задаваемая в ортонормированной системе координат каноническим уравнением вида
называется эллиптическим параболоидом.
Свойства эллиптического параболоида
1.
Эллиптический параболоид – неограниченная
поверхность, поскольку из его канонического
уравнения следует, что
и принимает сколь угодно большие
значения.
z
x
y
2. Эллиптический параболоид обладает
-
осевой симметрией относительно оси
;
-
плоскостной симметрией относительно
координатных плоскостей
и
.
3.В
сечении эллиптического параболоида
плоскостью, ортогональной оси
,
получается эллипс, а плоскостями,
ортогональными осям
или
– парабола.
10.3 Гиперболический параболоид
Поверхность, задаваемая в ортонормированной системе координат каноническим уравнением вида
,
называется гиперболическим параболоидом.
Свойства гиперболического параболоида
1.
Гиперболический параболоид –
неограниченная поверхность, поскольку
из его канонического уравнения следует,
что
– любое.
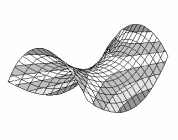
z
x
y
2. Гиперболический параболоид обладает
-
осевой симметрией относительно оси
;
-
плоскостной симметрией относительно
координатных плоскостей
и
.
3.В
сечении гиперболического параболоида
плоскостью, ортогональной оси координат
,
получается гипербола, а плоскостями,
ортогональными осям
или
,
– парабола.
10.4 Однополостный гиперболоид
Поверхность, задаваемая в некоторой ортонормированной системе координат каноническим уравнением вида
называется однополостным гиперболоидом.
Свойства однополостного гиперболоида
1.
Однополостный гиперболоид – неограниченная
поверхность, поскольку из его канонического
уравнения следует, что
.
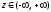z
x y
2. Однополостный гиперболоид обладает (см. рис.)
- центральной симметрией относительно начала координат;
- осевой симметрией относительно всех координатных осей;
- плоскостной симметрией относительно всех координатных плоскостей.
3.
В сечении однополостного гиперболоида
плоскостью, ортогональной оси координат
,
получается эллипс, а плоскостями,
ортогональными осям
или
– гипербола.