9.2 Эллипс и его свойства

Кривая, уравнение которой в некоторой ортонормированной системе координат имеет вид , называется эллипсом.

Число называется эксцентриситетом эллипса.

Точки называются фокусами эллипса.

Прямые называются директрисами эллипса.

Число называется фокальным параметром эллипса.

Свойства эллипса:

Эллипс – ограниченная кривая: и что следует из записи канонического уравнения в форме ;

Эллипс L обладает осевой симметрией относительно осей Ox и Oy, а также центральной симметрией относительно начала координат.

Свойства эллипса иллюстрирует рисунок:

Y b D2 B A -a F2 O F1 a

Фокальное свойство эллипса: эллипс есть геометрическое место точек, сумма расстояний от которых до двух фокусов постоянна и равна .

Уравнение эллипса в полярных координатах:

y .

ρ A

F  O x

9.3 Гипербола и ее свойства

Кривая, уравнение которой в некоторой ортонормированной системе координат имеет вид называется гиперболой.

Число называется эксцентриситетом гиперболы.

Точки называются фокусами гиперболы.

Прямые называются директрисами гиперболы.

Число называется фокальным параметром гиперболы.

Cвойства гиперболы:

1. Гипербола – неограниченная кривая, существующая для что следует из записи канонического уравнения в форме (см. рис.).

2. Гипербола обладает осевой симметрией относительно осей Ox и Oy, а также центральной симметрией относительно начала координат.

3. Гипербола обладает асимптотами вида .

Фокальное свойство гиперболы: гипербола есть геометрическое место точек, абсолютная величина разности расстояний от которых до двух фокусов постоянна и равна .

Уравнение гиперболы в полярной системе координат

.

9.4 Парабола и ее свойства

Кривая, уравнение которой в некоторой ортонормированной системе координат имеет вид , называется параболой.

Точка называется фокусом параболы.

Прямая называется директрисой параболы.

Число p называется фокальным параметром параболы.

Свойства параболы иллюстрирует рисунок.

D y

O F x

Свойства параболы:

1. Парабола – неограниченная кривая, существующая

2. Парабола обладает осевой симметрией относительно оси Ox.

3. Для параболы имеет место монотонное возрастание абсолютной величины ординаты при возрастании абсциссы, причем в нуле касательная к параболе вертикальна.

Замечание о свойствах параболы

Каноническое уравнение, изучаемой в курсе элементарной математики параболы вида , получается путем взаимного переименования координатных переменных.

Свойство параболы: парабола есть геометрическое место точек, отношение расстояния от которых до данной точки (фокуса) к расстоянию до данной прямой (директрисы) постоянно и равно единице.

Уравнение параболы в полярной системе координат

y

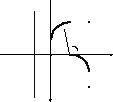
A

ρ φ

D O F x

.

СВОЙСТВА ПОВЕРХНОСТЕЙ

ВТОРОГО ПОРЯДКА

Лекция 10

Описание свойств невырожденных поверхностей второго порядка будет выполнено в ортонормированной системе координат .

В общем случае в сечении поверхности второго порядка плоскостью получается кривая второго порядка. Для описания основных свойств невырожденных поверхностей второго порядка достаточно рассмотреть сечения, параллельные координатным плоскостям.