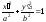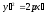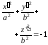8.1. Линии второго порядка на плоскости

Пусть на плоскости дана ортонормированная система координат и некоторая линия L.

Определение. Линия L называется алгебраической линией второго порядка, если ее уравнение в данной системе координат может иметь вид

(8.1)

где числа A, B и C не равны нулю одновременно, а x и y - координаты радиуса-вектора точки, принадлежащей L.

Поскольку коэффициенты уравнения (8.1) зависят от выбора системы координат, при исследовании свойств линий второго порядка целесообразно перейти к другой ортонормированной системе координат , в которой запись уравнения линии оказывается наиболее простой.

Обозначим , тогда будет справедлива теорема.

Теорема 8.1 Для любой линии второго порядка существует ортонормированная система координат, в которой уравнение этой линии имеет (при ) один из следующих девяти (называемых каноническими) видов:

Тип линии Вид линии	Эллиптический	Гиперболический	Параболический
Пустые множества
Изолированные точки
Совпадающие прямые
Несовпадающие прямые
Кривые	Эллипс	Гипербола	Парабола

Замечание 1. При замене системы координат порядок алгебраической линии не меняется.

Замечание 2. Никакой заменой общей декартовой системы координат нельзя переместить линию второго порядка, находящуюся в одной из клеток таблицы в другую клетку.

Замечание 3. Пустое множество эллиптического типа иногда называют мнимым эллипсом, а пустое множество параболического типа – парой мнимых параллельных прямых.

8.2 Поверхности второго порядка в пространстве

Пусть дана ортонормированная система координат в пространстве.

Определение. Поверхность S называется алгебраической поверхностью второго порядка, если ее уравнение в данной системе координат имеет вид

(8.2)

где числа не равны нулю одновременно, а x, y и z - координаты радиуса-вектора точки, принадлежащей S.

Как и в плоском случае, коэффициенты уравнения (8.2) зависят от выбора системы координат, поэтому при исследовании свойств поверхностей второго порядка целесообразно предварительно перейти в ту систему координат, для которой уравнение поверхности оказывается наиболее простым.

Теорема 8.2 Для каждой поверхности второго порядка существует ортонормированная система координат , в которой уравнение этой поверхности имеет один из следующих семнадцати канонических видов: