
Лабораторные работы / Вариант № 58
.docБАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ФАКУЛЬТЕТ ВЕЧЕРНЕ-ЗАОЧНЫЙ
КАФЕДРА УПРАВЛЕНИЯ И ИНФОРМАТИКИ ТЕХНИЧЕСКИХ СИСТЕМ
Практическая работа № 1
Анализ системы автоматического управления.
Выполнил: ст.гр. УИТ-51в
Петрова Е.В.
Проверил: преподаватель
Свиридова Е.В.__________
«_____»___________2005г
Балаково 2005
Цель работы: изучить преобразование структурной схемы САУ.
Вариант № 58
Дано:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
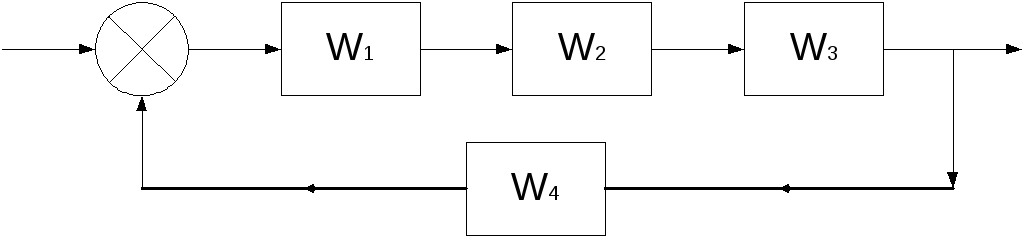
Исходная схема

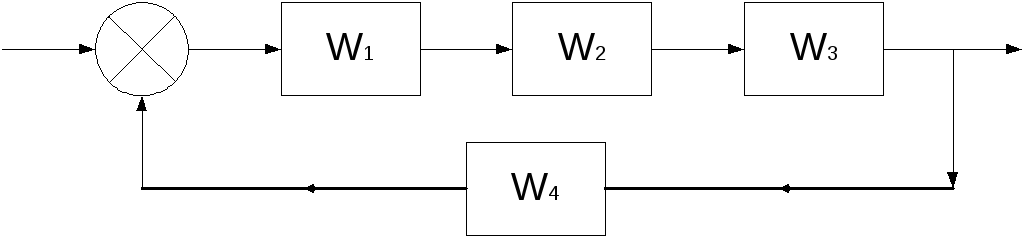
1. Преобразуем
данную структурную схему и определим
общую передаточную функцию:
![]()

Найдем передаточную функцию разомкнутой системы.
![]()
![]()
![]()
2. Исследуем схему на устойчивость по критериям:
-
метод Ляпунова.
Этот метод заключается в том, чтобы вещественные корни дифференциального уравнения были отрицательны, а комплексные корни имели отрицательную реальную часть.
![]()
![]()
![]()
![]()
Т.к. вещественный корень дифференциального уравнения отрицательный, то система устойчивая.
-
алгебраический метод Гурвица
Для устойчивости системы необходимо и достаточно, чтобы все миноры определителя Гурвица были положительны.
![]()
![]() ,
, ![]()
Все коэффициенты характеристического уравнения положительны, следовательно необходимое условие устойчивости выполняется.
По коэффициентам уравнения составим определитель Гурвица.
![]()
Определяем значение миноров.
![]()
![]()
![]()
Т.к. все миноры определителя Гурвица положительны, следовательно, система устойчива.
-
алгебраический метод Рауса
Для устойчивости системы необходимо и достаточно, чтобы все коэффициенты первой графы таблицы Рауса были положительны.
![]()
Правила составления таблицы Рауса:
-
В первой строке таблицы Рауса записываются, соответственно, коэффициенты
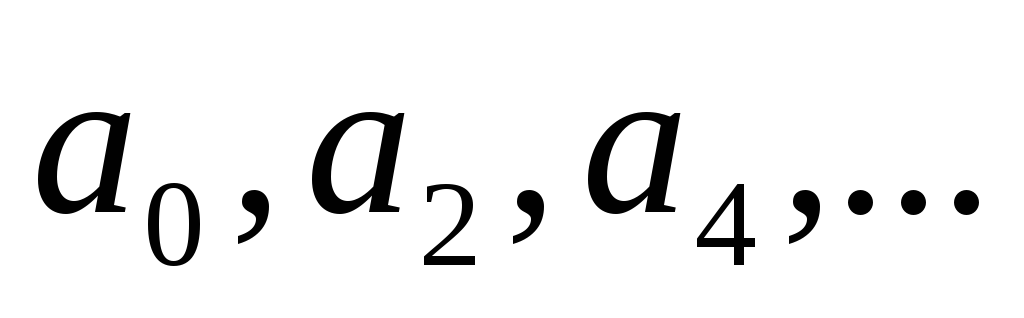
-
Во второй строке таблицы Рауса записываются, соответственно, коэффициенты

-
Коэффициенты третей сроки, вычисляются по формуле
![]()
![]()
………………….……………….
где
![]()
![]()
4. Коэффициенты четвертой сроки, вычисляются по формуле
![]()
![]()
![]()
……………….
где
![]()
5. Коэффициенты n-ой сроки, вычисляются по формуле
![]()
![]() ,
где i
– номер столбца, j
– номер строки.
,
где i
– номер столбца, j
– номер строки.
Составим таблицу:
|
№ № срок |
1 |
2 |
|
1 |
0,047 |
0 |
|
2 |
1 |
0 |
Все коэффициенты первого столбца положительны, следовательно, система устойчива.
-
метод Льенара-Шипара
Для того, чтобы система была устойчива, необходимо и достаточно, чтобы все определители Гурвица с четными и нечетными индексами были положительны.
Т.к. данное условие выполняется, то система устойчива.
-
метод Шур-Кона
Алгебраический критерий Шур-Кона позволяет судить о расположении корней на плоскости Z, по характеристическому уравнению замкнутой системы. Если коэффициенты уравнения удовлетворяют условию:
∆k<0,
∆k>0, где k – определитель Шур-Кона.
![]()
Произведем Z-преобразование данной передаточной функции, при Т=0,03 (период дискретизации) получим
![]()
![]()
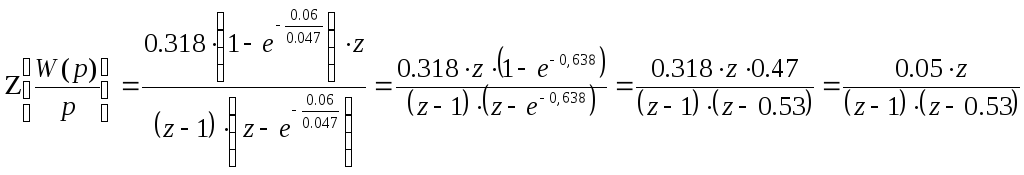
![]()
Характеристическое
уравнение Z – преобразованной
функции имеет вид: ![]()
![]()
т.к. нечетный определитель Шур-Кона меньше ноля, то система устойчива.
-
метод выделения области устойчивых и неустойчивых состояний с помощью Д-разбиения.
![]()
Характеристическое уравнение имеет вид: 0,13р+1=0
W(jω)=0,13jω+1
![]()
![]()
Составим
определитель:
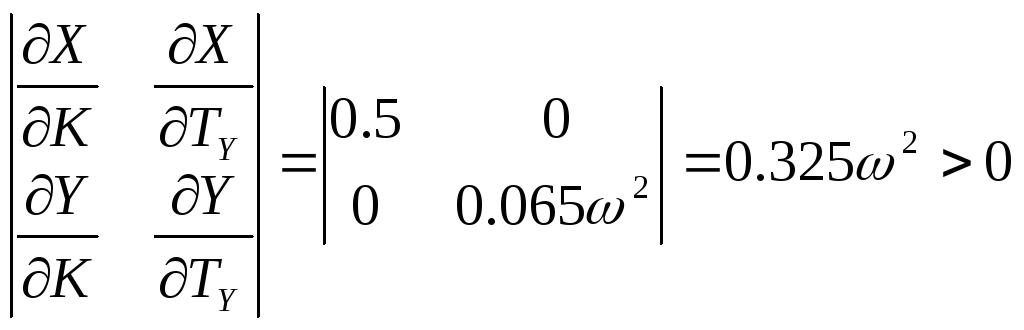
При изменении
частоты в пределах от 0 до
![]() определитель будет положительным,
поэтому при движении по полученной
кривой сверху вниз надо штриховать
область лежащую слева от кривой.
определитель будет положительным,
поэтому при движении по полученной
кривой сверху вниз надо штриховать
область лежащую слева от кривой.

















Область
![]() является областью устойчивости системы.
является областью устойчивости системы.
-
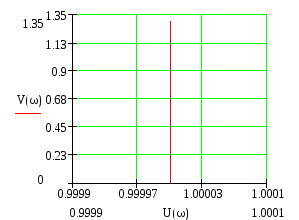
частотный метод устойчивости по Михайлову
Критерий: для устойчивой системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от нуля до бесконечности повернулся против часовой стрелки, начиная с вещественной оси, на число квадрантов равное порядку характеристического уравнения, последовательно проходя эти квадранты.
Запишем передаточную функцию в следующем виде:
![]()
Характеристическое
уравнение данной передаточной функции
имеет вид: ![]()
Введем
замену
![]()
![]()
Выделим
мнимую и действительную части:
![]()
Построим годограф:

Мы видим, что система устойчива, т.к. выполняется условие последовательного прохождения квадрантов против часовой стрелки.
-
частотный метод устойчивости по Найквисту
Критерий: если
система устойчива в разомкнутом
состоянии, то для устойчивости замкнутой
системы необходимо и достаточно, чтобы
слово АФЧ разомкнутой системы для
частоты ω, изменяющейся от 0 до
![]() ,
не охватывало точку с координатой (-1;
jω).
,
не охватывало точку с координатой (-1;
jω).
![]()
Домножим функцию на комплексно сопрежонное, получим
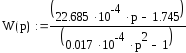
Введем
замену
![]()

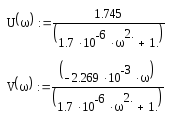
Выделим мнимую и действительную части
Построим годограф.
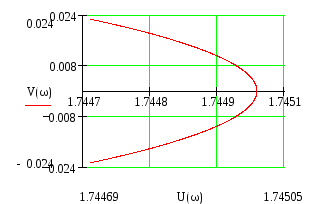
Система устойчива, т.к. условие выполняется.
3. Построим переходный процесс системы. Определим время регулирования и перерегулирования.
![]()
Функция, определяющая изменение выходной величины системы при подаче на ее вход единичного ступенчатого воздействия и при нулевых начальных условиях называется переходной функцией системы и обозначается: h(t).
Найдем переходную функцию с помощью преобразований Лапласа.
![]()



По виду переходной характеристики можно также сказать, что данная система устойчива.
По переходному процессу определим прямые оценки качества.
а) Время
переходного процесса – это время за
которое регулируемая величина входит
в пятипроцентную трубку. ![]()
б) Время
первого согласования – это время за
которое регулируемая величина первый
раз достигает установившееся значение. ![]()
в) Перерегулирование – определяем максимальную динамическую ошибку.
![]()
![]() ,
, ![]() ,
,
то
![]()
Для
обеспечения запаса устойчивости примем
![]()
4. Постоим ЛАЧХ неизменяемой части.
Для построения ЛАЧХ разомкнем систему, то получим
![]() ,
,
тогда ![]()
Найдем мнимую и действительную части:
![]()
![]()
![]()
Построим график ЛАЧХ.
К=1,7453 ![]() ,
,
![]()
![]()
5. Построим ЖЛАЧХ
- метод Солодовникова
По
переходному процессу мы получили
![]() и
и
![]() ,
тогда
,
тогда
![]()
![]()
![]()
Графики смотри приложение.
- метод запретной зоны
![]()
Произведем Z-преобразование данной передаточной функции, при Т=0,03 (период дискретизации) получим
![]()
![]()

![]()
Перейдем к псевдо частоте:
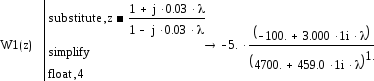
![]()
К=0,106 ![]() ,
,
![]()
![]()
![]()
![]()
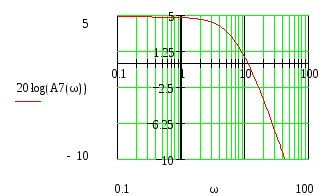
Построим график ЛАЧХ:

Определим
среднечастотную область, с верхней
границей
![]() (дБ)
и с нижней границей
(дБ)
и с нижней границей
![]() (дБ). Примем М=1,3. Наклон ЖЛАЧХ в
среднечастотной области равен –20
дБ/дек. Наклон ЖЛАЧХ в высокочастотной
области должен быть близким к наклону
исходной ЛАЧХ, в нашем случае он совпадает.
(дБ). Примем М=1,3. Наклон ЖЛАЧХ в
среднечастотной области равен –20
дБ/дек. Наклон ЖЛАЧХ в высокочастотной
области должен быть близким к наклону
исходной ЛАЧХ, в нашем случае он совпадает.
7. Коррекция
- последовательная коррекция

![]()
![]()
Из полученного выражения видно, что коррекция не требуется, нужно лишь увеличить коэффициент усиления.
По виду ЛАЧХ корректирующего устройства находим схему (№ 49):

![]() ,
,
где
![]()
![]()
Примем
![]() ,
тогда
,
тогда
![]()
![]()
Получаем схему параллельного включения:
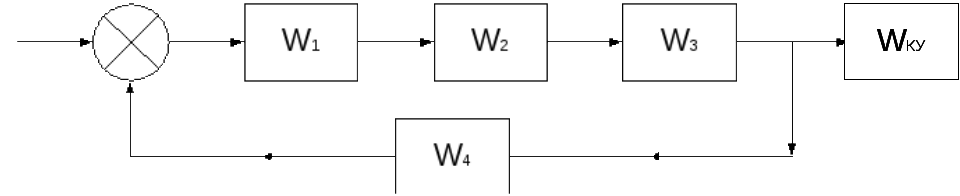
- параллельная коррекция
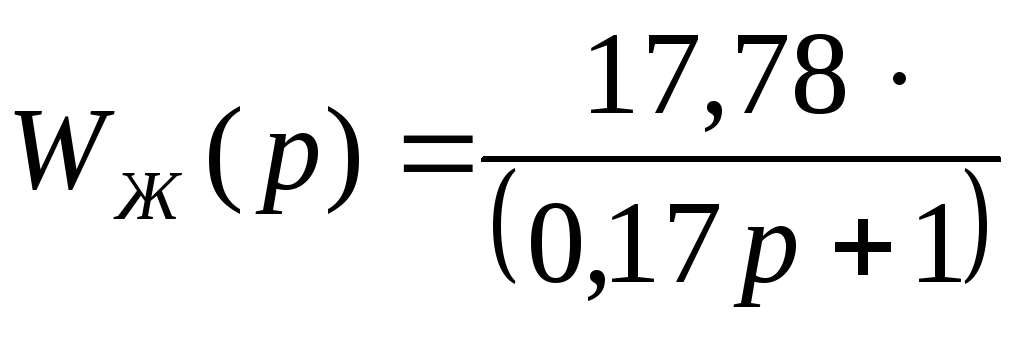
![]()
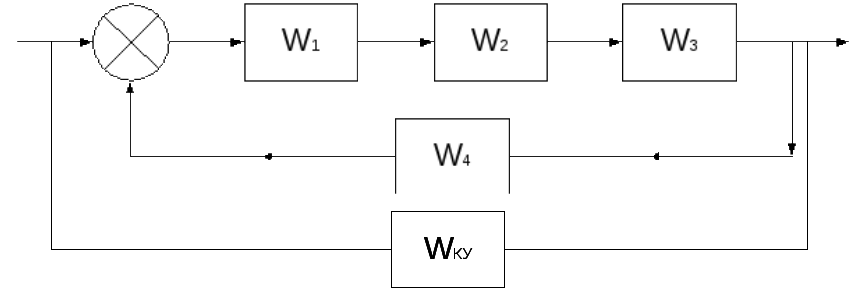
- параллельно-последовательная коррекция
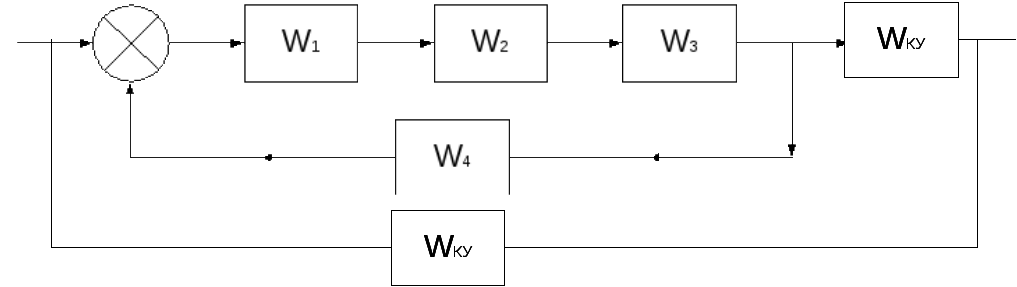

 столб
столб