52. Решение статистических игр при неизвестных вероятностях состояний природы. Критерий Вальда и Гурвица.

Игроку А могут быть известны вероятности, с которыми природа реализует свои состояния, но он может их не знать.

Если объективные оценки состояния природы получить невозможно, но вероятности природы могут быть оценены субъективно на основе принципа недостаточного основания Лапласа, согласно которому все состояния природы полагаются равновероятностными, т.е.

q₁=q₂=…….=q_n= и оптимальной считают стратегию А_i, обеспечивающую максимальное среднее значение выигрыша

=

. Матрица рисков Сэвиджа

Построение матрицы рисков. Риском r_ij игрока А, когда он пользуется своей чистой стратегией А_i при состоянии природы П_j наз. разность м/у min-ым выигрышем, кот. он м. бы получить, если бы точно знал, что природой б. реализовано именно состояние П_j и тем выигрышем, кот он реально получит, используя стратегию A_i, не зная какое же состояние реализует природа.

r_ij=_j-a_ij>=0 _j=maxa_ij, i=1,m

i j=1,

Где В_j=max a_ij – максимальный элемент j-го столбца платежной матрицы. Элементы матрицы рисков, соответствующие стратегиям А_i и П_j характеризуют общую благоприятность или не благоприятность для игрока А отдельных состояний природы.

. Критерии Байеса, Гурвица, Вальда и Сэвиджа.

3. Критерий, основанный на известных вероятностях условий. Пусть известны вероятности q_j состояний природы П, j=1;n.Тогда пользуемся критерием Байеса, в соответствии с кот. Оптимальная считается чистая стратегия A, при которой максимизируется средний выигрыш

=i=1;n

игрока А, т.е. определяется величина:

=

4. Махмin-ный критерий Вальда.

Согласно этому критерию рекомендуется применять маxмin-ную стратегию, она находится из условия

α=

и совпадает с нижней чистой ценой игры.

5. Критерий максимума - оптимистический критерий. Считается, что природа наиболее благоприятна для игрока А и оптимальная стратегия находится из условия

m=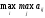

6. Критерий Гурвица – рекомендует выбирать стратегии, определ. по формуле:

S=)}i=1;m j=1;n a_ij-элемент платежной матрицы [0;1]

Критерий поддерживается некоторой промежуточной позицией, кот. учитывает возможность как наихудшего, так и наилучшего поведения природы. При =1 этот критерий превращается в критерий Вальда. При =0 получается критерий максимума, выбираем из опыта или субъективных соображений.

7. Критерий Сэвиджа. Суть состоит в выборе такой стратегии, кот. не позволяет допустить чрезмерно высокие потери. Этот критерий также как и критерий Вальда является критерием крайнего пессимизма, но пессимизм здесь понимается иначе. Тут рекомендуется всячески избегать большого риска. Согласно этому критерию выбирается стратегия, при которой в наихудших условиях величина риска принимает наименьшее значение, т. е.

r= r-элемент матрицы рисков.

.Сетевое планирование. Основные понятия. Правила построения сетевых графиков.

Ранний срок t_р(i) свершения события i – самый ранний момент времени, к которому завершаются все предшествующие этому событию работы.

Поздний срок t_п (i) свершения события i – самый поздний момент времени, после которого остается столько времени, сколько необходимо для завершения всех работ.

Резерв времени события R(i) – разность между поздним и ранним сроками свершения события.

Ранний срок начала работы(i,j) равен t_р(i).

Ранний срок окончания работы(i,j) равен сумме раннего срока свершения начального события работы и ее продолжительности.

Поздний срок окончания работы равен позднему сроку свершения ее конечного события.

Поздний срок начала работы – разность между позднм сроком свершения ее конечного события и продолжительностью.

Правила построения сетевого графика.

Имеется сеть дорог. А – пункт отправления, В – пункт назначения, между ними есть промежуточные пункты, и некот. из них соединены между собой. Над каждым участником сети указаны расстояния между пунктами или стоимость доставки грузов. Найти кратчайший путь.(График)….

Решение:

1. Разбиваем все пункты транспортной сети на группы. Вычеркиваем все стрелки, выходящие из пункта 1. Пункты, в кот. не входит ни одна стрелка объединяем в группы.

2. Условная оптимизация. Двигаясь от В в А, для каждого из пунктов определим кратчайший путь от этого пункта до В и записываем длину этого пути рядом с соответствующим пунктом.

3. Безусловная оптимизация. Двигаясь от А в В, по найденным значениям определим пункты кратчайшего пути.

При выборе решения на каждом шаге необходимо учитывать интересы всей задачи в целом, а не только данного шага.

Основные параметры, которые можно определить для каждой из работ сетевого графика (ранние и поздние сроки начала и окончания работ, резервы времени работ).

Основным временным параметром сетевого графика явл. Продолжительность критического пути. Расчёт его вкл. 2 этапа:

1. Вычисления начинают с исходного события и для каждого события определяют число, представляющее ранний срок его наступления.

2. Вычисления начинают с завершающего события и продолжают, пока не будет достигнуто исходное событие. Для каждого события вычисляют поздний срок его наступления.

Ранним сроком наступления события i наз. самый ранний момент времени, к которому завершаются все предшествующие этому событию работы: tp(i) = t[L1(i)]

Поздним сроком совершения события iявл-ся самый поздний момент, после которого остаётся столько времени, сколько необходимо для завершения всех, следующих за этим событием, без превышения критического времени: tкр

tп(i) = tкр- t[L2(i)]

Для событий критического пути ранний и поздний сроки свершения совпадают, а раздность между ними – это резерв времени события

R(i) = tп(i)-tp(i)

Резервы критических событий = 0

Верхний сектор- номер событий, правый- поздний срок свершения, левый- ранний срок свершения, нижний- резерв времени.

Временные параметры работ.

Ранний срок начала работы(i,j) = раннему сроку свершения события i:

Tрн(i;j)= tp(i)

Ранний срок окончания работы = сумме раннего срока совершения начального соб-я и её продолжительности

Tp(i,j) = tp(i)+tij

Поздний срок окончания работы = поздн. сроку совершения её конечного события:

Tno(i,j) = tп(j)

Поздний срок начала работы = разности между поздним сроком совершения её конечного соб-яф и продолжительностью:

Tnн(i,j) = tп(j) – tij

Полный резерв времени работы- мах возможный запас времени, на который можно отсрочить начало работы или увеличить продолжительность уё выполнения при условии, что конечное для данной работы событие наступит не позднее своего позднего срока.

Rп(i,j) = tп(j) – tp(i) – tij

Все некритические работы имеют полный резерв времени отличный от 0.

Сетевое планирование. График Ганта.

На графике каждая работа изображается в привязке к оси времени сплошным горизонтальным отрезком, длина которого = продолжит-ти работы. Начало каждой работы= раннему сроку свершения её начального события. Пунктирный отрезок соответствует каждому резерву времени работы. Изобразив все работы проекта получим график Ганта. По нему можно определить критическое время выполнения проекта, а также работы, принадлежащие критич. пути.

Сетевое планирование. График интенсивности использования ресурсов.

Пусть заданы потребности в трудовых ресурсах для выполнения каждой работы и , известно ограничения R, имеющихся трудовых ресурсов. Выясним, сколько требуется ресурсов для выполнения работ проекта в каждый момент времени. Для этого на основе сетевого графика составим линейный график, а затем, используя его, составим график интенсивности использования ресурсов. Для построения графика интенсивности использования ресурсов над каждой работой проставляется потребность в ресурсах. Проецируем на ось времени начало и конец каждой работы. Подсчитываем сумму ресурсов для каждого дня выполнения проекта. Полученные суммы наносим на график интенсивности использования ресурса. Пунктирная линия проводится на уровнеR ограничения наличного ресурса.

. Основные характеристики моделей управления запасами.

1. Спрос на запасаемый продукт может быть детерминированным( в простейшем случае-0 постоянным во времени) или случайным.

2. Пополнение склада может осуществляться либо периодически, либо по мере исчерпания запасов.

3. Объём заказа. Заказ обычно подаётся на одну и ту же величину при достижении запасом заданного уровня – точки заказа.

4. Время доставки. В идеализированных моделях управления запасами предполагается, что заказанное пополнение доставляется на склад мгновенно. В других моделях рассматривается задержка поставок на фиксированный или случайный интервал времени.

5. Стоимость поставки слагается из 2 компонент- разовых затрат, которые не зависят от объёма заказываемой партии, и затрат, зависящих (чаще всего – линейного) от объема партии.

6. Издержки хранения. За хранение каждой единицы запаса в единицу времени взимается определённая плата.

7. Штраф за дефицит. Отсутствие запаса в нужный момент приводит к убыткам, связанных с простоем оборудования, неритмичностью производства ит.д. Эти убытки называются штрафом за дефицит.

8. Номенклатура запаса. На складе хранится запас однотипных изделий или инородного продукта. В более сложных случаях рассматривается многономенклатурный запас.

Возможные графики изменения запасаQ изменяющегося на складе во времени t.

. Системы регулирования запасов.

Рассм. наиболее простые системы регулирования тов. Запасов, кот.основаны на различных стратегиях пополнения запасов:

1. С-ма с фиксированным размером заказа, в кот. Размер заказа на пополнение запаса величина постоянная.

Регулирующие параметры системы:

1. Размер заказа, т.е. величина партии поставки

2. Точка заказа

2. С-ма с фиксированной периодичностью заказа. При этой системе заказы на очередную партию повторяются через равные промежутки времени. В конце каждого периода проверяется уровень запасов и исходя из этого определяется объем заказанной партии. Запас пополняется каждый раз до определённого уровня, не больше мах запаса.

Регулирующие параметры системы:

1. мах уровень запасов

2. продолжительность периода повторения заказа

1. Саморегулирующие системы имеют изменяющийся период и размер заказа и учитывают неопределённые условия

В каждой из рассматриваемых систем определяется целевая ф-ция, кот. Служит критерием оптимальности работы системы.

Критерий эффективности- функция затрат( издержек), которые являются суммарными затратами на хранение и поставку запасаемого продукта и затраты на штрафы. Задача управления запасами состоит в отыскании точной стратегии пополнения и расхода запаса, при котором функция затрат min.

Ф-ия затрат:

L1- затраты, связанные с организацией заказа и его реализацией( организационные издержки)

L2- издержки, связанные с приобретением запасов. Их учитывают, если цена единицы продукции зависит от величины партии. Количество товара, поставляемого на склад- размер партии

L3- затраты, связанные с хранением запаса( издержки содержания запасов)

L4- потери из-за дефицита.

. Основная модель управления запасами (параметры модели и предположения о работе идеального склада). Формула Уилсона

Эта модель позволяет определить такой размер партии, кот. минимизируют расходы на организацию заказа. Оптимальная партия поставки сост. из следующих допущений: уровень запаса уменьшается равномерно с интенсивностью спроса. В момент, когда все запасы исчерпаны подаётся запас на поставку партии размером q единиц. Заказ выполняется мгновенно, и уровень запасов восстанавливается до мах, равного q единиц. Накладные расходы, связанные с размещением заказа и поставкой не зависят от величины партии. Издержки содержания единице товара на складе в единицу времени на складе, а стоимость товара s, срыв поставок не допустим

Формула определяет оптимальный размер партии поставки. Она называется формулой Уилсона

Индексивность спроса  [ед. товара в год]. Предположения: спрос непрерывен и равномерен, весь спрос удовлетворяется

Организ. издержки к [ден. ед-ц в год]. Предположения: издержки постоянны, независят от размера партии.

Стоимость товара S [ден. ед-ц за 1 товара]. Предположения: цена товара не меняется в течении года.

Издержки хранения запасов h [ден. ед-ц за 1 товара в год]. Предположения: издержки постоянны в течении года.

Длина цикла t=q/u [года].

Размер партии q [ед-ц товара]. Предположения: размер партии постоянен, поступление товара происходит мгновенно, как только уровень запаса =0.

Формула Уилсона. Характеристическое свойство оптимального размера партии. Расчетные характеристики работы склада в оптимальном режиме

Для того чтобы определить мин. издержки нужно определить оптимальный размер партии поставки товара Ф-ция L=kט/q +sט+hq/2 – ф-ция одной переменной и чтобы найти мин этой функции найдем её производную и прировняем к 0

dL(q)/dq=0

dL(q)/dq= - kט/q² + 0 +h/2

dL(q)/dq= - kט/q² + h/2 =0

q= - ф-ла Уилсона

Размер партии q оптимален тогда и только тогда, когда организационные издержки равны издержкам хранения запаса

График

При увеличении партии поставки орг. издержки уменьшаются, а издержки хранения увеличиваются и наоборот.

Расчётные характеристики работы склада в оптимальном режиме

Используя формулу Уилсона можно получить

1. оптимальный средний уровень запаса

q_опт=q_опт/2

2. оптимальная периодичность пополнения запаса(время между поставками)

τ_опт=

3. мин. З-ты

L_min=

Иногда будет задана не интенсивность спроса υ, а общее потребление запасаемого продукта Q за время Т – плановый период

Q=υT

4.оптимальное число поставок

n_опт =

5.относительное имение объёма партии по сравнению с оптимальным

∆q/q_опт = (q+q_опт)/q_опт

6. относительные суммарные з-ты

∆L/Lmin=(L+Lmin)/Lmin=1/2(∆q/q_опт)²

. Основная модель управления запасами. Точка заказа

Рассм. работу склада, на котором хранятся товарные запасы, расходуемые на снабжение потребителей. Эта модель позволяет определить такой размер партии, кот. минимизирует расходы на организацию запасов и содержание их на складе. Уровень запаса снижается равномерно с интенсивностью  (спрос). В момент, когда все запасы исчерпаны, подается заказ на поставку новой партии размером q единиц. Заказ выполняется мгновенно и уровень запасов восстанавливается до мах., равного q единиц. Накладные расходы, связанные с размещением заказа и поставкой партии, не зависят от объема партии и равно поставляемой величине . Издержки содержания единицы товара на складе в единицу времени равны h, стоимость товара равна S. Срыв поставок недопустим!!!

Длина цикла =q/

Составим мат. модель работы склада(определим издержки).

Изд-ки за время :

L_ц=+hq²/2

Разделим на  получим издержки в единицу времени:

L(q)=/q + S + hq/2,

Где L₁=/q , - организационные издержки;

L₂= S, -стоимость товара;

L₃= hq/2,- издержки хранения;

Определим оптимальный размер партии поставки товара q_{опт :}

dL(q)/dq = 0

dL(q)/dq = - /q² + 0 + h/2

-/q² + h/2 = 0

q = 2/h – ф-ла Уилсона

Точка заказа.

Для бесперебойного снабжения заказ должен подаваться тогда, когда уровень запаса достаточен для удовлетворения потребностей на время выполнения заказа. Этот уровень называется точкой возобновления заказа (r). Для систем, не допускающих дефицит, заказ должен размещаться тогда, когда величина наличного запаса равна:

r=- [/_опт] q_опт

Для бездефицитной работы системы нужно иметь минимальный наличный запас I₀ = .

I >=  - фактический запас для бездефицитной работы

Время потребления наличного запаса t=I₀ / . Чтобы заказанная партия прибыла к моменту полного исчерпания запаса ее нужно размещать в момент :

t₀= I₀ / - ,

а все остальные партии в следующие моменты времени :

t_k= (I₀ / - ) + _опт , =0,1,2…..

.Модель производственных запасов

Пусть товары на склад поступают непрерывно в течение некоторого времени (напр.поступление происходило прямо с произв. линии).Модель в этом случае назыв. МПЗ. Обозначим через  скорость поступления на склад товара в ед. врем. Остальные обозначения и предположения такие же, как и для основной модели управления запасами ,т.е. на склад товар поступает партиями размером q, при этом каждая новая партия начинает поступать на склад тогда, когда уровень запасов упадет до 0.Данная с-ма может работать без дефицита, если интенсивность поступления товара превосходит интенсивность спроса, т.е. q  . Задача сост. в определении оптимального размера партии, минимиз-го общие з-ты. График изменения запасов данной модели имеет вид……

В течение времени ₁ запас одновременно поступает и расходуется, в теч вр. ₂ происходит только расход запаса. Длина цикла равна:

₁+₂

За время  происх. расход запаса. Mах. величина запаса дан. модели:

_m=q(1)

Общие издержки дан. сист. в ед. времени и для основной системы управления запасами сост.:

L(q)=L1+L2+L3= kq+S+hq()/2

Чтобы определить q_опт, найдем dl/dq и приравним к 0.

kq² + h(-)/2

q_опт=