26 Временные ряды(вр),их классификация. Составляющие вр

Для характеристики и анализа различных соц.-эк. явлений за опред. период применяют показатели и методы, характеризующие эти процессы во времени. Под ВР в экономике понимается последовательность наблюдений некоторого признака (СВ) у в последовательные моменты времени. Отдельные наблюдения наз. уровнями ряда,кот-ые обозначаются y_t (t=1,2,…,n),где n-число уровней. Последовательно расположенные во времени числовые показатели характер-ют уровни состояния или изменения явления или процесса. Классификация ВР:1)в зависим-и от показателя времени ВР бывают моментные,т.е. на опред. дату, и интервальные, т.е. за опред. период 2) по форме представления уровни во ВР м.б. представлены абсолютными, средними и относительными величинами 3)по расстоянию между уровнями ВР подраздел-ся на ряды с равностоящими и неравностоящими уровнями по времени. 4)по содержанию показатели ВР подразд-ют на стоящие из частных показателей и агрегированных показ-ей. Несопоставимость уровней ВР: при построении ВР необходимо соблюдать опред.правила, нарушение кот-ых приводит к несопоставимости уровней ряда. Несопоставимость уровней ВР может возникать в результате неодинаковой полноты охвата объектов в том случае, если показатель представлен в различных единицах измерения, из-за сезонных явлений и т.д.Составляющие ВР: В общем виде при исследовании эк-их ВР y_t выделяются несколько составляющих: y_t=u_t+υ_t+ε_t, где u_t-тренд, т.е. плавноменяющаяся компонента, описывающая длительную тенденцию изменения признака(напр., рост населения, эк. развитие и т.д.), υ_t-сезонная компонента, отражающая повторяемость эк. процессов в течение не очень длительного периода(года, месяца, недели), ε_t-случайная компонента,отражающая влияние не поддающихся учёту и регистрации случайных факторов. Отметим, что первые составл-щие u_t, , υ_t явл. закономерными, неслучайными.

Осн. этапы анализа врем.рядов

1)графическое представление и описание поведения ВР;2)выделение и удаление закономерных(неслуч-ых) составляющих ВР (тренда,сезонных и циклических составляющих);3)сглаживание и фильтрация,т.е. удаление низко- и высокочастотных составляющих ВР;4)исследование случайной составляющей ВР, построение и проверка адекватности матем. модели для её описания;5)прогнозирование развития изучаемого процесса на основе имеющегося ВР;6)исследование взаимосвязи м/различными ВР.

a)Стационарный врем.ряд, коэффициент автокорреляции, автокоррел-ая функция б)Понятие об авторегрессионных моделях

а)Важное значение в анализе ВР имеют стационарные ВР, вероятностные св-ва кот-ых не изменяются во времени. ВР y_t (t=1,2,..,n) наз. стационарными, если совместное распределение вероятностей n наблюдений y₁,y₂,y₃,...,y_n такое же,как и n наблюдений y_1+τ, y_2+τ,y_n+τ, при любых n,t и τ.Коэффициента автокорр-ции. Степень тесноты связи м/последовательностями наблюдений ВР y₁,y₂,y₃,...,y_n и y_1+τ, y_2+τ,y_n+τ (сдвинутых относит-о друг друга на τ-единиц,или как говорят, с лагами τ)может быть определена с пом коэффициента корреляции: ,т.к. М(y_t)=M(y_t+τ)=а,_y(t)=_y(t+τ)=. Т.к. коэфф.r(τ) измеряет корреляцию м/уровнями одного и того же ВР, его наз. коэфф. автокорр-ции. Зависимость r(τ)-также наз. автокорр-ционной ф-ей. В силу стационарности ВР y_t(t=) автокорр-ая ф-я зависит только от лага τ,причем r(-τ)=r(τ).

б)В эконометрике достаточно шир. применение получили регрессионные модели, в кот-ых регрессорами выступают лаговые переменные.Лаговая переменная-перем-ая, влияние кот-ой в эконометрической модели характ-тся некоторым запаздыванием. Авторегрессионная модель р-го порядка (или модель АК(р)) имеет вид: y_t=β₀+β₁∙y_t-1+ β₂∙y_t-2+…+ β_p∙y_t-p+ε_t,где β₀, β₁,…, β_р-некоторые константы. Она описывает изучаемый процесс в момент t в завис-и от его знач-ий в предыдущие моменты t-1,t-2,…,t-p.

Прогнозирование на основе моделей врем.рядов(ВР)

Одна из важнейших задач анализа ВР состоит в прогнозировании на его основе развития изучаемого процесса. При этом исходят из того,что тенденция развития, установленная в прошлом может быть распространена на след. период.Задача ставится след.обр.:имеется ВР y_t(t=) и треб-ся дать прогноз уровня этого ряда на момент n+τ.Если рассм-ть ВР как регрессионную модель изучаемого признака по переменной «время»,то к нему можно применить след. методы анализа ВР:-корреляционный,-модели авторегресси,-модели скользящей средней.Далее будем полагать,что возмущения ε_t(t=) удовлетворяют предпосылкам регрессионного анализа, т.е. условиям Гаусса-Маркова.

Экономический анализ при нарушении классических предположений

При моделировании реальных эконом. процессов возникают ситуации, в кот-ых условие класс. модели регрессии (условие Гаусса-Маркова)оказываются нарушенными, а при их нарушении метод МНК может давать оценки с плохими стат. св-вами. Проблемы при нарушении класс.предположений.1. Если имеется линейная связь экзогенных переменных, напр.,х₂=b₀+b₁x₁, то МНК-оценки не будет существовать, т.к. не сущ. обратная матрица к матрице Х^'Х, кот-ая будет вырожденной(когда нет обратной матрицы).Такая ситуация в эконометрике носит название проблемы мультиколлениарности.2.Если нарушается гипотеза о взаимной независимости случ-ой переменной, то возникает проблема автокорреляции, в рамках кот-ой МНК-оценки не обладают несмещённостью.3.Одной их ключевых предпосылок МНК явл. условие постоянства дисперсии случ-ых отклонений. Выполнимость данной предпосылки наз. гетероскедастичностью (непостоянством дисперсии отклонений).

Обнаружение гетероскедастичности(Гск),методы ее устранения,ее последствия.

Проблема Гсквозникает,когда точность наблюдений,проведенных в разл. Моменты времени,неодинакова.

Разл-т явную и неявную Гск.

Явная-случайная переменная имеет различ.дисперсию в различ. моменты наблюдений правильно специфицированной модели.

Неявная-возникает вследствие неправильной спецификации модели

Последствия Гск:

1)смещение оценки параметров.

2)дисперсия оценок параметров возрастает,что означает меньшую их значимость.

3)недооценка величин дисперсий МНК –оценок параметров,т.к. t и F-критерии не позволяют распознать эту проблему.

Методы диагностики:

1)критерий Парка.

2)критерий Голдфелда-Кандта.

3)критерий Уайта.

Автокорреляция,ее основные причины и последствия.

Важной предпосылкой построения кач.регрес.модели по МНК явл-сянезавис-ть значений случ-х откл-нийот знач-ийоткл-ний во всех др. наблюдениях.

Автокор-ция-(последовательная коррел-ция) опред-тся как корреляция между наблюдаемыми показателями, упорядоченными во времени (ВР) или пространстве (перекрестные данные).

Причины ее появления:

1)ошибки спецификации-неправ.выбор формы зависимости,обычно приводит к систем.отклонениям точек набл-ий от линии регрессии,что может вызвать появл-иеавтокор-ции.

2)инерция-многие эк-ие показатели(напр, инфляция,безраб-ца,ВНП) обладают опр-ой цикличностью,связанной с волнообразностью деловой активности.

3)эффект паутины-во многих пр-ныхи др. сферах эк-ие показ-ли реагируют на изменение эк. условий с запаздыванием.

4)сглаж-ие данных-если данные по некотор.продолжительному временному периоду получают усреднением данных по сост-щим его подынтервалом, то это может приводить к появлению автокор-ции.

Последствия автокор-ции:

1)оценки параметров,оставаясь линейными и несмещенными,перестают быть эф-ыми.

2)дисперсии оценок явл.смещ-ными.Частодисперсии,вычисляемые по стандарт.формулам,явл.заниженными,что влечет за собой увел-е t-статистик.

3)оценка жисперсии регрессии явл-сясмещ-ой оценкой истинного значения,вомногих случаях занижая его.

4)выводы по t- и F-статистикам, определяющим значимость, определяющим значимость к-тов регрессии и к-та детерминации,возможно будут неверными.Вследствие этого ухудш-тся прогнозные кач-ва модели.

Обнаружение и устранение автокор-ции.

1)графич-ий метод-по оси абсцисс откладывают время получения стат.данных,либопорядк.№ набл-ния,а по оси ординат отклонения.Отсутст-вие завис-ти скорее всего свид-ет об отсутствии автокор-ции.

2)Тест Дарбина-Уотсона-критерий оценки основан на решающей функции

На основании статистики d можно сделать след.выводы:

а)если d=0,то r=1 (r-выборочный коэф-т автокор-ции-полож-аяавтокор-ция)

б)если d=4,то оценка к-та автокор-цииr= -1-отрицат-ая автокор-ция.

в)промежут.знач-ие ф-цииd=2 позв-ет судить об отсутствии автокор-ции.

Устранение автокор-ции:

Т.к.автокор-ция вызывается неправ-й спецификацией модели,тонеобх-мо прежде всего, скорректировать саму модель.

Возможно,автокорр-ция вызвана отсутст-вием в модели некоторой важной объясняющей переменной.

Следует попытаться опр-ть данный фактор и учесть его в ур-нии регрессии.

Также можно попроб-ать изменить ф-лу зависимости.

Мультиколлинеарность,ее последствия и причины устранения.

Если в модель включаются 2 и более тесно взаимосвяз-ых ф-ров, то наряду с уравнением регрессии появл-тся и др.зависимость.

Мультикол-сть-тесная зависимость между факторными признаками,включенными в модель.Она искажает величину коэф-тов регрессии и затрудняет их экономич. Интерпритацию.

Причины возникновения:

1)изучаемые факторные признаки характеризуют одну и ту же сторону явления или процесса(показатели обьема произведенной продукции)

2)использ-ние в кач-ве факторных признаков величин,суммарное значение кот. Предст.собойпостоянн.величину.

3)факторные признаки,являющиеся элементами др.друга (затраты на пр-во, с/, ед-цы продукции)

4)факторные признаки,поэкономич-ому смыслу дублирующие др.друга(прибыль,рентабельность)

Последствия:

Большие дисперсии оценок.

Уменьшается t-статистики коэф-тов, что может принести к неоправданному выводу о существенности влияния соответствующей объясняющей переменной на зависимую переменную.

Оценки коэф-тов по МНК и их стандартные ошибки становятся очень чувствительными к малейшим изменениям данных.

Затрудняется определение вклада каждой из объясняющей переменной (объясняемую уравнением регрессии) дисперсию зависимой переменной.

Определение мультиколл-сти и методы ее устранения.

Способы определения:

1)анализ матрицы коэф-тов парной корреляции.Ф-рыи могут быть признаны коллинеарными если›0.8

2) исслед-ниематрицыx'x. Если определитель этой атрицы близок к 0,то это свидетельствует о наличии мультиколл-сти.

3)коэф-т детерминации достаточно высок,но некоторые из коэф-тов регрессии статистически незначимы,т.е. имеют низкие t-статистики.

4)высокие частные коэф-ты корреляции.

Методы устранения:

1)сравнения значений линейных коэф-тов корреляции

2)метод включения ф-ров.(метод пошаговой регрессии)

В модель включаются ф-ры по одному, в определеннойпоследоват-сти.

3)метод исключения ф-ров. В модель включаются все ф-ры.Затем после постороенияуравн-ния регрессии из модели исключают ф-р,коэф-т при кот. Незначим и имеет наименьшее знач-ниеt-критерия.Получают новое уравнение регрессии и снова проводят оценку значимости всех оставшихся коэф-товрегресссии.

4)получение дополнит-ых данных или новой выборки. При др. выборке мультикол-сти не будет либо она не будет столь серьезной.Иногда для уменьшения мультикол-сти достаточно увеличить объем выборки.

5)изменение спецификации модели.Либоизменятеся форма модели, либо добавляютя объясняющие переменные,неучтенные в первонач-ной модели,но существ-но влияющие на зависимую переменную.

Задачи ЭММ

1). анализ эконом-х объектов и процессов

2). эконимич-ое прогнозиров-ие развития эконом-х процессов

3). выработка управленческих решений на всех уровнях хоз-ой иерархии

Этапы ЭММ

1).анализ законов, описыв-их связи основных объектов(переменных) модели

2 ). теорет-ое исслед-ие построенной мат.модели – реш-ие прямой задачи и, как следствие, исследов-ие св-в эндогенных переменных и их сопоставление с реальными наблюдениями изучаемых явлений.

3). проверка адекват-ти модели, т.е. выяснение того, согласуется ли гипотетич-ая(построенная) мат.модель с моделируемым экон-им процессом.

4). последующий анализ с уточнением мат.модели с учетом накопл-х данных об изучаемом экон-ом процессе.

Экономико-математическая оптимизационная модель.

1.Мат-ое описание иссл-го экон-го объекта или соответствующих экономических процессов, т.е. входных и выходных переменных, перем-х текущего состояния объекта и перем-х которыми можно управлять-управлений, а также существующих м-ду перем-ми зависимостей.

2.Ограничения на управления-класс допустимых управлений.

3.Ограничения на переменные, вытекающие из экономического смысла задачи.

4.Цель управления-критерий каческтва – выбранный количественный показатель эффективностиуправления, обычно представляющий собой фун-ию (целевую) экзогенных (велечин) переменных.

Модели оптимального планирования в промышл-м и аграрном комплексе

Современное промыш-ое предпр-ие хар-ся высоким уровнем развития производств. сил и увелич-ем темпов НТП. В рыноч-х услов-х хозяйств-ия выбор оптимального вар-та управл-ия и планир-ия произв-ва усугубляется конкуренц-ей товаропроизв-ва внутри страны, а так же потоками товаров, услуг и капитала из др.стран.

Обосн. решение нельзя принимать без изучения и анализа большого объема эконом-ой инфо-ии, характер. на каждом конкретном предприятии эффектив-го использ-ия трудовых, материальных и денежных рес-ов, а также конъюнктуру рынка.

Критерии и оценки хоз.деят-ти предпр-ия

1). чистый доход понимается как разность между стоим-ю продаваемой продукции и затратами на ее произ-во.

2). показ. прибыли

3). рентабельность определ-ся как отнош-ие прибыли к среднегод-ой стоим-ти производств-х фондов.

4). показ. реализ-ии прод-ии.

5). произв. труда опред-ся как выработка товарн. продукции на одного работника

6). максимум загрузки оборудования

Сис-ма огранич. ЭММ задачи определения производств-го плана предпр-ия должна учитывать производст-ые рес-сы и специфич-ие условия работы предпр-ия в его продукции.

Виды оптимизац. моделей.

В завис-ти от вида целевой фун-ии и ограничений оптимизац-ые модели бывают:

1). Если огранич. и целевая фун-ия линейны относительно переменных, то модель называется линейной.

2). Если хотя бы одна из фун-ий нелинейна, то модель называетяс нелинейная.

3). Если пар-ры управл. могут принимать лишь целые значения, при решении подобных задач используется целочисленное программирование.

4). Если исходные параметры задач могут изменятся в заданных пределах, для их решения применяют параметрическое программирование.

5). Если параметрическая целевая фун-ия или сис-ма ограничений изменяется во времени, или сам процесс выработки решения имеет многошаговый хар-р, то такие задачи решаются метдом динамического программирования.

После построения модели осущ-ся поиск оптимального решения. В завис-ти от вида оптимизац-ой модели используют различные методы мат.программирования.

Задача оптимизации производств-ой прогр-мы предприятия

Предпр-ие выпускает n-видов продукции n_j, j=1,n, имея ограниченный запас рес-ов p_i, i=1,m.

Известны:

a_ij - нормы затрат рес-ов p_i на произ-во единицы продукции p_j

c_j – эффективность единицы продукции (например, цена).

Требуется найти такой план производства продукции, который обеспечивает максимум эффекта от выручки (максимум выручки от реализации или мин.затрат).

Математическая модель и экономическая интерпретация задачи рационального использования ресурсов и двойственной к ней

Математическая модель задачи:

Пусть xj-объем производства продукции j-ого вида j=. Максимизируется выручка от реализации продукции: Z=c1x1+c2x2+…+cnxn →max– целевая функция. Ограничения на запас i-ого ресурса: , где - расход i-ого ресурса на производство всех n видов продукции в количествах x1,x2,…,xn соотв-нно, - запас ресурса.Условие неотрицательности переменных: , j=.

Двойственная задача. Пусть уi – оценка ресурса. Тогда суммарная оценка ресурсов будет минимизироваться: F(y)=b1y1+b2y2+…+bmym→min

Условие неотрицательности переменных: , j=. Согласно теоремам двойственности, если одна из двойственных задач имеет оптим. решение, то и вторая также имеет оптим. решение.

Понятие о методе межотраслевого баланса. Балансовая модель. Межотраслевой баланс в общем виде

Балансовая модель- с-ма уравнений, каждое из которых выражает требование баланса между производимым отдельными экономическими объектами, количеством продукции и совокупной потребностью в этой продукции. Балансовые модели как статистические, так и динамические, широко применяются при экономико-математическом моделировании экономических с-м и процессов.

Балансовый метод- метод взаимного сопоставления имеющихся материальных, трудовых и финансовых ресурсов и потребностей в них. Примерами балансовых соответствий могут быть: соответствие наличия рабочей силы и количества рабочих мест; платежеспособного спроса населения и предложения товаров и услуг и т.д.

Балансовые модели не содержат какого-либо механизма сравнения отдельных вариантов экономических решений, что не позволяет сделать выбор оптим. варианта развития экон. с-мы. Балансовые модели строятся в виде числовых матриц, поэтому они относятся к матричным экономико-математическим моделям.

Рассм. след. виды балансовых моделей: 1).частные материальные, трудовые и финансовые балансы для народного хозяйства и отдельных отраслей; 2).межотраслевые балансы; 3).матричные финансовые планы предприятий и фирм.

Межотраслевой баланс(МОБ) является моделью экономики - таблицей, в кот. показываются многообразные натуральные и стоимостные связи в экономике. Совокупный общественный продукт – масса произведенных или планируемых к производству материально-вещественных благ и услуг. В стоимостном выражении совокупный общественный продукт делится на: перенесенную стоимость(износ средств труда и расход предметов труда), вновь созданную стоимость (нац. доход). В натуральном МОБ отражается движение совокупного общественного продукта по его материально-вещественному составу, что позволяет определить затраты конкретных видов ресурсов на производство продукции и на этой основе найти общ. Потребности в ассортименте и объемах продукции, определяет целесообразные темпы и пропорции развития отдельных отраслей. Чистые(технологич.)отрасли – некоторые условные отрасли, кот. объединяет све производство данного вида продукта независимо от ведомственной подчиненности субъектов хозяйствования, их производящих. МОБ строятся на основе след. предположений: 1).каждая отрасль производит только 1 продукт; 2).Каждая отрасль как бы имеет только 1 технологию производства продукции, кот. хар-ся средневзвешенными коэффициентами затрат.

Состав и характеристика 4-х квадрантов межотраслевого баланса

Разделы МОБ. В общем виде МОБ состоит из 4 разделов, кот. называются квадрантами.

I	II
III	IV

Основным является I квадрант, т.к. его данные используются во всех расчетах и являются их основой. Во II квадранте хар-ся непроизводственная сфера. В I и III квадрантах хар-ся текущие затраты материального производства, во II и IV – оказывается использование продукции за пределами текущего производственного цикла. Различают натуральный и стоимостной баланс.

Стоимостной межотраслевой баланс. Цены, используемые при разработке стоимостного баланса

Стоимостной МОБ или МОБ производства и распределения в денежном выражении состоит из 4-х квадрантов, по каждому из кот. показатели баланса рассчитываются в стоимостном выражении. Основное назначение стоимостного МОБ состоит в том, чтобы сопоставить затраты с доходами(по стране в целом или по тому или иному региону.)

Виды стоимостного МОБ: 1).Отчетный баланс. На основе отчетного стоимостного баланса проверяется в какой мере затраты компенсированы доходами. 2).Плановый баланс. Позволяет сопоставить планируемые затраты с возможными доходами.

Валовая продукция – объем произведенной продукции в денежном выражении. Промежуточный продукт отрасли – в стоимостном выражении произведенные затраты этой отрасли в других отраслях экономики в качестве предметов труда, т.е. это стоимость текущих материальных затрат. Конечный продукт отрасли – стоимость продукции отрасли, направляемой на накопление и потребление. Чистая продукция отрасли – стоимость созданной в процессе производства или планируемой к производству продукции данной отрасли. Чистая продукция отрасли состоит из оплаты труда и чистого дохода отрасли.

Единая система цен. При разработке стоимостного баланса могут быть использованы следующие цены: 1).фактические цены производителя. Они показывают, сколько стоит продукт в месте его производства(не учитываются транспортно-заготовительные расходы). В ценах производителей рекомендуется строить плановые стоимостные баланса. 2). фактические цены конечного потребления. Они включают затраты, связанные с реализацией продукции и отражают стоимость продукта в месте его потребления. Отчетные стоимостные балансы строятся в ценах конечного потребления. 3).Расчетные цены. Они соответствуют действительным издержкам производства продукции каждой отрасли.

Состав и характеристика 4-х квадрантов стоимостного МОБ

Стоимостной МОБ состоит из 4-х квадрантов, каждый из которых хар-ет отдельные стороны или процессы расширенного производства. Важнейшей частью стоимостного МОБ является I квадрант, поскольку он хар-ет межотраслевые связи в сфере материального производства. I квадрант – таблица размерности nxn, наименование строк и столбцов которой соответствует чистым технологическим отраслям материального производства. В строках и столбцах в одинаковом порядке перечислены одни и те же отрасли материального производства (табл.1).

Обозначения: Xi – валовой выпуск продукции i-ой отрасли за рассматриваемый промежуток времени, xij – межотраслевые потоки продукции от i-ой отрасли к j-ой отрасли, xii- главная диагональ МОБ, ее элементы стоят на пересечении строк и столбцов одноименных отраслей и хар-ют внутреннее потребление каждой отраслью своей же продукции, Yi – объем продукции отрасли i, потребляемый в непроизводственной сфере, - конечное потребление. Рассм. МОБ для 3-х отраслей народного хоз-ва.

Табл.1.

Производящие отрасли	Потребляющие отрасли				Конечное использование	Валовой продукт
	1	2	3
1	x11	x12	x13	Y1		X1
2	x21	x22	x23	Y2		X2
3	x31	x32	x33	Y3		X3
Условно-чистая продукция	Z1	Z2	Z3
Валовой продукт	X1	X2	X3

Строки I квадранта отражают межотраслевые поставки сырья, материалов, топлива и т.д. отраслям материального производства в денежном выражении.

Столбцы I квадранта стоимостного баланса хар-ют состав материальных затрат в денежном выражении на производство продукции отдельных отраслей.

Во II квадранте МОБ хар-ет конечное потребление каждого вида продукции.

Чистая продукция – сумма оплаты труда Vj, j=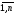 и чистого дохода отраслей mj, j=. Сумму амортизации Cj, j= и чистой продукции некоторой j-ой отрасли называется условно чистой продукцией и обозначаются Zj=cj+Vj+mj, j=.

В III квадранте МОБ хар-ся затраты живого труда и ОПФ, учавствующих в производстве каждого вида продукции отраслей.

IV квадрант баланса находится на пересечении столбцов II квадранта (конечной продукции) и строк III квадранта (условно чистой продукции). Этим определяется содержание квадранта: он отражает конечное распределение и использование национального дохода.

Основные соотношения МОБ

Рассматривая схему баланса по столбцам, получаем, что итог материальных затрат любой потребляющей отрасли и ее условно чистой продукции = валовому продукту этой отрасли:

Xj =+ Zj , j=1,n (1)

Рассматривая схему МОБ по строкам для каждой производящей отрасли получим, что валовый продукт отрасли = сумме материальных затрат отраслей, потребляющих эту продукцию, и конечной продукции этой отрасли:

Xi =+Yi , i =1,n (2)

Просуммируем по всем отраслям уравнение (1):

=

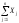Аналогичное суммирование уравнений (2) даёт:

=



Данное равенство показывает, что в МОБ соблюдается важнейший принцип единства материального и стоимостного состава национального дохода.

Модель Леонтьева. Расчеты, кот. можно выполнить с помощью этой модели

Различают математические модели отчётного и прогнозного МОБ. Модель отчётного МОБ выражается в виде 2 групп соотношений, которые описываются формулами Xj =+ Zj , j=1,n и Xi =+Yi , i =1,n. Однако для прогнозных расчётов соотношения ур-ний (1) и (2) мало пригодны в силу сложности подсчёта элементов промежуточного потребления _xij Коэф-т прямых затрат (коэф-т материалоёмкости) вычисляется по формуле: aij = xij/Xj, j=1,n (3) и показывает какое количество продукции i-той отрасли необходимо, учитывая только прямые з-ты для пр-ва единицы валовой продукции j-той отрасли.

Коэф-т прямых затрат является довольно стабильной величиной во времени.

Из формулы (3) следует, что межотраслевые потоки прод-ции можно определить по формуле: x_ij = a_ij*X_j (4).

Систему уравнений баланса (с учётом формулы (4)) можно записать в виде:

Xi = a_ij*X_j + Y_i , i=1,n (5)

МОБ в матричной форме: X = A*X + Y (6), где Х-вектор-столбец валовой продукции, У-вектор-столбец конечной продукции. А=( a_ij )_nxn – матрица коэф-тов прямых материальных затрат.

С учётом эк-кого смысла задачи, все коэф-ты матрицы А и компоненты векторов Х и У должны быть неотрицательны.

Системы ур-ний (5) или (6) называется экономико-математическими моделями прогнозного МОБ (моделью Леонтьева, моделью “затраты-выпуск”).

Расчёты, выполняемые по модели:

1.Задавая в модели величины валовой продукции каждой отрасли (Х_i), можно определить объем конечной продукции в каждой отрасли Yi:

Y = (E – A)*X (7)

2.Задавая величины конечной продукции всех отраслей (Yi) можно определить величины валовой продукции каждой отрасли (Xi):

X = (E –A)^-1*Y (8)

3.Для ряда отраслей - задавая величины валовой продукции, а для всех остальных отраслей - объемы конечной продукции можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых, в этом случае удобнее пользоваться системой уравнений (5).

В формулах 7 и 8 Е- единичная матрица, (E –A)^-1 – обратная матрица.

Условно чистая продукция определяется по формуле: Z_j=X_j=

- балансовое соотношение данной модели.

Матрица коэф-тов полных затрат.

Обозначим обратную матрицу (E – A)^-1 через В, тогда модель (8) можно записать в виде X = B*Y

Матрица В=(b_ij)_nxn есть матрица коэф-тов полных затрат.

Коэф-ты полных затрат можно применять тогда, когда необходимо определить, как скажется на валовом выпуске некоторой отрасли предполагаемое изменение объёмов конечной прод-ции всех отраслей.

дельтаXi = b_ij*дельтаY_i; i=1,n, где дельтаXi, дельтаY_i - изменения (приросты) величин валовой и конечной продукции соответственно.

. Динамические модели МОБ

Рас-е ранее модели межотраслевого баланса явл-ся статическими, т.е. такими, в которых все зав-ти отнесены к одному моменту времени. Эти модели могут разрабатываться лишь для отдельно взятых периодов, причем в рамках данных моделей не устанавливается связь с предшествующими или последующими периодами. В стат. моделях не анализируется распределение использования и про-я эф-ть капитальных вложений. Капиталовложения вынесены из сферы про-ва в сферу конечного исп-я вместе с предметами потребления и непроизводственными затратами, т.е. включены в конечный продукт. В отличии от статических, динамические модели должны отражать не состояние, а процесс развития экономики, устанавливать непосредственную связь м/ду предыдущими и последующими этапами. В основе построения моделей в виде динамической системы лежит математическая зав-ть м/ду величиной капитальных вложений и приростом продукции.

Уравнения распределения продукции вида в динамической модели преобразуется в след.где (х_ij)_nxn – матрица межотраслевых потоков текущих затрат. Элементы этой матрицы совпадают с соответствующими элементами статич. баланса. ()_nxn – матрица межотраслевых потоков капитальных вложений.Элементы этой матрицы показывают показывают какое количество продукции i-той отрасли направлено в текущем периоде в j-тую отрасль в качестве производственных капитальных вложений в ее основные фонды.

уi` - продукция i-той отрасли, идущая в личное и общественное потребление, непроизводственные накопления, прирост оборотных фондов на экспорт и т.д. Таким образом сумма потоков капитальных вложений и конечного продукта динамической модели = конечной продукции статического баланса уi=

. Матричная игра с нулевой суммой

Чтобы задать матричную игру с нулевой суммой необходимо перечислить все возможные стратегии каждой из сторон и определить результат игры для каждой пары таких стратегий. Обозначим возможные стратегии игрока А: A₁, A₂, A₃…A_m.

Стратегии второго игрока В: В₁, В₂, В₃…В_n.

Если игрок А применит стратегию А_i, то время как игрок В применяет стратегию В_j, то рез-том такого решения будет выйгрыш игрока А равный а_ij, а для игрока В вел-на а_ij будет пройгрышем. Матричная игра с нулевой суммой полностью задаётся платёжной матрицей игры.

= [a_ij]_mxn

Если в игре исп-ютя случайные ходы, то исход игры определяется средним значением выйгрыша (мат. ожиданием). В платёжной матрице записываются всегда выйгрыши игрока А. Число α = max_i α_i = max_i min_j a_ij называется нижней чистой ценой игры (максмином). Оно показывает, какой минимальный выйгрышможет получить игрок А, правильно применяя свои чистые стратегии при любых действиях игрока В. Соответствующая стратегия называется максминной. Число β = min_j β_j = min_j max_i a_ij называется верхней чистой ценой игры (минимаксом). Оно показывает максимальный проигрыш игрока В.

. Чистые и смешанные стратегии. Реш-е матр.игры в чистых стр-гиях

Чистые стратегии.

Чистая стр-гия А_i – чистая стр-гия игрока А (В_j – игрока В) – это возможный ход первого (второго) игрока, выбранный им с вер-тью 1.

Если 1-ый игрок имеет m чистых стр-гий, а 2-ой – n чистых стр-гий, то для любой пары стр-гий 1-ого и 2-ого игрока чистые стр-гии можно представить в виде единичных векторов. Для пары стр-гий А₁ и В₂ – чистые стр-гии записываются в виде:

Для A: p=(1;0;…;0) m штук

Для B: q=(0;1;…;0) n штук

Теорема 1

В матр.игре нижняя чистая цена игры не превосходит верхней чистой цены игры, т.е. α≤β.

Решение матричной игры чистой стратегии: Если для чистых стратегий А_i и В_j игроков А и В соотв-но имеет место равенство α=β, то пару чистых стратегий (А_i, В_j) наз. седловой точкой матричной игры. Эл-т a_ij платёжной матрицы называется седловым эл-том.

Число υ=α=β наз-ся чистой ценой игры. Т.о. если матричная игра имеет решение чистой стратегии, то платёжная матрица имеет седловую точку и чистые стратегии обращающие эту седловую точку будут оптимальными. В этом случае оптимальным решением игры считается тройка объектов (А_i, В_j, υ). Платёжная матрица может иметь несколько седловых точек.

Смешанные стратегии.

Если α< β, то игрок А стремится увеличить выйгрыш, а игрок В – уменьшить пройгрыш. Поиск такого решения приводит к использованию сложной стратегии, сост. в случайном применении чистых стратегийс определёнными частотами. Такая стратегия называется смешанной.

Смеш-ой стр-гией 1-ого игрока А (2-ого игрока В) наз-ся вектор p=(p₁;p₂;…;p_m), где p_i≥0 i=1,m и ∑p_i=1 (q=(q₁;q₂;…;q_n) q_j≥0 j=1,n ∑q_j=1), где p_i и q_j вер-ти, с которыми игроки А и В применяют свои чистые стр-гии А_i и В_j в ходе игры.

Т.к. игроки выбирают чистые стратегии случайно и независимо друг от друга, игра имеет случайный хар-р и случайной становится вел-на выйгрыша (пройгрыша). Ф-ция f(p;q) = ∑∑a_ijp_iq_j наз-ся платежной ф-цией игры с матрицей [a_ij]_mxn.

. Смешанные стратегии. Теоремы о смешанных стратегиях матричной игры

Если α<β, то игрок А увеличивает выигрыш, а игр. В уменьшает проигрыш. Поиск такого решения приводит к использованию сложной стратегии, состоящей в случайном применении чистых стратегий с определенными частотами. Такая стратегия наз. смешанной. Смешанной стратегией первого игрока А(второго В) наз. вектор p=(p1,p2,…,pm), где pi≥0, i=1,m, ∑pi=1. Для игр. В q=(q1,q2,..,qm),где qj≥0, j=1,n ∑qj=1

Pi и qj- вероятности с которыми игр. А и В выбирают свои чистые стратегии ai и bj в ходе игры.

Т. К. игроки выбирают чистые стратегии случайно и независимо др. от друга игра имеет случ. хар-р и случайной становится величина выигрыша (проигрыша). Функция f(p,q)= наз. платежной ф-цией игры с матрицей [aij]m×n

Оптимальные стратегии. Стратегии p*=(p1,p2,…,pm) и q*=(q1,q2,..,qm) наз. оптимальными, если для произвольных стратегий p и q выполняется условие: f(p,q*)≤f(p*,q*)≤f(p*,q),где (p*,q*)-явл. cедловой точкой функции f(p,q). Исп-е в игре оптимальных смешанных стратегий обеспечивает первому игроку выигрыш не меньший, чем при использовании им любой другой стратегии p.второму игроку- проигрыш не больший чем при исп-ии любой др. стратегии q.

Оптимальное решение. Значение платежной ф-ции при оптимальных стратегиях опред-т цену игры v, т.е. f(p*,q*)=v. Сов-ть оптимальных стратегий и цены игры составляют решение игры. Теорма 1.В смешанных стратегиях любая конечная матричная игра имеет седловую точку. Теорема2. Для того чтобы смешанные стратегии p* и q* были оптимальными для игроков А и В в игре с матрицей [aij]m×n с ценой v, необходимо и достаточно выполнение неравенства: ,i=1,m

,j=1,n

Активные стратегии. Теоремы об активных стратегия

Чистые стратегии игрока, входящего в его оптимальную смешанную стратегию с вероятностями отличными от 0, наз. активными стратегиями игрока.

Теорема. Если один из игроков придерживается своей оптимальной смешанной стратегии, то его выигрыш остается неизменным и равным цене игры независимо от того какую стратегию применяет др. игрок, если только не выходит за пределы своих активных стратегий.

Можно доказать, что число активных стратегий игроков не превышает наименьшего из чисел m и n.

Доминирующие и доминируемые стратегии. Теорема о преобразовании платежной матрицы матричной игры

Пусть игра задана платежной матрицей [aij]m×n. Если asо≥atj, j=1,n, то выигрыш игрока А при стр-гии s будет больше, чем при стратегии t,какую бы чистую стратегию не применил игр. В.

Стратегию As наз. доминирующей, а At-доминируемой.

Т. К. игрок В заинтересован в минимизации проигрыша, доминирующим будет столбец с наименьшейи элеметами.

Если все элементы air≥ail, i=1,m, то игроку В свой выбор выгодно сделать по l- му столбцу. В этом случае стратегия Вl игрока В доминирует над стратегией Вr.

Дублирование стратегии. Если в матричной игре имеем строки(столбцы) с одними и теми же элементами, то такие строки(столбцы), а соответственно и стратегии игроков А и В наз. дублирующими.

В матричной игре доминируемые и дублирующие строки(столбцы) можно опускать, что не влияет на решение игры, но позволяет уменьшить размерность платежной матрицы.

Теорема. Оптимальные смешанные стратегии p* и q* соответственно игроков А и В в матричной игре [aij]m×n с ценой v будут оптимальными и в матричной игре [baij+c]m×n с ценой v’=bv+c, b>0/

Решение матричных игр 2*2

Игра 2×2 явл. Наиболее простым случаем конечных матричных игр. В этой игре каждый из игроков обладает только двумя стратегиями. Если игра 2×2 имеет седловую точку, то ее решение очевидно. Рассмотрим игру

В1 В2

А1 а11 а12

А2 а21 а22

Предположим, что игра не имеет седловой точки, т. Е. α<β. Требуется найти оптимальную смешанную стратегию игроков p*=(p1, p2) и q*=(q1, q2), а также цену игры v.

Очевидно, что в игре 2×2, не имеющей седловую точку, обе стратегии игроков явл. Активными. Поэтому, если игрок А, будет применять свою оптим. смешанную стратегию, то неизменно от действий игрока В, выигрыш его будет = цене игры v.

Игрок А будет применять стратегию А1 с вероятностью p1 и стратегию А2 с вер-тью p2. Если игрок В отвечает своей стратегией В1, то выигрыш игрока А определяется из уравнения: [а11*р1+а21*р2=v]

Если же игрок В будет применять стратегию В2, то выигрыш игр. А не изменится и определ. Равенством: а12*р1+а22*р2=v

Учитывая условие р1+р2=1 получим систему 3х уравнений с 3мя неизвестными

a11р1+а21р2=v

a12p1+a22p2=v

P1+p2=1

Решив эту систему найдем оптимальное решение для игрока А: р*=(р1, з2) и цену игры v.

Аналогично определяется оптимальная стратегия игрока В из системы уравнений:

a11q1+a21q2=v

a21q1+a22q2=v

q1+q2=1

Решив эту систему найдем оптимальное решение для игрока В: q*=(q1,q2)

Сведение МИ к ЗЛП

Рассм. матричную игру с платежной матрицей:

Обозначим через р*=(р1,р2,р3) и q*=(q1,q2,q3) оптимальные стратегии игроков А и В.

Стратегия р* игрока А гарантирует ему выигрыш не меньше цены игры, независимо от выбора стратегии Вj игроком В.

Система уравнений (1)

Где р1+р2+р3=1, pi≥0, i=1,3

Аналогично для игрока В. Стратегия q* игрока В гарантирует ему проигрыш не больше цены игры v, независимо от выбора стратегии Аi игроком А.

(2)

Q1+q2=1, qj≥0, j=1,2

Т.к. элементы платежной матрицы всегда можно сделать положительными, то и цена игры будет больше 0.

Преобразуем системы 1 и 2 , разделив обе части каждого неравенства на положительное число v, и введем новое обозначение: xi=pi/v≥0, yj=qj/v≥0, i=1,3, j=1,2

Получим (3)

X1+x2+x3=1/v, xi≥0, i=1,3

(4)

Y1+y1=1/v, yj≥0, j=1,2

Т.к. игрок А стремится максимизировать цену игры, то обратная величина 1/v будетминимизироваться, поэтому оптимальная стратегия игрока А определяется из ЗЛП следующего вида:

Z(x)=x1+x2+x3→min

При ограничениях (3)

Для игрока В: f(y)=y1+y2→max при ограничениях (4)

Решив пару двойственных задач графическими или симплекс-методом далее опред. решение матричной игры.

V=1/, pi=xi*/=xi*v, qj= yi*/=yj*v

Алгоритм решения матричной игры:

1.Упрощаем платежную матрицу

2.Проверяем имеет ли игра решение в чистых стратегиях

3. если решение находится в смешанных стратегиях, то решаем либо сведением к системе линейных алгебраических уравнений (2×2), либо сведением к ЗЛП.

.Статистические игры. Основные понятия.

Под стат. игрой или игрой с природой мы будем понимать парную матричную игру, в кот. 1 игрок заинтересован в наиболее выгодном для себя исходе игры, а второй игрок-природа (П), совершенно безразличен к результату игры. Предположим, что в игре с природой сознательный игрок А м. Использовать m чистых стратегий: m: A₁,A₂,…..A_m, а 2 игрок П м. реализовать n различных состояний n: П₁,П₂…П_n. Игроку А м.б. известны вероятности q₁,q₂….q_n, с кот. природа реализует свои состояния, но он может и не знать их. Действуя против природы, игрок А м. реализовать как свои чистые стратегии A_i, так и смешанные. Если игрок А в состоянии оценить некоторой величиной а_ij последствия применения каждой своей чистой стратегии A_i при любом состоянии природы П_j, то игру м. задать матрицей.

А=

Игры с природой явл-ся частным случаем матр. игр.

При упрощении платежной матрицы отбрасывать те или иные состояния природы нельзя, т.к. она м. реализовать любое состояние независимо от того выгодно оно или нет. Решение достаточно найти только для игрока А поскольку природа наши рекомендации воспринять не может. Смешанные стратегии приобретают смысл только при многократном повторении игры.

Решение статистич. игры: 1) упростить платежную матрицу. Отбрасывать стратегии природы нельзя (столбики на месте) 2) оценить выигрыш при различных игровых ситуациях(критерий Байеса, Вальда, Гурвица, Сэвиджа. 3) построить и исследовать матрицу риска 4)сделать вывод о выборе наилучшей стратегии.

критерием Байеса:

1. Критерий, основанный на известных вероятностях условий. Пусть известны вероятности q_j состояний природы П, j=1;n.Тогда пользуемся критерием Байеса, в соответствии с кот. Оптимальная считается чистая стратегия A, при которой максимизируется средний выигрыш

=i=1;n

игрока А, т.е. определяется величина:

=

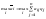
Лапласа:

2. Если объективные оценки состояния природы получить невозможно, но вероятности природы могут быть оценены субъективно на основе принципа недостаточного основания Лапласа, согласно которому все состояния природы полагаются равновероятностными, т.е.

q₁=q₂=…….=q_n= и оптимальной считают стратегию А_i, обеспечивающую максимальное среднее значение выигрыша

=

Если вероятности q_j состояний природы неизвестны и нельзя сделать о них никаких предположений, то пользуемся критериями Вальда, Гурвица, Сэвиджа.