4.3.2. Методы тестирования на автокорреляцию

Существует несколько подходов к тестированию регрессионных остатков на автокорреляцию. Во многих статистических пакетах решение задач по построению регрессии дополняется графическим представлением результатов моделирования. В том числе предоставляется возможность визуализации поведения отклонений во времени. Как правило, строятся либо последовательно-временные графики, либо графики зависимости от .

В первом случае по оси абсцисс откладывается либо время, в которое было получено статистическое наблюдение, либо номер наблюдения, а по оси ординат – отклонение , величина которого становится известной после построения уравнения регрессии.

Рис. 4.1. Зависимость остатков от времени

Анализ графиков, представленных на рис. 4.1, показывает, что в случае а) и б) изменение остатков подчиняется некоторой закономерности и можно предположить, что они автокоррелированы. Случай в) свидетельствует об отсутствии какой-либо зависимости, и предположение о возможной автокоррелированности несостоятельно.

Во втором случае по оси абсцисс откладывается , а по оси ординат – . Тогда, если график будет иметь вид, представленный на рис. 4.2, то есть все основания считать, что остатки автокоррелированы. Причем, так как большинство точек на этом графике расположены в первой и третьей четвертях декартовой системы координат, то можно с уверенностью говорить о положительной зависимости в среднем между соседними отклонениями.

К сожалению, графики остатков не всегда выглядят так убедительно, как на приведенных рисунках. Поэтому, кроме графических, применяются и аналитические методы тестирования на автокорреляцию остатков.

Рис. 4.2. Авторегрессионная зависимость остатков

Метод рядов. Этот метод состоит в следующем. После построения уравнения регрессии последовательно определяются знаки отклонений , например,

(+ + + +) (- - - - - - - -) (+ + + + +) ( - - -) (+ + + +) (-),

т.е. 4 «+», 8 «-», 5 «+», 3 «-», 4 «+», 1 «-» получено при построении модели по выборке из 25 наблюдений.

Будем называть рядом непрерывную последовательность одинаковых знаков. Количество знаков в ряду принято называть длиной ряда.

Интуитивно понятно, что если есть ряды, то, скорее всего, между остатками есть зависимость. Причем, если рядов слишком мало по сравнению с количеством наблюдений, то вполне вероятна положительная автокорреляция, если же рядов слишком много, то вероятна отрицательная автокорреляция. Для более обоснованного вывода предлагается следующая процедура.

Введем обозначения:

– объем выборки;

– общее количество знаков «+» при наблюдениях (количество положительных отклонений );

– общее количество знаков « – » при наблюдениях (количество отрицательных отклонений );

– количество рядов.

При достаточно большом количестве наблюдений (>10, >10) и отсутствии автокорреляции доказано, что случайная величина имеет асимптотически нормальное распределение с

; . (4.111)

Тогда, если окажется, что удовлетворяет неравенству

, (4.112)

то гипотеза об отсутствии автокорреляции не отклоняется (– -квантиль стандартного нормального распределения). В противном случае – в остатках наблюдается автокорреляция.

Критерий Дарбина – Уотсона. Этот критерий по сравнению с другими используется гораздо чаще. В его основу положена простая идея, в соответствии с которой, если корреляция случайной составляющей регрессии не равна 0, то она должна присутствовать и в остатках регрессии , получающихся в результате обычного МНК. В тесте Дарбина – Уотсона для оценки автокорреляции используется статистика

. (4.113)

Подробности применения этого критерия были рассмотрены в предыдущей главе. Корректное использование статистики возможно при выполнении следующих условий:

1. модель, для которой возникает необходимость применения этого критерия, должна содержать свободный член;

2. предполагается, что случайная составляющая модели 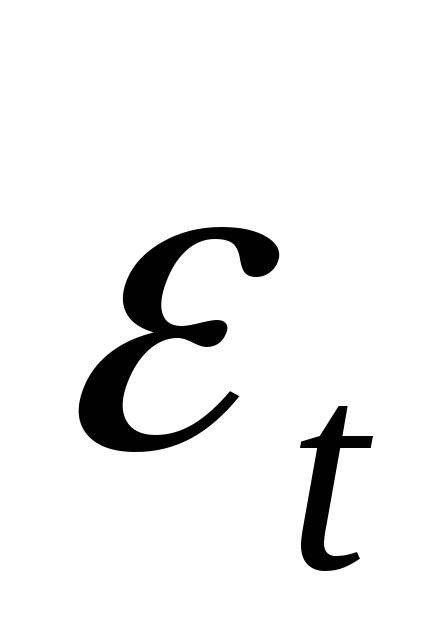определяется в соответствии с авторегрессионной схемой первого порядка;

3. наблюдения, используемые для построения модели, имеют одинаковую периодичность, т.е. в них нет пропусков;

4. критерий нельзя применять, если в регрессионной модели в число объясняющих переменных входит зависимая переменная с лагом в один период. Такое ограничение связано с тем, что распределение статистики зависит не только от числа наблюдений, но и от значений самих регрессоров. А это означает, что тест перестает выполнять роль критерия в том смысле, что нельзя указать критическую область, которая позволяла бы принимать решение об отсутствии автокорреляции в тех случаях, когда в эту область попадают наблюдаемые значения статистики .

Критерий на основе h-статистики Дарбина. Этот критерий разработан для обнаружения автокоррелированности остатков в моделях, содержащих авторегрессионные члены. Тестирование осуществляется с помощью h-статистики Дарбина, которая вычисляется по формуле

, (4.114)

где – оценка коэффициента авторегрессии;

– число наблюдений;

– выборочная дисперсия коэффициента при лаговой переменной уравнения регрессии

. (4.115)

При большом объеме выборке и справедливости нулевой гипотезы статистика h имеет стандартизованное нормальное распределение (). Это позволяет по заданному уровню значимости определить критическую точку из условия и сравнить h-статистику с . Если , то нулевая гипотеза об отсутствии автокорреляции отклоняется.

Значение рассчитывается с помощью статистики Дарбина – Уотсона по формуле

, (4.116)

а представляет собой квадрат стандартной ошибки оценки .

Таким образом, статистика h легко вычисляется на основе данных оцененной регрессии (4.115). Единственная проблема, которая может возникнуть связана с тем, что вполне возможен случай, когда .

Тест серий (Бреуша – Голдфри). Идея этого теста основана на проверки значимости коэффициента авторегрессионной модели

, (4.117)

где – остатки регрессии, коэффициенты которой получены с помощью обычного МНК.

Схема практической реализации этого теста довольно проста, и поэтому не вызывает затруднений. Преимущество теста серий перед тестом Дарбина – Уотсона в том, что он не содержит зону неопределенности. Кроме того, с помощью критерия Бреуша – Голдфри можно выявлять автокорреляцию не только между соседними, но и между отдаленными наблюдениями, т.е. проверять значимость коэффициентов в авторегрессионных моделях первого, второго и более высоких порядков

. (4.118)

Тест серий предусмотрен большинством современных компьютерных пакетов и осуществляется специальной командой.